算法与数据结构 图论（二）割点与割边

割点集合
在一个无向连通图中，如果有一个顶点集合，删除这个顶点集合，以及这个集合中所有顶点相关联的边以后，原图变成多个连通块，就称这个点集为割点集合。（一般是有多个顶点组成）
割边集合
在一个无向连通图中，如果有一个边集合，删除这个边集合以后，原图变成多个连通块，就称这个点集为割边集合。（一般有多个边组成）
点连通度
一个图的点连通度的定义为，最小割点集合中的顶点数
边连通度
一个图的边连通度的定义为，最小割边集合中的边数。
双连通图
如果一个无向连通图的点/边连通度大于1，则称该图是点/边双连通的(biconnected)，简称双连通或重连通
割点
一个图有割点，当且仅当这个图的点连通度为1，则割点集合的唯一元素被称为割点(cut point)，又叫关节点(articulation point)。
桥
一个图有桥，当且仅当这个图的边连通度为1，则割边集合的唯一元素被称为桥(bridge)，又叫关节边(articulation edge)。（也有人称为割边….）

割点：依次删除每一个顶点，然后用深度优先搜索或者广度优先搜索来检查图是否依然连通。如果删除某个顶点后，导致图不再连通，那么刚才删除的顶点就是割点。

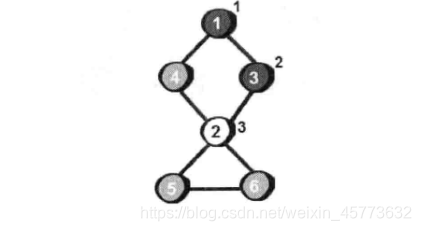
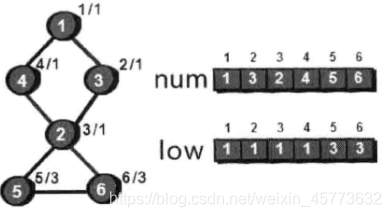
import java.util.Scanner;
//对一个图进行深度优先遍历将会得到这个图的一个生成树（并不一定是最小生成树）
public class gedian {
    static int n,m,root;
    static int [][] e = new int[9][9];
    static int [] num = new int[9];
    static int [] low = new int[9];
    static int [] flag = new int[9];
    static int index;//index用来进行时间戳的递增

    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int x,y;
        n = scan.nextInt();
        m = scan.nextInt();

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                e[i][j]=0;
            }
        }

        for (int i = 1; i <= m; i++) {
            x = scan.nextInt();
            y = scan.nextInt();
            e[x][y] = 1;
            e[y][x] = 1;
        }

        root = 1;
        dfs(1,root);

        for (int i = 1; i <= n; i++) {
            if (flag[i] == 1)
                System.out.print(i);
        }

    }

    public static void dfs(int cur,int father){//传入当前顶点编号和父顶点的编号
        int child = 0;//用来记录在生成树中当前顶点cur的儿子个数
        index++;
        num[cur] = index;//当前顶点cur的时间戳
        low[cur] = index;//当前顶点cur能访问到最早顶点的时间戳，刚开始是自己
        for (int i = 1; i <= n; i++) {//枚举与当前顶点cur有边相连的顶点i
            if (e[cur][i] == 1){
                if (num[i] == 0){//说明i点还没有被访问过，就对该点进行dfs
                    child++;
                    dfs(i,cur);

                    low[cur] = Math.min(low[cur],low[i]);//检测以cur进为父节点进行dfs时，cur是否绕过父顶点回到之前的点
                    //即，

                    if (cur != root && low[i] >= num[cur])
                        flag[cur]=1;

                    if (cur == root && child == 2)  //如果与起始点连通的点有两个，则该起始点也肯定是一个割点
                        flag[cur] = 1;
                }
                else if (i != father){//i点曾经被访问过，并且这个顶点不是当前顶点cur的父亲，则需要更新
                    //当前节点cur能否访问到更早顶点的时间戳
                    low[cur] = Math.min(low[cur],num[i]);
                }
            }
        }
    }
}

import javax.swing.*;
import java.util.Scanner;

public class gebian {
    static int n,m,root;
    static int [][] e = new int[9][9];
    static int [] num = new int[9];
    static int [] low = new int[9];
    static int index;//index用来进行时间戳的递增

    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int x,y;
        n = scan.nextInt();
        m = scan.nextInt();

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                e[i][j]=0;
            }
        }

        for (int i = 1; i <= m; i++) {
            x = scan.nextInt();
            y = scan.nextInt();
            e[x][y] = 1;
            e[y][x] = 1;
        }

        root = 1;
        dfs(1,root);

    }


    public static void dfs(int cur,int father){//传入当前顶点编号和父顶点的编号
        int child = 0;//用来记录在生成树中当前顶点cur的儿子个数

        index++;
        num[cur] = index;//当前顶点cur的时间戳
        low[cur] = index;//当前顶点cur能访问到最早顶点的时间戳，刚开始是自己
        for (int i = 1; i <= n; i++) {//枚举与当前顶点cur有边相连的顶点i
            if (e[cur][i] == 1){
                if (num[i] == 0){//说明i点还没有被访问过，就对该点进行dfs
                    child++;
                    dfs(i,cur);

                    low[cur] = Math.min(low[cur],low[i]);//检测对cur进行dfs时，cur是否绕过父顶点回到之前的点
                    if (low[i] > num[cur])//low[i]>=num[cur]表示的是点i不可能在不经过父节点u而回到祖先(包括父亲)的，
                        //而low[i] > num[cur]表示连父亲都回不到了。倘若顶点i不能回到祖先，也没有另外一条路能回到父亲，那么
                        //i-cur这条边就是割边
                        System.out.println(String.format("%d-%d",cur,i));
                }
                else if (i != father){//i点曾经被访问过，并且这个顶点不是当前顶点cur的父亲，则需要更新
                    //当前节点cur能否访问到更早顶点的时间戳
                    low[cur] = Math.min(low[cur],num[i]);
                }
            }
        }
    }
}