连通图、强连通图

连通图、强连通图
图中从一个顶点到达另一顶点，若存在至少一条路径，则称这两个顶点是连通着的。
例如图 1 中，虽然 V1 和 V3 没有直接关联，但从 V1 到 V3 存在两条路径，分别是 V1-V2-V3 和 V1-V4-V3，因此称 V1 和 V3 之间是连通的。

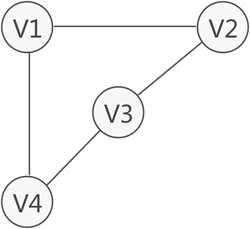
图 1 顶点之间的连通状态示意图

连通图

无向图中，如果任意两个顶点之间都能够连通，则称此无向图为连通图。例如，图 2 中的无向图就是一个连通图，因为此图中任意两顶点之间都是连通的。

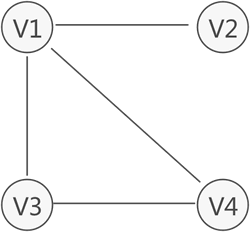
图 2 连通图示意图

连通分量
若无向图不是连通图，但图中存储某个子图符合连通图的性质，则称该子图为连通分量

最大子图 极大连通子图
图中部分顶点和边构成的图为该图的一个子图，但这里的子图指的是图中"最大"的连通子图（也称"极大连通子图"）

如图 3 所示，虽然图 3a) 中的无向图不是连通图，但可以将其分解为 3 个"最大子图"（图 3b)），它们都满足连通图的性质，因此都是连通分量

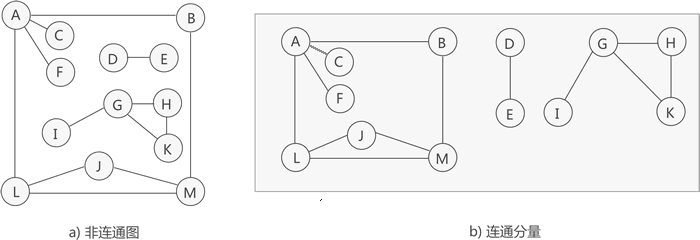
图 3 连通分量示意图

提示 图 3a) 中的无向图只能分解为 3 部分各自连通的"最大子图"。
要注意的是，连通分量的提出是以"整个无向图不是连通图"为前提的，因为如果无向图是连通图，则其无法分解出多个最大连通子图，因为图中所有的顶点之间都是连通的

强连通图
有向图中，若任意两个顶点 \(V_i\) 和 \(V_j\)，满足从 \(V_i\)到 \(V_j\)以及从 \(V_j\)到 \(V_i\) 都连通，也就是都含有至少一条通路，则称此有向图为强连通图。
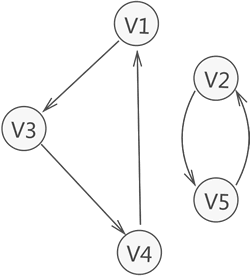
如图 4 所示就是一个强连通图

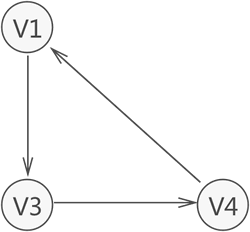
强连通分量
若有向图本身不是强连通图，但其包含的最大连通子图具有强连通图的性质，则称该子图为强连通分量

可以这样说，连通图是在无向图的基础上对图中顶点之间的连通做了更高的要求，而强连通图是在有向图的基础上对图中顶点的连通做了更高的要求