排列组合-球盒问题

排列组合-球盒问题
1 球相同，盒子相同，盒子不能空
例1
8个相同的球放入3个相同的盒子中，每个盒子中至少有一个. 问有多少种不同的放法？ 5
球入盒问题，可以看成分两步完成，首先是将8个球分成三堆，每堆至少一个. 
由于这里球和盒子都相同，每三堆放入3个盒子中只有一种情况，所以只要将8个球分成三堆. 
即1-1-6、1-2-5、1-3-4、2-2-4、2-3-3 共5种

结论 ｎ个相同的球放入ｍ个相同的盒子（n≥m），不能有空盒时的放法种数等于ｎ分解为ｍ个数的和的种数

2.球相同，盒子相同，盒子可以空
例2
8个相同的球放入3个相同的盒子中. 问有多少种不同的放法？
此题和例1类似，盒子可以为空，所以分放入1个盒子，放入2个盒子，放入3个盒子三种
放入1个盒子 1种
放入2个盒子 1-7 2-6 3-5 4-4 共4种
放入3个盒子，即为例1的情况，共5中
所以总方案数为1+4+5=10种

结论 ｎ个相同的球放入ｍ个相同的盒子（n≥m），可以有空盒时的放法种数等于将ｎ分解为ｍ个、(ｍ－1)个、(ｍ－2)个、…、2个、1个数的和的所有种数之和

3.球相同，盒子不同，盒子不能空 -隔板法
例3
8个相同的球放入标号为1、2、3的三个盒子中，每个盒子中至少有一个. 问有多少种不同的放法？
C(m-1,n-1)=C(7,2)=7*6/2=21

结论  ｎ个相同的球放入ｍ个不同的盒子中（n≥m），不能有空盒的放法数 C(n-1,m-1)

4.球相同，盒子不同，盒子可以空  -隔板法变形
例4
8个相同的球放入标号为1、2、3的三个盒子中. 问有多少种不同的放法？
盒子可以为空，转化为盒子不能为空的情况，通过每个盒子放入一个球转化
转化需借用3个球放入，此时总球数为8+3=11
所以C(m-1,n-1)=C(10,2)=45

结论  ｎ个相同的球放入ｍ个不同的盒子中（n≥m），可以有空盒的放法数 C(n+m-1,m-1)

5.球不同，盒同，盒子不能空 -第二类斯特林数
例5
8个不相同的球放入3个相同的盒子中，每个盒子中至少有一个. 问有多少种不同的放法？
S(n,m)=S(8,3)=966
根据第二类斯特林三角

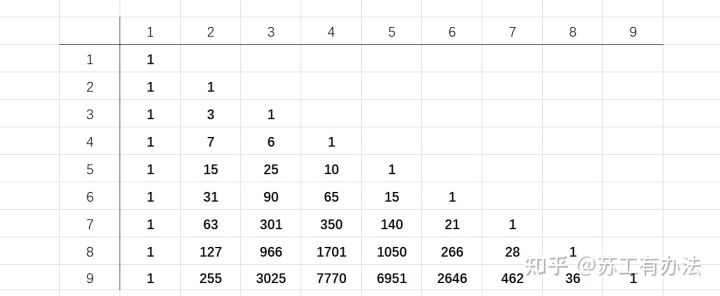
性质1，左右两边都是1，第几行就有几个数，比如第 5 行就是 1 X X X 1。

性质2，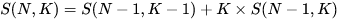
，含义是第N排的第K个数等于 { 它上一排的左上角位置的数字 } 加 { 它上一排的同样位置数字的K倍}。

6.球不同，盒同，盒子可以空 -第二类斯特林数变形
例6
8个不相同的球放入3个相同的盒子中， 问有多少种不同的放法？
盒子可以为空，因此可以分8个不同的球放入3个相同的盒子、放入2个相同的盒子、放入1个相同的盒子三种情况
所以总方案数为：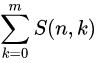

S(8,3) + S(8,2) + S(8,1)=966 + 127 + 1=1094

7.球不同，盒不同，盒子不能空 -第二类斯特林数变形
盒子有区别，所以在5的基础上乘上盒子的排列即可

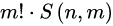
例7
8个不相同的球放入标号为1、2、3的三个盒子中，每个盒子中至少有一个. 问有多少种不同的放法？
A(m,m) * S(n,m)=m! * S(n,m)=3! * S(8,3)=6 * 966=5796

8.球不同，盒不同，盒子可以空 -第二类斯特林数变形
枚举非空盒子的数目，另外盒子有区别需要乘以排列数

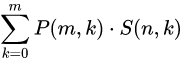
例8
8个不相同的球放入标号为1、2、3的三个盒子中，问有多少种不同的放法？
盒子可以为空因此可以分8个不同的球放入3个不同的盒子、2个不同的盒子、1个盒子
A(3,3) * S(8,3) + A(3,2) * S(8,2) + A(3,1) * S(8,1)=6 * 966 + 6 * 127 + 3 * 1=5796 + 762 + 3=6551

方案2
允许盒子为空，且盒子间有区别，那么对于每个球有m种选择，每个球相互独立。有方案数：\(m^n=3^8=6561\)