NOIP初赛复习（十三）计算几何基础

计算几何（Computational Geometry），即以计算为主的几何。主要研究几何形体的计算机表示、分析与综合。计算几何在数字可视化、图形学、辅助设计、机器人、地理信息、集成电路、计算机视觉等领域被广泛使用。

1、点

 

 

 

 

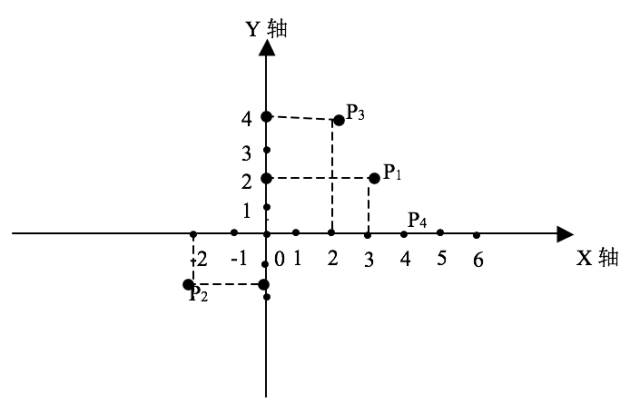
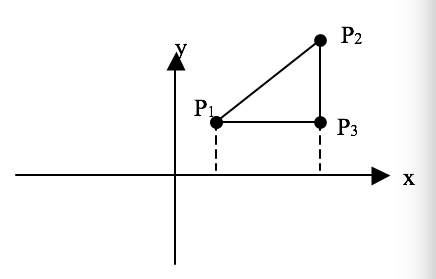
点一般表示成P(x,y)，其中x,y为点的坐标。如上图4个点的坐标分别为：

P₁(3,2)  P₂(-2,-2)  P₃(2,4)  P₄(4,0)。

过两点可连成一线段，两点之间的距离记为：

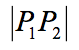
假设点的坐标为：

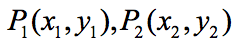
由勾股定理可知：

 

 

 

 

 

 

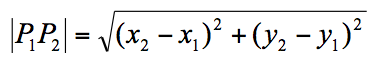
例如：

 

 

 

 

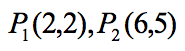
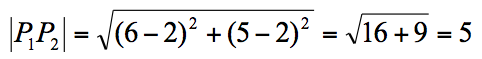
2、直线

直线的方程：

一般形式为：ax+by+c=0，或y=kx+b。k称为直线的斜率，b称为截矩。

 

 

 

 

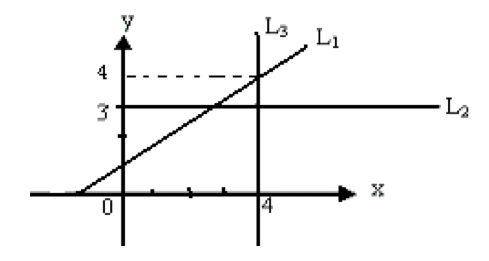
如上图中，直线L₁的方程为：0.75x-y+1=0，L₂：y=3，L₃：x=4。

直线的斜率：

如上图中，直线L₁的斜率为0.75。

特别地：当y₁=y₂时，斜率k=0(如上图中的L₂)，

当 x₁=x₂时，k不存在(如上图中的L₃)。

 

 

 

 

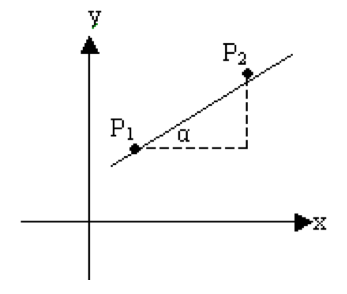
过两点P₁，P₂可以决定一条直线。斜率为：

 

 

 

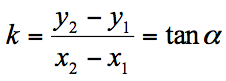
而当x₁与x₂无限接近时，斜率k趋于无穷大，这在编程时要特别小心。

 

3、向量（矢量）

简单的说，向量（vector）就是有大小有方向的量，如速度、位移等物理量都是向量。

如：有方向的线段，即P1和P2的顺序是有关系的，记为：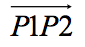

 

 

 

如果P1是坐标原点，则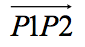又称为向量P2，如下面示意图。

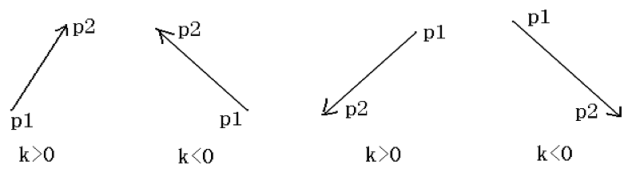
向量的斜率：既然向量是有方向的，那么向量的斜率k就是有正负之分的，具体如下：

 

 

 

 

 

设 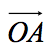   =a，则有向线段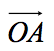的长度叫做向量a的长度或模。记作|a|。

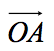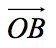夹角：两个非0向量a、b，在空间任取一点O，作=a， =b，则角∠AOB叫做向量a与b的夹角，记作<a，b>。若<a，b>=π/2，则称a与b互相垂直，记作a⊥b。

 

4、向量的加减法

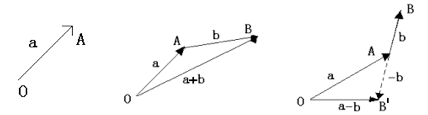
以点O为起点、A为端点作向量a，以点A为起点、B为端点作向量b，则以点O为起点、B为端点的向量称为a与b的和a+b，如下中图。

若从A点作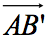 ，要求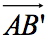的模等于|b|，方向与b相反，即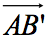=-b，则以O为起点、B’为端点的向量称为a与b的差a-b，如下右图。

 

 

 

5、向量的数量积（点乘）

两个向量的数量积是一个数，大小等于这两个向量的模的乘积再乘以它们夹角的余弦。

a·b＝|a||b|cos<a,b>

用上面讲到的向量的分解可以证明，数量积等于两个向量的对应支量乘积之和。

a·b＝a_xb_x＋a_yb_y＋a_zb_z

数量积的性质：

a·e=|a||e|cos<a,e>=|a|cos<a,e>

a⊥b 等价于 a·b＝0,即a_xb_x＋a_yb_y＋a_zb_z=0

自乘：|a|² ＝ a·a

结合律：（λ·a）·b = λ(a·b)

交换律：a·b ＝ b·a

分配律：a·(b + c) ＝ a·b + a·c

6、向量的向量积（叉乘、叉积）

向量积的一般含义：两个向量a和b的向量积是一个向量，记作a×b，其模等于由a和b作成的平行四边形的面积，方向与平行四边形所在平面垂直，当站在这个方向观察时，a逆时针转过一个小于π的角到达b的方向。这个方向也可以用物理上的右手螺旋定则判断：右手四指弯向由A转到B的方向（转过的角小于π），拇指指向的就是向量积的方向。如下左图。

 

 

 

 

 

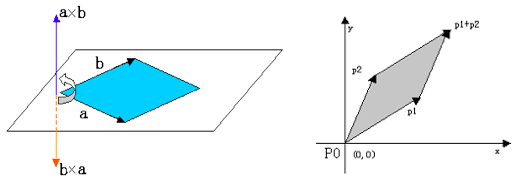
我们给出叉积的等价而更有用的定义，把叉积定义为一个矩阵的行列式：

 

 

 

 

 

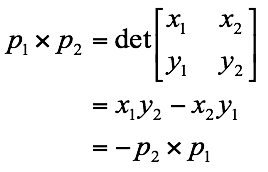
如上右图，如果为正数，则相对原点(0,0)来说，在的顺时针方向；如果为负数，则在的逆时针方向。如果=0，则和模相等且共线，方向相同或相反。

也可以用向量的分解证明：

 

即: 

注：i,j,k分别为x,y,z方向上的单位向量

现在探讨一个重要的问题：给定两个向量：和 ，对它们的公共端点P0来说，判断是否在的顺时针方向。

 

方法：如上图，把P0作为原点，得出向量P1’=P1-P0和P2’=P2-P0，因此，这两个向量的叉积为：

如果该叉积为正，则在的顺时针方向，如果为负，则在的逆时针方向。如果等于0，则P0，P1，P2三点共线。

讨论另一个重要问题：确定连续线段是向左转还是向右转，如下图，即两条连续线段和在点P1是向左转还是向右转。也即∠P₁P₀P₂的转向。

 

方法：叉积，同上。

向量的叉积对于计算几何有着重要的意义，是很多算法的核心。用叉积可以判断从一个向量到另一个向量的旋转方向，可以求同时垂直于两个向量的直线（向量）方向，还能用来计算面积……。

向量的旋转：实际应用中，经常需要从一个向量转到另一个向量，这个过程称为向量的旋转，旋转的方向由叉积判定。很多例子都用到向量的旋转这个方法和相应特性。