排列组合

排列组合“分组分配问题”始终不懂？讲给你本质
https://www.bilibili.com/video/BV1Pi4y1K7rM?spm_id_from=333.337.search-card.all.click

组合数问题
https://www.luogu.com.cn/problem/P2822

排列组合

排列

从n个不同元素中,任取m个元素,按照一定的顺序排成一 列,叫做从n个不同元素中取出m个元素的一个排列

排列公式

\(A^m_n = n * (n-1) * (n-2) ... (n-m+1) = \frac{n!}{(n-m)!}\)

全排列

n个不同的元素排成一排，排列方法有

\(A^n_n = n * (n-1) * (n-2) ... 2 * 1 = n!\)

组合

从n个不同元素中,任取m个元素,并成一组,叫做从n个 不同元素中取出m个元素的一个组合

组合数公式

\(C^m_n= \frac{A^m_n}{A^m_m}= \frac {n * (n-1) * (n-2) ... (n-m+1)}{m!}\)

排列与组合的区别与联系:与顺序有关的为排列问题,与顺序 无关的为组合问题

例1

学校师生合影，共8个学生，4个老师，要 求老师在学生中间，且老师互不相邻，共有多 少种不同的合影方式？

例2

5个男生3个女生排成一排,3个女生要排在一起, 有多少种不同的排法?

例3

袋中有不同年份生产的5分硬币23个, 不同年份生产的1角硬币10个,如果从袋中取出2元钱,有多少种取法?

例4

学校安排考试科目9门,语文要在数学之前考,有多少种不同的安排顺序?

例5

某个班级共有43位同学,从中任抽5人,正、副班长、团支部书记至少有一人在内的抽法有多少种?

例6

（NOIP7）平面上有三条平行直线，每条直线上分别有7， 5，6个点，且不同直线上三个点都不在同一条直线上。 问用这些点为顶点，能组成多少个不同三边形？

例7

（NOIP10）由3个a，5个b和2个c构成的所有字符串中， 包含子串“abc”的共有（ ）个

例8

NOIP2014(提高组） 同时查找2n个数中的 最大值和最小值，最少比较次数为( )

例9

“IMO”是国际数学奥林匹克的缩写，把这 3 个字母用 3 种不同颜色来写，现有 5 种不同颜色的笔，问共有多少种不同的写法？

例10

⑴6 个人走进有 10 辆不同颜色碰碰车的游乐场，每辆碰碰车只能坐一个人，那么共有多少种不同的坐法？

⑵某条铁路线上，包括起点和终点在内原来共有 7 个车站，现在新增 3 个车站，铁路上两站 之间往返的车票不同，则这样需要增加多少种不同的车票？

例11

书架上有 3 本不同的故事书，2 本不同的作文选和 1 本漫画书，全部竖起来排成一排。
⑴如果同类的书可以分开，一共有多种排法？
⑵如果同类的书不可以分开，一共有多少种排法？

例12

用 1、2、3、4、5 这五个数字，不许重复，位数不限，能写出多少个 3 的倍数？

例13

一共有红、橙、黄、绿、青、蓝、紫七种颜色的灯各一盏，按照下列条件把灯串成一串，有多少种不同的串法？
⑴把 7 盏灯都串起来，其中紫灯不排在第一位，也不排在第七位。
⑵串起其中 4 盏灯，紫灯不排在第一位，也不排在第四位。

例14

八个同学照相，分别求出在下列条件下各有多少种站法？
⑴八个人站成一排；
⑵八个人排成一排，某两人必须有一人站在排头；
⑶八个人排成一排，某两人必须站在两头；
⑷八个人排成一排，某两人不能站在两头。

例15

四年级三班举行六一儿童节联欢活动，整个活动由 2 个舞蹈、2 个演唱和 3 个小品组成。
请问：
⑴如果要求同类型的节目连续演出，那么共有多少种不同的出场顺序？
⑵如果要求 3 个小品分开演出，那么共有多少种不同的出场顺序？

例16

七个人排成一排，分别求出在下列条件下各有多少种站法。
⑴七个人排成一排，前排三人，后排四人，某两人不在同一排；
⑵甲、乙、丙两两不相邻的不同排法有（ ）种；
⑶甲乙丙三人必须挨着的不同排法有（ ）种；
⑷甲不站在左端，乙不站在右端的不同排法有（ ）种。

例17

有 3 名男生，4 名女生，在下列不同要求下，求不同的排列方法总数。
⑴全体排成一行，其中甲只能在中间或者两边位置；
⑵全体排成一行，其中甲不在最左边和最右边；
⑶全体排成一行，其中男生必须排在一起；
⑷全体排成一行，男、女各不相邻；
⑸全体排成一行，男生不能排在一起；
⑹全体排成一行，其中甲、乙两人从左至右的顺序不变。

例18

由 0，2，5，6，7，8 组成无重复数字的数。
⑴由小到大排列的四位数中，5607 是第几个数？
⑵由小到大排列的四位数中，第 128 个数是多少？

例19

由 0，2，4，5，7，8 组成无重复数字的数。
⑴五位数有多少个？
⑵五位奇数有多少个？
⑶五位偶数有多少个？
⑷自然数有多少个？
⑸是 5 的倍数的三位数有多少个？
⑹是 25 的倍数的四位数有多少个？

例20

有 10 名同学
⑴从中选两个人排成一排照相，有多少种不同的方法？
⑵从中选两个人参加节目，有多少种不同的方法？

例21

⑴9 支球队进行足球比赛，实行单循环制(每两队之间比赛一场)，那么一共要举行( )
场比赛；若进行双循环制(有主客场之分)，则一共要举行( )场比赛。
⑵体育课上，老师从 10 名男生中挑出 4 人去抬体育器材，一共有多少种不同的方法？
⑶学校开设 6 门任意选修课，要求每个学生从中选学 3 门，共有多少种不同的选法

例22

美国篮球职业联赛(NBA)总决赛在洛杉矶湖人队和波士顿凯尔特人队之间进行，比赛采用 7 场 4 胜制，即先获得 4 场胜利的球队将得到总冠军。比赛分为主场和客场，由于洛杉矶湖人队常规赛战绩较好，所以第 1，第 2，第
6，第 7 场均在洛杉矶进行，第 3—5 场在波士顿进行。最后湖人队在自己的主场获得总冠军，那么比赛过程中的胜负结果共有( )种可能

例23

⑴大海老师把 10 张不同的游戏卡片分给佳佳和阳阳，并且决定给佳佳 8 张，给阳阳 2 张。一共有多少种不同的分法？
⑵8 名学生和 6 名老师分成红、蓝两队拔河，要求每个队都是 4 名学生和 3名老师，一共有多少种分队的方法？

例24

在一次合唱比赛中，有身高互不相同的 8 个人要站成两排，每排 4 个人，且前后对齐。而且第二排的每个人都要比他身前的那个人高，这样才不会被挡住。一共有多少种不同的排队方法？

例25

⑴在一个圆周上有 10 个点，那么以这些点为顶点或端点，可以画出( )条线段；( )个三角形；( )个四边形。
⑵如图，在半圆弧及其直径上共有 9 个点，以这 些点为顶点可画出多少个三角形

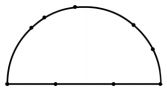
例26

一个小组共 10 名学生，其中 5 女生，5 男生。现从中选出 3 名代表，其中至少有一名女生的选法？

例27

用 2，4，6 三个数字来构造六位数，但是不允许有两个连着的 2 出现在六位数中(例如 626442 是允许的，但 226426 就不允许)，问这样的六位数有多少个？

例28

⑴如果一个大于 9 的整数，其每个数位上的数字都比它右边数位上的数字小，那么我们称它为“迎春数”。那么，小于 2008 的“迎春数”共有( )个

⑵某种奖券的号码有 6 位，如果奖券至少有两个非零数字并且从左边第一个非零数字起，每个数字小于它右边的数字，就称这样的号码为“中奖号码”，如 000015，001257。“中奖号码”有多少个？

例29

某旅社有导游 9 人，其中 3 人只会英语，2 人只会日语，其余 4 个既会英语又会日语。现要从中选 6 人，其中 3 人做英语导游，另外 3 人做日语导游。则不同的选择方法有多少种?

例30

从 1~25 这 25 个自然数中，每次取出两个不同的数，使它们的和是 4的倍数，共有( )种不同的取法

例31

⑴把 10 个相同的球放入 3 个不同的盒子里，要求每个盒子里至少有一个球，有多少种放法？
⑵佳佳有 10 块糖，每天至少吃 1 块，5 天吃完，她共有多少种不同的吃法？

⑶一个电视台播放一部 12 集的电视剧，要分 5 天播完，每天至少播一集，有多少种不同的方法？

例32

⑴把 12 个相同的球放入 3 个不同的盒子里，要求每个盒子里都至少有2 个球，有多少种放法？
⑵光明小学甲、乙、丙两个班组织了一次文艺晚会，共演出十四个节目。如果每个班至少演出三个节目，那么，这三个班演出节目数的不同情况共有多少种?

例33

六个人排成一排照相，
⑴若小明必须与小丽排在一起，有多少种排法？
⑵若小明和小丽不能排在一起，有多少种排法？

例34

正六边形的中心和顶点共 7 个点，以其中 3 个点为顶点的三角形共有多少个？

例35

在新学期的班会上，大家从 11 名候选人中选出班干部。请问：

⑴选出三人组成班委会，那一共有多少种选法？
⑵从剩下的候选人中，选出三人分别担任语文、数学、英语的课代表，一共有多少种选法？

例36

从 15 名同学选出 5 人，上场参加篮球比赛。
请问：
⑴如果甲、乙、丙三人中恰好入选一人，共有多少种选法？
⑵如果甲、乙、丙不能同时都入选，共有多少种选法？

例37

⑴在图中 1×5 的格子中填入 1，2，3，4，5 这 5 个数，要求，填入的数各不相同并且填在黑格里的数比它旁边的两个数都大。共有()种不同的填法。

⑵在图中 1×5 的格子中填入 1，2，3，4，5，6，7，8 中的 5 个数，要求，填入的数各不相同并且填在黑格里的数比它旁边的两个数都大。共有( )种不同的填法。

例38

从 10 名男生，8 名女生中选出 8 人参加游泳比赛。在下列条件下，分别有多少种选法？
⑴恰有 3 名女生入选；
⑵至少有两名女生入选；
⑶某两名女生，某两名男生必须入选；
⑷某两名女生，某两名男生不能同时入选；
⑸某两名女生，某两名男生最多入选两人。

例39

A、B、C、D、E 五种不同的商品要在货架上排成一排，其中 A、B 两种商 品必须排在一起，而 C、D 两种商品不能排在一起，则不同的排法共有多少种？

例40

某博物馆要在 10 天内接待 4 所学校的学生参观，每天至多安排一所学校，其中一所人数较多的学校要连续参观 2 天，其余学校均只参观 1天，则在这 10 天内不同的安排方法数是多少种？

例41

如图，A、B、C、D 为海上的四个小岛，要建三座桥，将这四个岛连接起来，则不同的建桥方案共有( )种。

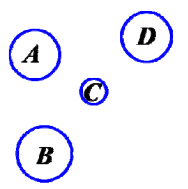
例42

把 10 个相同的球放入 3 个不同的盒子里，若要求⑴每个盒子里至少有一个球，有多少种放法？
⑵每个盒子里都至少有 2 个球，有多少种放法？
⑶某些盒子允许空着，有多少种放法？

例43

⑴方程 x＋y＋z＝13 有多少组正整数解？
⑵方程 x＋y＋z＝13 有多少组非负整数解？
⑶方程 x＋y＋z＝13 有多少组 x，y，z 均不小于 2 的正整数解？

例44

14 个相同的小球放入编号为 1，2，3 的三个盒子内，要求每个盒子的球数不小于它的编号数，

则不同的放法共有( )种。

例45

在四位数中，各位数字之和是 4 的四位数有多少？