CSP-J 2020 入门组初赛第一轮初赛试题答案及解析

         CSP-J 2020 入门组初赛第一轮初赛试题

         https://www.cnblogs.com/myeln/articles/14998653.html

         http://www.doc88.com/p-07647122296829.html

 

1. A
2. A
3. D 解析 : 与z与的都是假
4. C 解析 : 2048*1024*32/8=2048*1024*4=1024*1024*8=8MB
5. C 解析 : 序列有序的情况  https://visualgo.net/zh/sorting 

   冒泡排序是一种交换排序， 它的思路是：
   两两比较相邻记录的数值， 如果与序列不符则交换
   数值， 持续访问记录直到没有反序的情况为止。 如
   果序列原本即呈现有序状态， 则只需比较 n-1 次就
   好（即一轮完成）。

6. B 返回最小值
7. A 解析 : 链表访问元素是 O(n)的 数组可随机访问
8. A

   图（graph） 是一种描述多对多关系的数
   如果给图的每条边规定一个方向， 则我
   们将这样的图称为有向图， 反之则称为无向图。 如
   果图中任意两点都是连通的， 则图被称作连通图。
   例如， 图 2 无向图有 5 个顶点， 则至少应该有 4 条
   边才能确保是一个连通图

9. A  1 × 2 ³ + 0 × 2 ² + 1 × 2 ¹ + 1 × 2 ⁰ = 11
10. A 解析 : 将双胞胎看成一个人，总方案为 A44, 双胞胎内部有序，故答案为A44×A22=48
    
11. A 

    先将双胞胎看作整体， 则总方案数为A 44
    再观察双胞胎的左右状态， 这个状态也是有序的，
    最后根据乘法原理答案为A 44× A 22= 48

12. D 解析 ： ⌈log2⁶¹⌉=6 或者2ⁿ-1求二叉树最大节点数综合判断
13. C 

    依题意模拟并与表对照即可
    1949 % 10 = 9， 对应汉字己
    1949 % 12 = 5， 对应汉字丑

14. A 解析 ：插板法  C(n-1)(m-1)  C96=84
    
15. A 解析 ：任意取出两幅 C52 需要取6只手套，目前只取了4只，还没完成，还需要在剩余里面再取2只 C62 ( C62 中包含可以组成一幅手套的情况为C31  ), 总方案 C52×(C62−C31)=10*(15-3)=120

2阅读程序

1. TFTF AD

   代码大意 : 将CSP分别对应ABC,其余顺延

   解析 ：

   1. 仅大写字母下标会在范围内
   2. T-Z均相同
   3. i<=3i<=3即可
   4. 预处理要处理所有26个字母
   5. 模拟即可
   6. 模拟即可

   具体对应如图所示
   

2. FFT DBD

   代码大意 : 求将一个数字n转化成k进制数的总进位次数

   解析 ：

   1. 简单模拟后可以发现之后所有都加到了第二位,输出时len为2
   2. 考虑n等于1的情况
   3. 等于就会向前进位,所以一定是大于的
   4. 当k为1时,每一次都会统计答案,答案即为n
   5. 从前往后第i位共进位3(i−1)3(i−1) 次,故答案为$ 3⁰⁺³1+......+3^{30} $,等比数列求和即可
   6. 当k等于10时,即十进制,不断对10取模并加到答案即可

3. FTF BCC

   代码大意 : 给定两个数列，每次操作可以选择相同位置的两个数相加形成一个新的数，每次相加造成的价值为1数列两数之和与2数列两数之差，求合并n-1次后的最大价值。

   解析 ：

   1. n为0时会直接结束循环
   2. 若都为0，合并后结果也是0
   3. 反例 ：2 1 1 10000 10000
   4. 等差数列暴力计算即可 ：20个9从前往后合并，答案加上每次合并后的值
   5. 等差数列暴力计算即可，从前往后合并，答案每次加上两数之差
   6. 容易猜到证明贪心的从前往后选，暴力计算即可

3完善程序

　　　　　　1.CCCAC

　　　　　　  1.最小的质因子从 2 开始
　　　　　　  2.只需要枚举至 n−−√n 即可
　　　　　　  3.考虑多个相同质因子情况
　　　　　　  4.若n本身为质数需要特判或有比n−−√n 更大的因数
　　　　　　　　特判后输出

                       2.BDAAB

                          1.冒泡排序，根据题意，应该以线段左端点为关键字排序

                          2.交换变量

                          3.去掉覆盖重复线段,使得线段右端点保证递增,如下图所示：b线段已经覆盖了c线段，所以c线段被舍去

　　　　　　　   

 

 

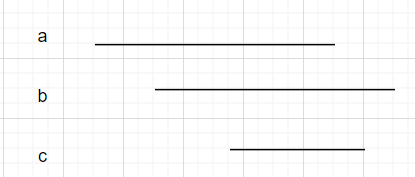
                          4.去除一些对覆盖不起关键作用的字段，比如下图b线段,可以覆盖的情况，a和b已经包括了b

　　　　　　　　程序实现方法:

　　                      针对加入的最后一个线段的右端点，假设最后一个线段temp 最后一个线段右端点temp.r  找到>temp.r的线段A[q+1]

                             通过q记录下一个要加入的线段，如果线段有A[q+1].a<=r  (已经加入的字段)  说明有重合，继续找，知道找到A[q+1].a>r

                              则A[q]就是最后一个可以加入的字段

                             

 

 

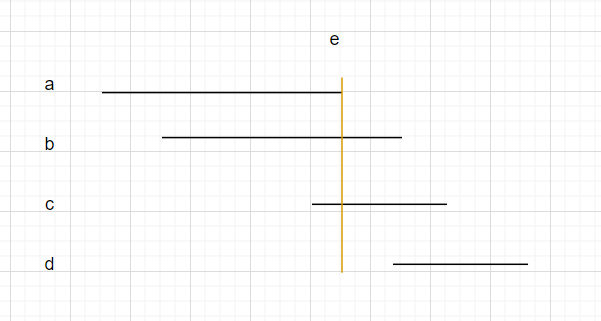
                          5.更新右端点

                           使用加入线段的右端点，更新此时加入所有线段的最右端点