CSP普及赛初赛质数

CSP普及赛初赛质数

称一个数为质数当且仅当这个数的质因子只有 1 和他本身

1.1 不是质数

2.2是最小的质数,也是唯一一个同时是偶数也是质数的数

质数判断

试除法

bool isPrime(int k) {
 if(k < 2)
     return false;

 for(int i = 2; i <= k / i; i++) {
  if(k % i == 0) {
   return false;
  }
    }
 return true;
}

质数筛法

在所有大于 0 的自然数中, 除了质数就是合数. 要求质数, 只需要 "筛" 去所有的合数即可.

筛去合数要比依次判断每个数是否时质数要快的多

朴素筛法 - 埃氏筛法 时间复杂度 O(n*logn)

https://blog.csdn.net/Gavin_Nicholas/article/details/88974079

 

 

 

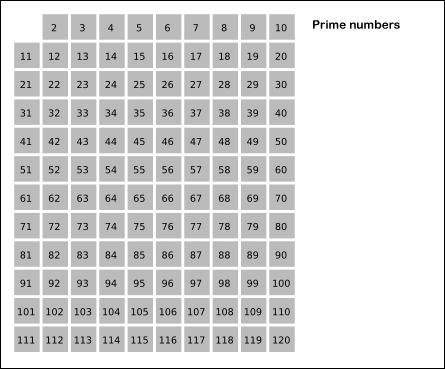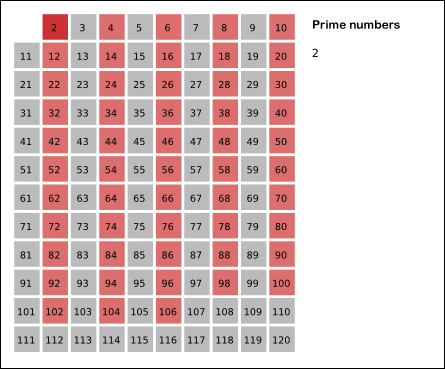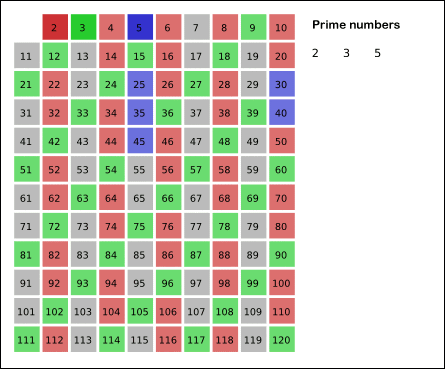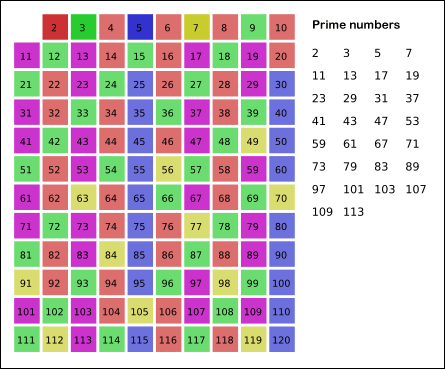
线性筛 - 欧拉筛

时间复杂度接近O(n)

欧拉筛法的基本思想 ：在埃氏筛法的基础上，让每个合数只被它的最小质因子筛选一次，以达到不重复的目的

• 所有合数都要筛到
• 不能有重复筛选, 否则无法达到在线性时间内的运行

 

P3383 【模板】线性筛素数

https://www.luogu.com.cn/problem/P3383

埃氏筛法-埃拉托斯特尼筛法

#include <bits/stdc++.h>
using namespace std;
const int N = 1e8 + 8;
int p[N], cnt = 0;
bool st[N];
int n, q;
void get_primes(int n){
    for(int i=2;i<=n;i++){
        if(st[i])
            continue;
        p[++cnt] = i;
        for(int j=i+i;j<=n;j+=i){
            st[j]=1;
        }
    }
}
int main(){
    scanf("%d %d", &n, &q);
    get_primes(n);
    int x;
    while(q--){
        scanf("%d", &x);
        printf("%d\n", p[x]);
    }
    return 0;
}

 

线性筛 - 欧拉筛

#include <bits/stdc++.h>
using namespace std;
const int N = 1e8 + 8;
//p质数数组p 欧拉筛法核心 每个合数只被最小的质数筛掉 
int p[N], cnt = 0;
bool st[N];//false 可以加入质数，设置为true后不能添加 
int n, q;
void get_primes(int n){
    for(int i=2; i<=n;i++){
        if(st[i] == 0)//从小到大 没被筛掉(说明是质数) 则添加 
            p[++cnt] = i;
        /*
        使用最小的质数 筛掉对应合数
        i=2 筛掉 4              2
        i=3 筛掉 6  9           2 3
        i=4 筛掉 8              2 3
        i=5 筛掉 10 15 25       2 3 5
        i=6 筛掉 12             2 3 5 
        i=7 筛掉 14 21 35       2 3 5 7
        i=8 筛掉 16             2 3 5 7 
        i=11筛掉 22 33 55 77    2 3 5 11 
        i=12筛掉 24             2 3 5 11 
        */
        /*
        i*p[j]筛掉的合数需要<=n  j继续++没意义 超出筛掉合数范围 
        保证使用最小质数筛掉合数 
        i%p[j]==0 最小质数 筛掉合数后break  由于p[j] 随j逐渐增大 
        */ 
        for(int j=1;i*p[j]<=n;j++){//筛掉的数在找的素数范围 否则计算无意义 
            st[i*p[j]]=1;//筛掉i*p[j]这个合数 i>p[j] p[j]为最小质数 
            /*
            保证使用最小质数筛
            i%p[j]!=0说明p[j]还没找到最小质数 继续j++
            i%p[j]==0说明p[j]已经找最小质数 break 
            */
            if(i%p[j]==0)  
                break;
        }
    }
}
int main(){
    scanf("%d %d", &n, &q);
    get_primes(n);
    int x;
    while(q--){
        scanf("%d", &x);
        printf("%d\n", p[x]);
    }
    return 0;
}