字符串

模式匹配

• KMP
  思想:
  当匹配到模式串p第j个元素 p0[j]!=p[i]
  可知p0(j-h,j-h+1,j-h+2...j-1)与p(i-h,i-h+1..i-1)相同
  由于根据模式串自身前后缀性质 显然当模式串滑动1,2...个元素时不可能与自身匹配成功 也就不能与目标串匹配成功
  故要找出最大滑动距离

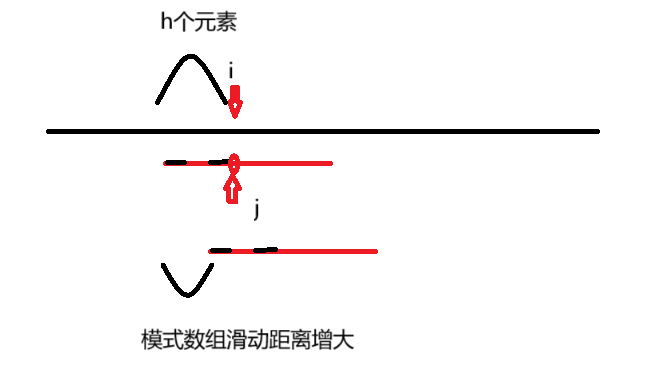
缩小的范围可根据F数组迭代求解

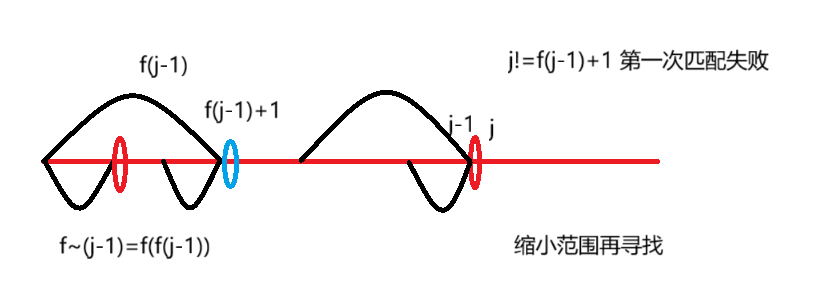
int strStr(string haystack, string needle) {
	int n = haystack.size();
	int m = needle.size();
	vector <int> f(m);
	for (int i = 0; i < m - 1; i++) {
		f[i] = -1;
	}
	
	for (int i = 0; i < m - 1; i++)   //预处理F数组 找到最大滑动距离
	{
		int j = f[i];
		while (needle[i + 1] != needle[j + 1] && j >= 0) {//寻找相同前后缀范围
			j = f[j];   //缩小范围
		}
		if (needle[i + 1] == needle[j + 1]&&j>=0)f[i + 1] = j + 1;     //前缀为0~j+1    错误写法:f[i + 1] = f[j] + 1;
		else if(needle[i + 1] == needle[j + 1] && j == -1)f[i + 1] = 0;//前缀为第一个元素
		else f[i+1] = -1;                                              //无匹配前缀
	}
	int i = 0, j = 0;              //匹配开始
	                               //因i j均不倒退 故直接更新i j 而不是用辅助元素k i~i+k j~j+k
	while (i<n&&j<m) {
		if (needle[j] == haystack[i]) {
			 
			if (j == m - 1)return i-m+1;
			i = i + 1;
			j = j + 1;
		}
		else{
			 
				if (j == 0) i = i + 1;//若从模式串第一个元素就不匹配 则移动目标串指针
				else j = f[j-1] + 1;  
         /*
              错误写法:
               if (f[j] == -1) {
				j = 0;
               }
               else {
				j = f[j];
               }
         */
			 
		}
	}
	if (i < n) {
		return i-m;//
	}
	else{
		return -1;
	}
}