算法复杂度
时间复杂度: 常对幂指阶
时间复杂度
时间复杂度指输入数据大小为 N 时,算法运行所需花费的时间。统计的是算法的「计算操作数量」,而不是「运行的绝对时间」。
时间复杂度具有「最差」、「平均」、「最佳」三种情况,分别使用 O ,Θ ,Ω 三种符号表
常见种类: O(1)<O(logN)<O(N)<O(N*logN)<O(N2)<O(2n)<O(N!)
N2 :如冒泡排序
指数阶常出现于递归
阶乘阶对应数学上常见的 “全排列”
对数阶与指数阶相反,指数阶为 “每轮分裂出两倍的情况” ,而对数阶是 “每轮排除一半的情况” 。对数阶常出现于「二分法」、「分治」等算法中,体现着 “一分为二” 或 “一分为多” 的算法思想。
线性对数阶(N*logN)常出现于排序算法,例如「快速排序」、「归并排序」、「堆排序」等
空间复杂度
通常情况下,空间复杂度指在输入数据大小为 N 时,算法运行所使用的「暂存空间」+「输出空间」的总体大小。
而根据不同来源,算法使用的内存空间分为三类:
指令空间:编译后,程序指令所使用的内存空间。
数据空间:算法中的各项变量使用的空间,包括:声明的常量、变量、动态数组、动态对象等使用的内存空间。
栈帧空间:程序调用函数是基于栈实现的,函数在调用期间,占用常量大小的栈帧空间,直至返回后释放。栈帧空间的累计常出现于递归调用
常见种类:O(1)<O(logN)<O(N)<O(N2)<O(2N)
acwing模板
基础算法
排序
快速排序
快速排序是不稳定的
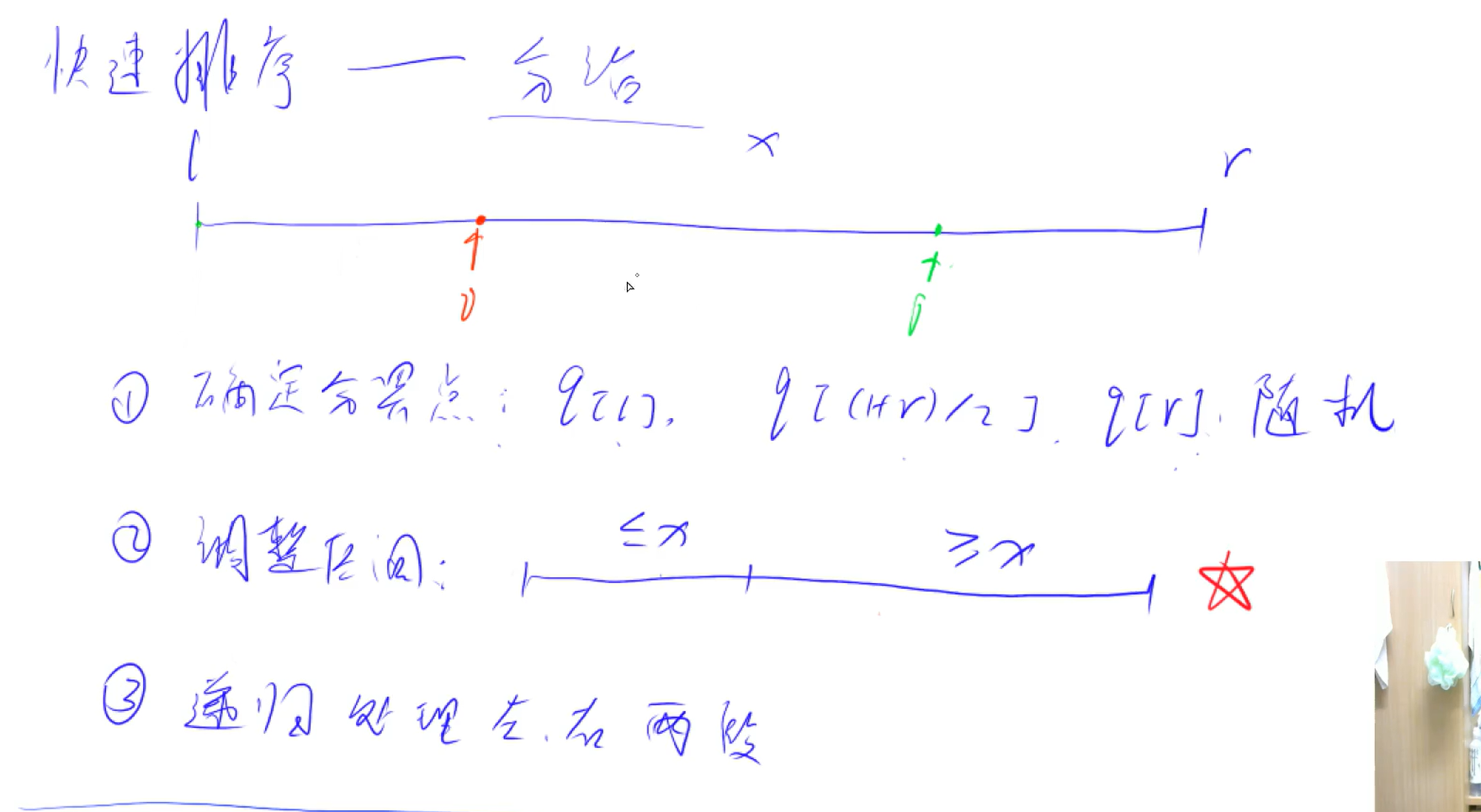
关键:在于如何划分为两个序列
时间复杂度:O(n logn)
const int N = 1e6 + 10;
int q[N];
int n;
void quick_sort(int q[], int l, int r){//l是左边界,r是右边界
if(l >= r) return;//当l和r相遇时,交换l和r位置
int x = q[l + r >> 1];//定义一个中间值,用于比较,把q[]分成大于和小于两部分,更新了数据,不能用最左边和最右边了
int i = l-1, j = r+1;
while(i < j){
do i++; while(q[i] < x);
do j--; while(q[j] > x);
if( i < j ) swap(q[i],q[j]);//如果两个数满足在q[]的分别在另一边,交换位置
}
quick_sort(q,l, j);
quick_sort(q, j + 1, r);//两侧迭代,直到有序
}
归并排序
归并排序是稳定的
关键:在于如何合并连个有序序列,双路归并,合二为一
时间复杂度:O(n logn)

const int N = 1e6 + 10;
int n;
int a[N],tmp[N];
void merge_sort(int q[], int l, int r){
if(l >= r) return;
//确定分界点
int mid = l + r >>1;
//递归分成左右两段
merge_sort(q,l,mid);
merge_sort(q, mid+1, r);
int k = 0, i = l, j = mid + 1;
while(i <= mid&&j <= r){//判断是否结束遍历
if(q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
}
while(i <= mid) tmp[k++] = q[i++];
while(j <= r) tmp[k++] = q[j++];
//把tmp临时数组再赋值回去
for(int i = l, k = 0; i <= r; i++){
q[i] = tmp[k++];
}
}
快速排序和归并排序区别
1.速排序是原地排序,原地排序指的是空间复杂度为O(1);
2.归并排序不是原地排序,因为两个有序数组的合并需要额外的空间协助才能合并;
3.快速排序是不稳定的,时间复杂度在O(nlogn)~O(n2)之间 。归并排序是稳定的,时间复杂度是O(nlogn)。
4.快速排序是二叉树模型
5.归并排序是到二叉树模型
二分
有序元素(有某种性质)+查找 == 二分
整数二分
二分的本质不是单调性,是二段性,将区间一分为二,一半满足,一半不满足

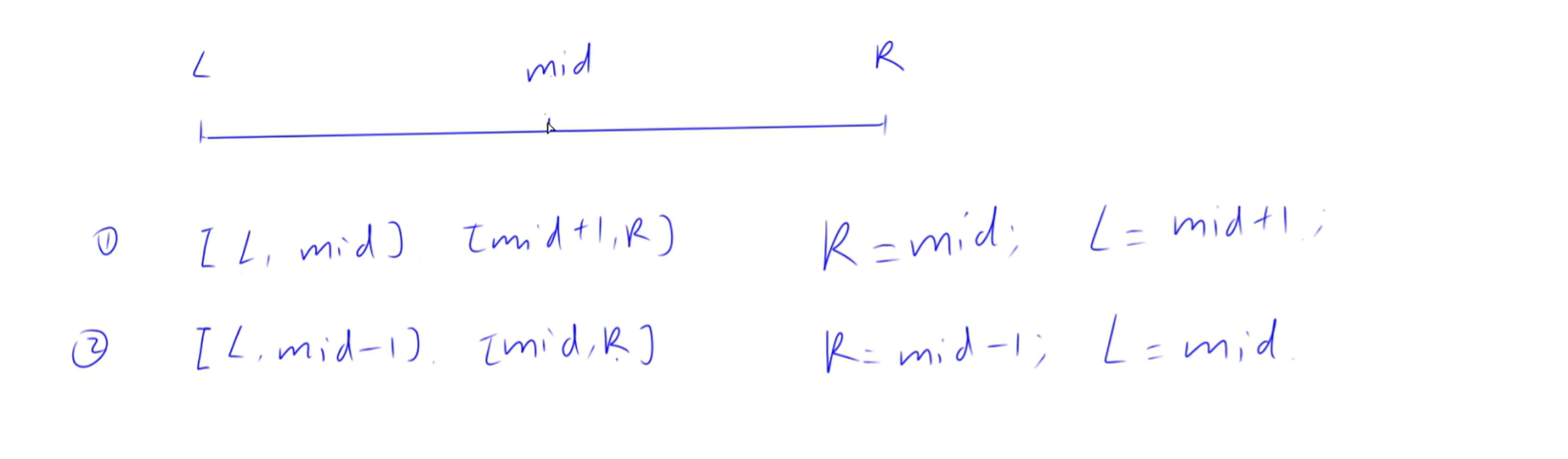
找分界点位置,分为两种,
第一种,找红色边界点,l = mid,而且mid = l+r+1 >>1
第二种,找绿色边界点,r = mid,mid = l + r >> 1
int l = 0, r = n-1;
bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
有点乱,看到还有一种方法,试试看
模板
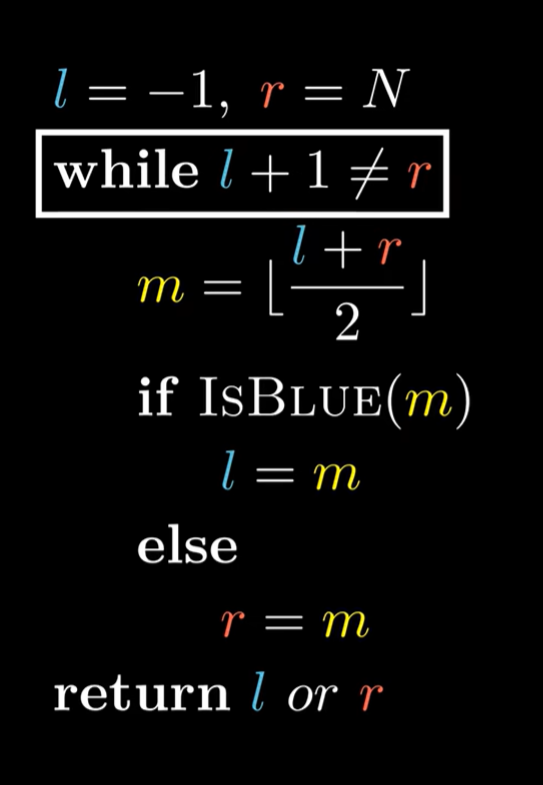

const int N = 1e6 + 10;
int q[N];
bool check(int x){
//要求数据的补集
if() return true;
return false;
}
int l = -1, r = n ;
while(l + 1 != r){
int mid = l + r >> 1;
if(check(q[mid])){
l = m;
}
else r = m;
}
这个方法,更容易出错,返回l,r也有区别
浮点数二分
这个比较简单,一般用于开方
int l = -100, r = 100;
while(r - l > 1e-6){//根据题目要求,一般情况下比题目保留位数大两位
int mid = ( l + r ) / 2;
if(mid * mid >= x) r = m;//x为带求开方数
else l = m;
}
高精度
高精度一般考四种
存储方式用数组,倒序存,从个位存到高位
a + b 位数一般106

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
//加法
vector<int>add(vector<int>&A, vector<int> &B){//这里用引用避免了复制,节省了时间
vector<int>c;
int t = 0;//t表示进位
for(int i = 0; i < A.size()||i < B.size(); i++){
if(i < A.size()) t += A[i];
if(i < B.size()) t += B[i];
c.push_back(t%10);
t /= 10;
}
if(t != 0)
c.push_back(t);
return c;
}
int main()
{
string a,b;
vector<int>A,B;
cin>>a>>b;
//倒序存放到数组的过程
for(int i = a.size() - 1; i >= 0; i --) A.push_back(a[i] - '0');
for(int i = b.size() - 1; i >= 0; i --) B.push_back(b[i] - '0');
//加法
auto c = add(A,B);
//倒序取出
for(int i = c.size() - 1 ; i >= 0; i --){
printf("%d",c[i]);
}
return 0;
}
a - b 位数一般106
t表示借位
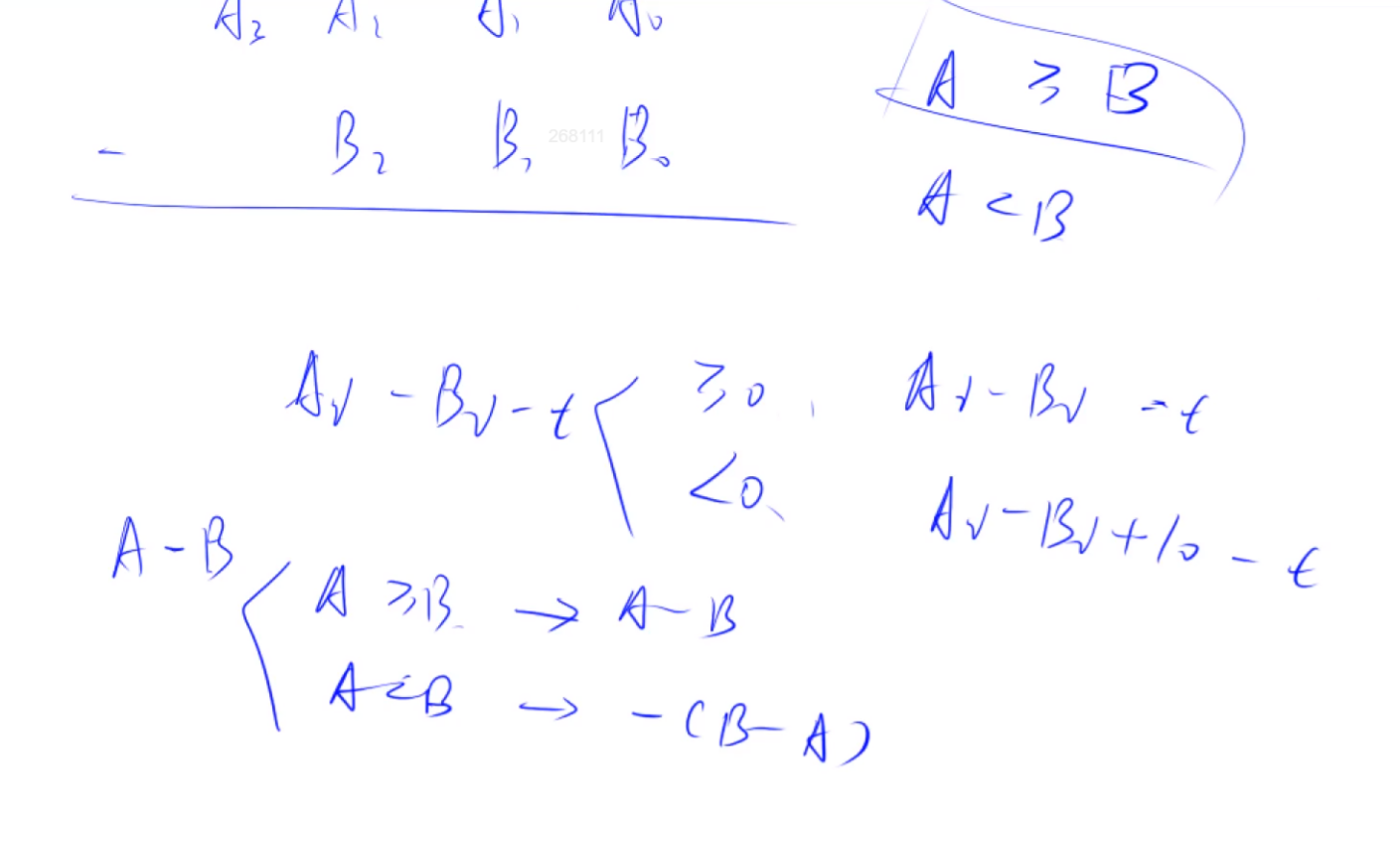
#include <iostream>
#include <string>
#include <vector>
using namespace std;
const int N = 1e5 + 10;
//判断a >= b
bool cmp(vector<int> &a, vector<int> &b){
if(a.size() != b.size()) return a.size() > b.size();
for(int i = a.size() -1; i >= 0; i--){
//找到一位不同数字
if(a[i] != b[i])
return a[i] > b[i];
}
return true;
}
//c = a - b
vector<int> sub(vector<int> &a, vector<int> &b){
vector<int> c;
for(int i = 0, t = 0; i < a.size(); i++){
//t表示借位
t = a[i] - t;
//判断b还有数字
if(i < b.size()) t -= b[i];
//原本要分为两种情况,t > 0 和 t < 0, 这样处理直接不需要分
c.push_back((t + 10) % 10);
if(t < 0) t = 1;//表明要借位
else t = 0;
}
while (c.size() > 1 && c.back() == 0) c.pop_back();
return c;
}
int main()
{
string n,m;
cin>>n>>m;
vector<int> a, b;
for(int i = n.size() - 1; i >= 0; i--) a.push_back(n[i] - '0');
for(int j = m.size() - 1; j >= 0; j--) b.push_back(m[j] - '0');
vector<int>c; // 存结果
//如果a>b
if(cmp(a,b)) {
c = sub(a,b);
}
else c = sub(b, a), cout<<"-";
//输出
for(int i = c.size() - 1; i >= 0; i--){
cout<<c[i];
}
cout<<endl;
return 0;
}
a * b 大整数乘以一个小整数len(a) ≤ 106 且b ≤ 106
把小的数字当做一个整体
#include <iostream>
#include <vector>
using namespace std;
// c = a * b
vector<int> mul(vector<int> &a, int b)
{
vector<int> c;
int t = 0; // 进位
for (int i = 0; i < a.size() || t; i++) // 当i没有处理完,或者t不为0
{
if (i < a.size())
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while(c.size() > 1&&c.back() == 0) c.pop_back();
return c;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector<int> c;
for (int i = a.size() - 1; i >= 0; i--)
{
c.push_back(a[i] - '0');
}
auto s = mul(c, b);
for (int i = s.size() - 1; i >= 0; i--)
{
cout << s[i];
}
return 0;
}
a / b 求商和余数 大整数除以一个小整数len(a) ≤ 106 且b ≤ 106
注意倒着存,正着算

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// a/b,商是c,余数是r
vector<int> div(vector<int> &a, int b, int &r)
{
vector<int> c;
r = 0;
// 注意这里是正着的算的,但是a是倒着存的,所以如下
for (int i = a.size() - 1; i >= 0; i--)
{
r = r * 10 + a[i];
c.push_back(r / b);
r %= b;
}
//翻转过来,正着除,倒着存,翻转过来
reverse(c.begin(), c.end());
// 去掉前导0
while (c.size() > 1 && c.back() == 0)
c.pop_back();
return c;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector<int> c;
for (int i = a.size() - 1; i >= 0; i--)
{
c.push_back(a[i] - '0');
}
int r;
auto s = div(c, b, r);
for (int i = s.size() - 1; i >= 0; i--)
{
cout << s[i];
}
cout << endl<< r;
return 0;
}
前缀和
一维前缀和
前缀和一定要下标从1开始,快速求出数组中一段数的和,sum[0] = 0;
const int N = 100001;
int sum[N],a[N];
for(int i = 1; i <= n; i++){
sum[i] = sum[i-1] + a[i];
}
int ans = sum[r] - sum[l-1];
询问是O(1),预处理过程中是O(n)
对于二维矩阵的前缀和
const int N = 1010;
int sum[N][N],a[N][N];
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
cin>>a[i][j];
sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + a[i][j];
}
}
//(x2,y2) - (x1,y1);
int ans = sum[x2][y2] - sum[x2][y1-1] - sum[x1-1][y2] + sum[x1-1][y1-1];
差分
一维差分
构造一个b数组使得a是b的前n项和
#include<iostream>
using namespace std;
const int N = 100010;
int n,m;
int A[N],B[N];//b数组是a数组的差分,a数组是b数组的前缀和
void insert(int l, int r, int c){
B[l] += c;
B[r+1] -= c;
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n;i++){//注意从一开始
scanf("%d",&A[i]);
}
for(int i = 1; i <= n; i++) insert(i,i, A[i]);
while(m--){
int l,r,c;
scanf("%d%d%d",&l,&r,&c);
insert(l,r,c);
}
for(int i = 1; i<= n; i++){
B[i] += B[i-1];
printf("%d ",B[i]);
}
return 0;
}
二维差分

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int A[N][N],B[N][N];
void insert(int x1, int y1, int x2, int y2, int c){
B[x1][y1] += c;
B[x2 + 1][y1] -= c;
B[x1][y2+1] -= c;
B[x2 + 1][ y2 + 1] += c;
}
int main(){
int n,m,q;
cin>>n>>m>>q;
for (int i = 1; i <= n; i ++ ){
for (int j = 1; j <= m; j ++ ){
cin>>A[i][j];
insert(i,j,i,j,A[i][j]);
}
}
while(q--){
int x1,y1,x2,y2,c;
cin>>x1>>y1>>x2>>y2>>c;
insert(x1,y1,x2,y2,c);
}
for(int i= 1; i <= n; i++){
for(int j = 1; j <= m; j++){
B[i][j] += B[i][j-1]+ B[i-1][j] - B[i-1][j-1];
printf("%d ",B[i][j]);
}
cout<<endl;
}
}
双指针算法
找到某种单调性
可以把O(n2) 的算法优化成O(n)
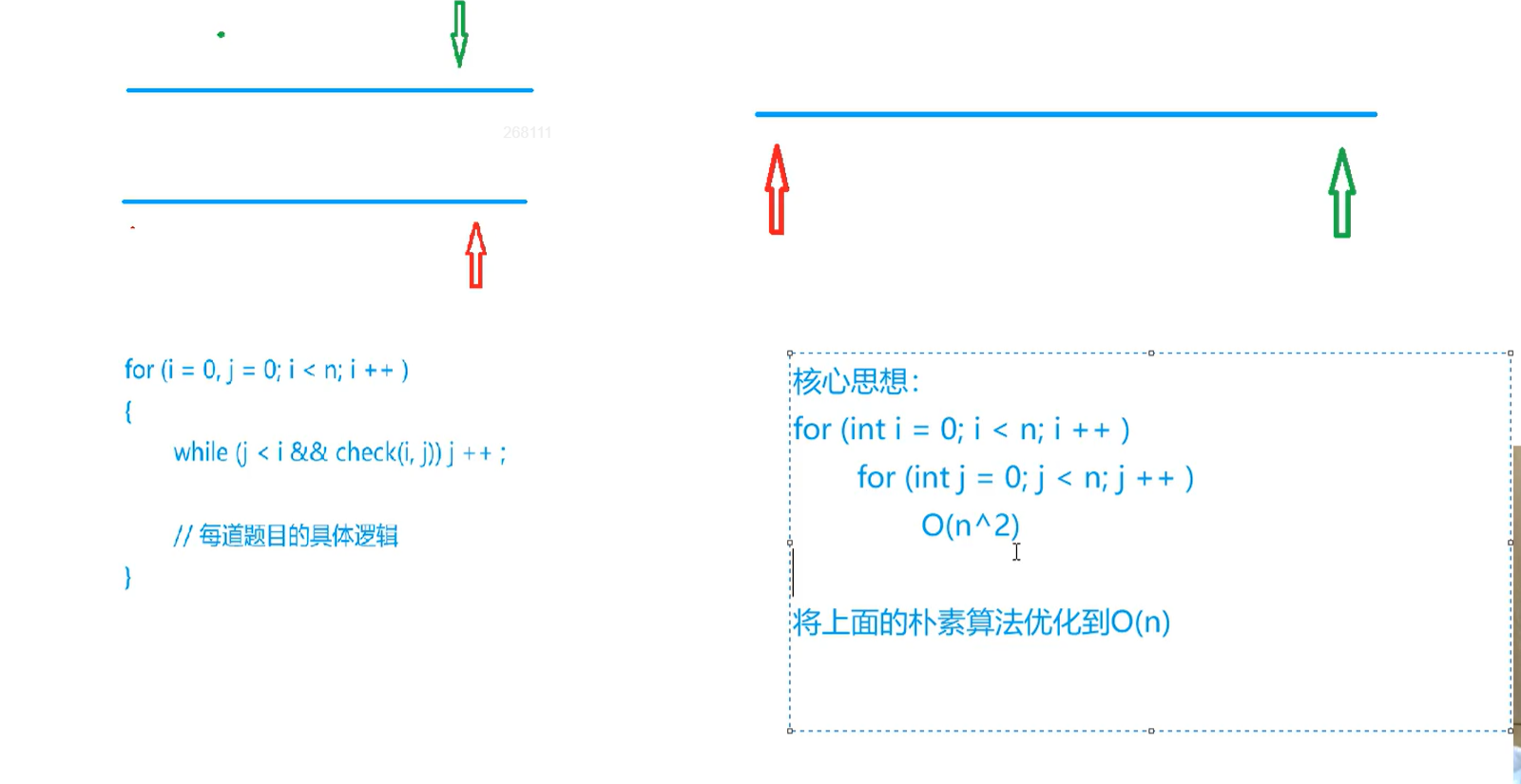
双指针算法将暴力的优化一下
位运算
| 操作符 | 数字a | 数字b | 结果 |
|---|---|---|---|
| & | 0101 | 0001 | 0001 |
| 或 | 0101 | 0001 | 0101 |
| ~ | 0101 | 1010 | |
| ^ | 0101 | 0001 | 0100 |
| >>(右移) | /=2 | ||
| <<(左移) | *=2 |
n的二进制表示中,第k位是几
先把k右移到最后一位 n >> k (n>>1 == n/=2)
在进行与运算 n & 1;
组合起来就是 n >> k & 1;
lowbit(x)是返回x的最后一位1是多少,可以用来统计x中1的个数
实现方式
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int lowbit(int x){
return x & -x;
}
int main(){
int n;
cin>>n;
while(n--){
int x;
cin>>x;
int res = 0;
while(x) {
x -= lowbit(x);//减去x中最后一位1
res++;
}
cout<<res <<' ';
}
return 0;
}
原码:原来的 x
反码:每一位取反 ~x
补码:取反在加一 ~x+1
离散化
这里特指有序、饱序的数字的离散化
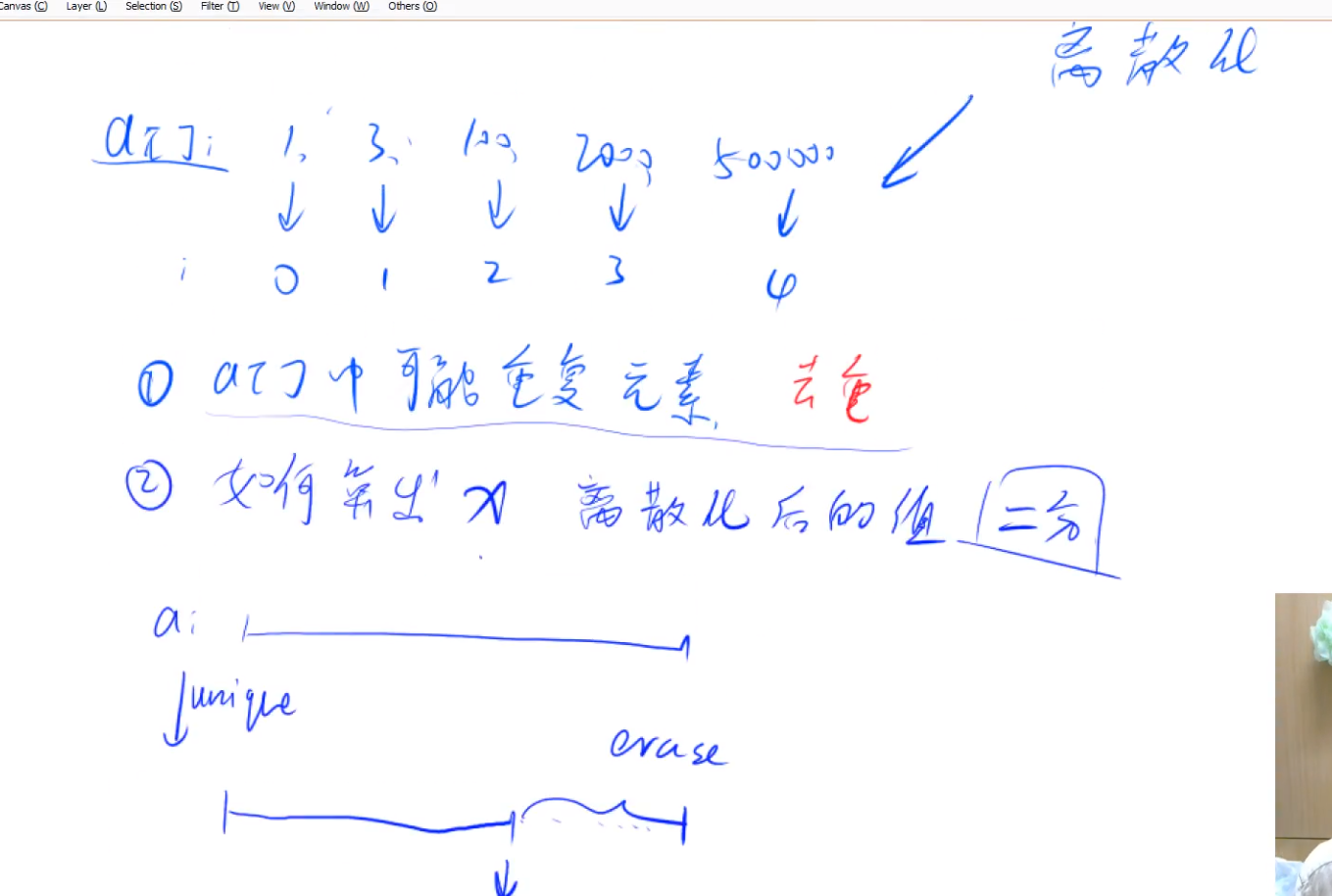
模板
vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 去掉重复元素
// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
int l = 0, r = alls.size() - 1;
while (l < r)
{
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1; // 映射到1, 2, ...n
}
unique实现

//a[j] 中存储的就是不重复元素
vector<int>::iterator unique(vector<int> &a){
int j = 0;
for(int i = 0; i < a.size(); i++){
if(!a || a[i]!=a[i-1]){
a[j++] = a[i];
}
}
return a.begin() + j;
}
这是典例,区间和
#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 300010;
typedef pair<int, int> PII;
vector<int> alls;//存储要离散化的位置
vector<PII> add,query;//插入操作,查询
int a[N],s[N];//a是输入的数,s是前缀和
//求x离散化后的结果,这里用到二分
int find(int x){
int l = 0;
int r = alls.size() - 1;
while(l < r){
int mid = l + r >> 1;
if(alls[mid] >= x) r = mid;//找大于等于x的最小值
else l = mid + 1;
}
return r + 1;//方便进行前缀和
}
int main(){
int n,m;
cin >> n >> m;
for (int i = 0; i < n; i++){
int x,c;
cin>>x>>c;
//在x的位置插入c
add.push_back({x,c});
alls.push_back(x);
}
for (int j = 0; j < m; j++){
int l,r;
cin>>l>>r;
query.push_back({l,r});
alls.push_back(l);
alls.push_back(r);
}
//去重alls
sort (alls.begin(),alls.end());
alls.erase(unique(alls.begin(),alls.end()), alls.end());
//处理插入
for(auto item : add){
int x = find(item.first);
a[x] += item.second;
}
//预处理前缀和
for(int i = 0; i <= alls.size(); i++){
s[i] = s[i-1] + a[i];
}
for(auto item : query){
int l = find(item.first);
int r = find(item.second);
cout<<s[r] - s[l -1]<<endl;
}
return 0;
}
区间合并

按照左端点进行排序
void merge(vector<PII> &segs)
{
vector<PII> res;
sort(segs.begin(), segs.end());
int st = -2e9, ed = -2e9;
for (auto seg : segs)
//没有任何关系
if (ed < seg.first)
{
if (st != -2e9) res.push_back({st, ed});
st = seg.first, ed = seg.second;
}
//有关系,更新ed
else ed = max(ed, seg.second);
//把最后一个加入到区间里
if (st != -2e9) res.push_back({st, ed});
segs = res;
}
数据结构
链表与邻接表:树与图的存储
数组模拟单链表
主要是避免反复new结点,造成缓慢
用于存储树和图
//head 表示头指针
//e[i] 表示下标为i的结点的值
//next[i] 表示i的下一个结点
//idx 表示当前指导那个位置
int e[N],next[N],idx,head;
//初始化
void init(){
head = -1;
idx = 0;
}
//插入到头结点
void add_to_head(int x){
e[idx] = x;
next[idx] = head;
head = idx;
idx ++;
}
//把x插入到下标为k的后面
void add(int k, int x){
e[idx] = x;
ne[idx] = ne[k];
ne[k] = idx;
idx++;
}
//单链表删除k结点下一个元素
void remove(int k){
ne[k] = ne[ne[k]];
}
//双向链表
int e[N],l[N],r[N],idx; //l[N]代表左侧,r[N]代表右侧
void init(){
idx = 2;
//两个边界
r[0] = 1;
l[1] = 0;
}
//在k右边插入x
void add(int k, int x){
e[idx] = x;
l[idx] = k;
r[idx] = r[k];
l[r[k]] = idx;
r[k] = idx;
idx++;
}
//删除第k个点
void remove(int k){
l[r[k]] = l[k];
r[l[k]] = r[k];
}
邻接表是多个单列表
详见第三章
栈与队列:单调队列、单调栈
// tt表示栈顶
int stk[N], tt = 0;
// 向栈顶插入一个数
stk[ ++ tt] = x;
// 从栈顶弹出一个数
tt -- ;
// 栈顶的值
stk[tt];
// 判断栈是否为空,如果 tt > 0,则表示不为空
if (tt > 0)
{
}
单调栈
找某个数最左边或者右边距离他最近的大于或者小于他的数
常见模型:找出每个数左边离它最近的比它大/小的数
int tt = 0;
for (int i = 1; i <= n; i ++ )
{
while (tt && check(stk[tt], i)) tt -- ;
stk[ ++ tt] = i;
}
时间复杂度O(n)
普通队列
// hh 表示队头,tt表示队尾
int q[N], hh = 0, tt = -1;
// 向队尾插入一个数
q[ ++ tt] = x;
// 从队头弹出一个数
hh ++ ;
// 队头的值
q[hh];
// 判断队列是否为空,如果 hh <= tt,则表示不为空
if (hh <= tt)
{
}
循环队列
// hh 表示队头,tt表示队尾的后一个位置
int q[N], hh = 0, tt = 0;
// 向队尾插入一个数
q[tt ++ ] = x;
if (tt == N) tt = 0;
// 从队头弹出一个数
hh ++ ;
if (hh == N) hh = 0;
// 队头的值
q[hh];
// 判断队列是否为空,如果hh != tt,则表示不为空
if (hh != tt)
{
}
单调队列,滑动窗口
//常见模型:找出滑动窗口中的最大值/最小值
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
while (hh <= tt && check_out(q[hh])) hh ++ ; // 判断队头是否滑出窗口
while (hh <= tt && check(q[tt], i)) tt -- ;
q[ ++ tt] = i;
}
原理差不多,等二刷
#include<iostream>
using namespace std;
const int N = 1000001;
int a[N], q[N];//q[N]存储的是滑动窗口中的下标
int main(){
int n,k;
scanf("%d%d", &n,&k);
for(int i = 0; i < n; i++){
scanf("%d",&a[i]);
}
int hh = 0, tt = -1;
for(int i = 0; i < n; i++){
//判断队头元素是否已经滑出窗口
if (hh <= tt && q[hh] < i - k + 1) hh++;
while(hh <= tt && a[q[tt]] >= a[i]) tt--;
q[++tt] = i;
if(i >= k -1) printf("%d ",a[q[hh]]);
}
puts("");
hh = 0, tt = -1;
for(int i = 0; i < n; i++){
if(hh <= tt && q[hh] < i - k + 1) hh++;
while(hh <= tt && a[q[tt]] <= a[i]) tt--;
q[++tt] = i;
if(i >= k - 1) printf("%d ", a[q[hh]]);
}
puts("");
return 0;
}
kmp
// s[]是长文本,p[]是模式串,n是s的长度,m是p的长度
求模式串的Next数组:
for (int i = 2, j = 0; i <= m; i ++ )
{
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j ++ ;
ne[i] = j;
}
// 匹配
for (int i = 1, j = 0; i <= n; i ++ )
{
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j ++ ;
if (j == m)
{
j = ne[j];
// 匹配成功后的逻辑
}
}
现在还不太懂代码,但是原理懂了
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010, M = 1000010;
int n,m;
char p[N], s[M];
int nex[N];
int main(){
cin>>n>>p + 1>>m >> s+1;
for(int i = 2, j = 0; i <= n; i++){
while(j && p[i] != p[j + 1]) j = nex[j];
if(p[i] == p[j + 1]) j++;
nex[i] = j;
}
for(int i = 1, j = 0; i <= m; i++){
while(j && s[i] != p[j + 1]) j = nex[j];
if(s[i] == p[j + 1]) j++;
if(j == n){
printf("%d ", i- n);
j = nex[j];
}
}
return 0;
}
Trie
高效的存储和查找字符串集合的数据结构
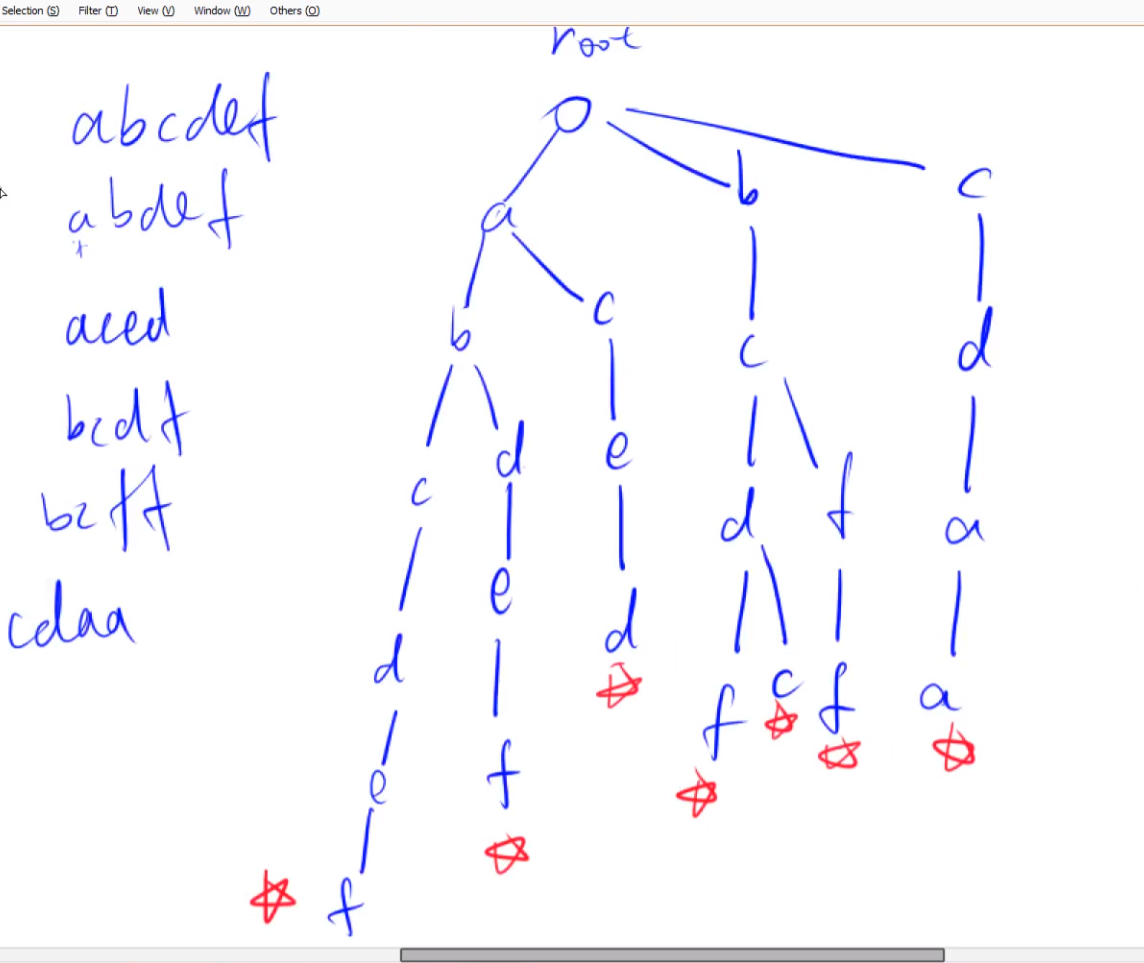
将所有字符串集合的结尾进行标记
int son[N][26], cnt[N], idx;
// 0号点既是根节点,又是空节点
// son[][]存储树中每个节点的子节点
// cnt[]存储以每个节点结尾的单词数量
// idx 存储当前用到那个下标
// 插入一个字符串
void insert(char *str)
{
int p = 0;//从根节点开始遍历
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';//将a-z映射成0-25
if (!son[p][u]) son[p][u] = ++ idx;//如果不存在,就创建出来
p = son[p][u];//结束时对应的结尾位置为p
}
cnt[p] ++ ;
}
// 查询字符串出现的次数
int query(char *str)
{
int p = 0;
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';
if (!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
并查集
两个操作:(近乎O(1))
1.将两个集合合并
2.询问两个元素是否在一个集合中
3.用树的形式维护一个集合,根节点是他的代表元素,根节点的编号就是当前集合的编号,每个节点存储他的父节点,p[x]表示x的父节点
4.判断树根p[x] = x
5.如何求x的集合编号:while(p[x] != x) x = p[x]
6.如何合并两个集合:将一个集合当成另外一个集合的子节点p[x]是x的集合编号,p[y]是y的集合编号,p[x] = y
7.优化:
路径压缩一旦找到根节点,就将该路径上的所有点都指向根节点,基本就可以看成O(1)
按秩合并:先留下,后面在补
(1)朴素并查集:
int p[N]; //存储每个点的祖宗节点
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ ) p[i] = i;
// 合并a和b所在的两个集合:
p[find(a)] = find(b);
// 查找是否在同一个集合
find(a) == find(b);
(2)维护size的并查集:
int p[N], size[N];
//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义,表示祖宗节点所在集合中的点的数量
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
size[i] = 1;
}
// 合并a和b所在的两个集合:这个有顺序,不能错
size[find(b)] += size[find(a)];
p[find(a)] = find(b);
(3)维护到祖宗节点距离的并查集:
int p[N], d[N];
//p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x)
{
int u = find(p[x]);
d[x] += d[p[x]];
p[x] = u;
}
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
d[i] = 0;
}
// 合并a和b所在的两个集合:
p[find(a)] = find(b);
d[find(a)] = distance; // 根据具体问题,初始化find(a)的偏移量
堆
堆是维护一个数据集合,是用一维数组实现的完全二叉树(常常用来构建优先队列,支持堆排序,快速找出一个集合中的最小值或者最大值)
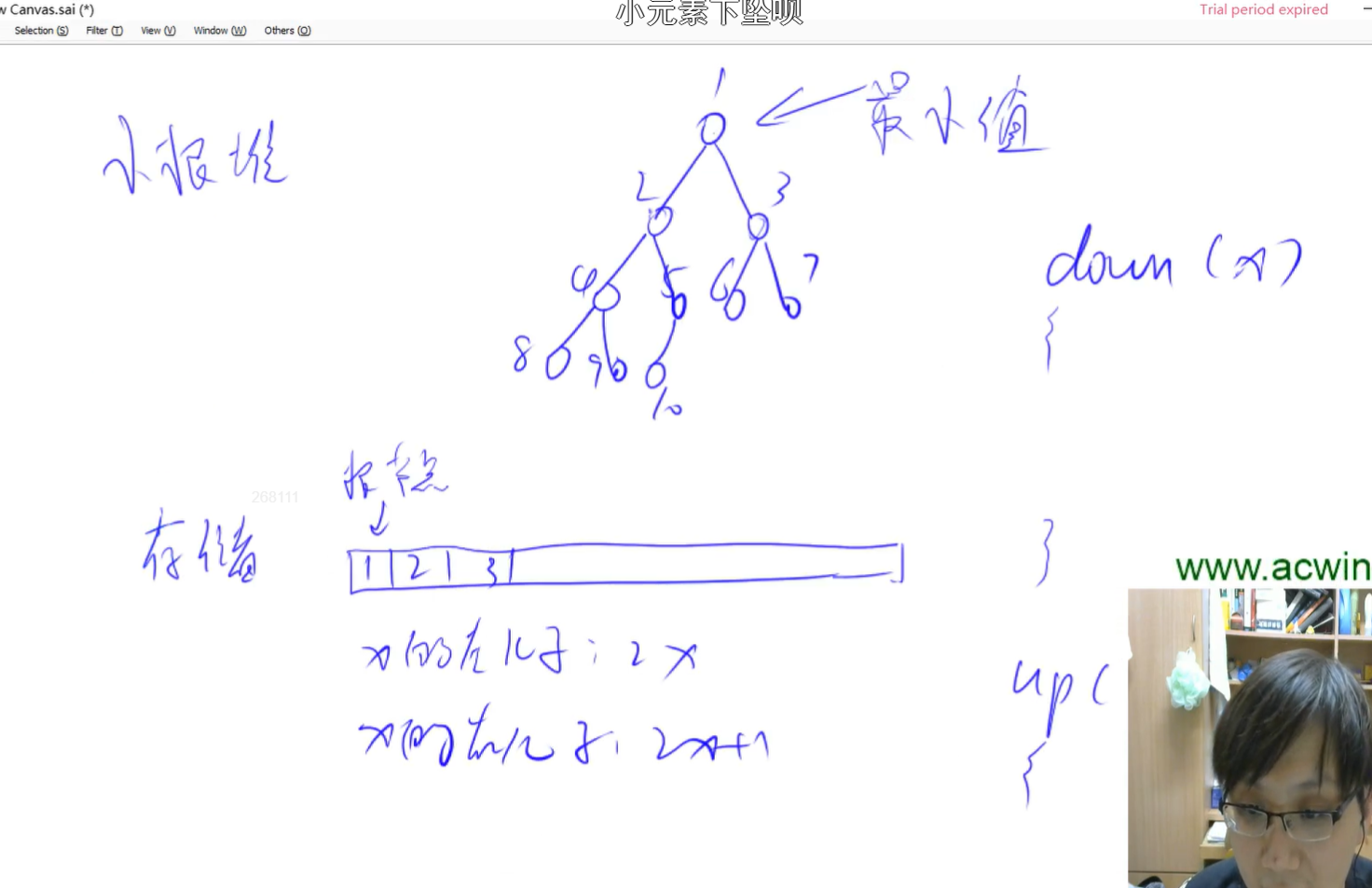
一维数组存贮
x的左儿子是2x
x的右儿子是2x+1
堆排序
这些操作都可以用down(){}和up(){}操作表示
down和up操作是O(logn),求最小值是O(1),插入和删除都时O(logn)
将创建堆得操作从O(nlogn) 下降到 O(n),先插入n/2接下来的都down
Hash表
搜索和图论
DFS与BFS
DFS
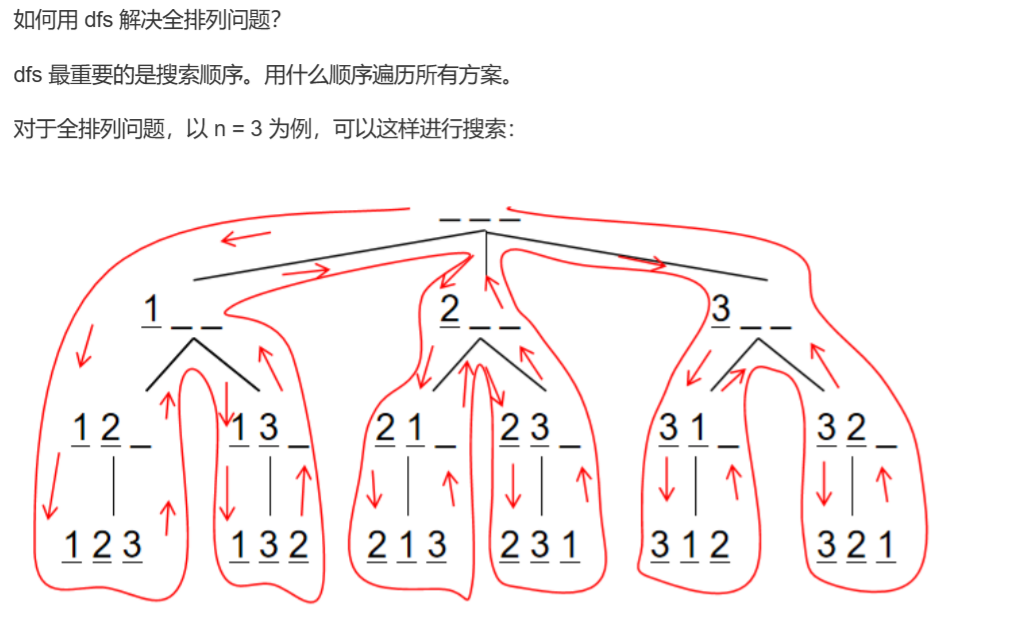
| 数据结构 | 空间 | 特点 | ||
|---|---|---|---|---|
| DFS | stack | O(h) | 不具有最短性 | 最重要的顺序 |
| BFS | queue | O(2n) | 最短路 | |
| 剪枝: | ||||
| 最优性剪枝:不是最优解,剪枝 | ||||
| 可行性剪枝:不可行时候剪枝 |
BFS

/*
做这种题目的步骤(最短路问题)
1.创建两个存储,一个存储值,一个存储距离
2.然后首先将第一个点的位置存储的距离提前标注出来
3.然后弄两个方向变量用于上下左右前进int[] dx = {-1,0,1,0}, dy = {0,1,0,-1};
4.然后如果四个方向上的点没有超过边界,在结合实际情况有没有用过的点,判断能不能够进行前进,如果可以就进行前进存储其内容g跟距离d+1
5.最后返回想要的最短值d;
*/
树与图的遍历:拓扑排序
树是无环联通的特殊的图
图:无向图,有向图
最短路
最小生成树
二分图:染色法、匈牙利算法
数学知识
质数
线性筛素数
const int N = 200000;
int primes[N];
int cnt = 0;
int heshu[N];
void get_primes(int n){
for(int i = 2; i < n; i++){
if(!heshu[i]) primes[cnt++] = i;
for(int j = 0; primes[j] * i <= n; j++){
heshu[primes[j] * i] = true;
if(i % primes[j] == 0) break;
}
}
}
1 ≤ n ≤ 106
时间复杂度O(n)
约数
int gcd(int a, int b)
{
return b ? gcd(b,a%b):a;
}
正常
int gcd(int a, int b){
if(a%b == 0) return b;
else return gcd(b,a%b);
}
欧拉函数
快速幂
快速幂迭代版
求ab mod p
typedef long long LL;
int quickmi(int a, int b, int p){//
int res = 1 %p;
while(b){//对b进行二进制化,从低位到高位
if(b & 1) res = (LL) res * a%p;
//更新a,a依次为a^{2^0},a^{2^1},a^{2^2},....,a^{2^logb}
a = (LL)a * a%p;
//b二进制右移一位
b >>= 1;
}
return res;
}
b&1就是判断b的二进制表示中第0位上的数是否为1,若为1,b&1=true,反之b&1=false
b&1也可以用来判断奇数和偶数,b&1=true时为奇数,反之b&1=false时为偶数
判断二进制第k位的数字为1:n>>k&1 == true;
扩展欧几里得算法
中国剩余定理
高斯消元
组合计数
Cbn = Cbn-1 + Cb-1n-1
const int N = 2001, MOD = 1e9+7;
typedef long long LL;
int C[N][N];
void init(int n){
for(int i = 0; i <= n; i++)
{
for(int j = 0; j <= i; j++){
if(j == 0){C[i][j] = 1;}
else C[i][j] = ((LL)C[i-1][j] + C[i-1][j-1])%MOD;
}
}
}
O(n2)
容斥原理

从n个数中选择任意多个数的方案数,共有2n项,时间复杂度2n


for (int i = 1; i < 1 << m; i ++ )
// i<1<<m 组合数 2^m-1
{
//t表示所有质数的乘积,cnt表示i里面有几个一
int t = 1, s = 0;
for (int j = 0; j < m; j ++ )//遍历二进制的每一位
if (i >> j & 1)//判断二进制第j位是否存在
{
if ((LL)t * p[j] > n)
{
t = -1;
break;
}
t *= p[j];
s ++ ;
}
if (t != -1)
{
if (s % 2) res += n / t;
else res -= n / t;
}
}







 浙公网安备 33010602011771号
浙公网安备 33010602011771号