算法实验课-1:斐波那契数列
算法实验课-1:斐波那契数列
1.定义
斐波纳契数列(Fibonacci sequence)以递归的方法定义：F(0)=0，F(1)=1, F(n)=F(n-1)+F(n-2)（n>=2，n∈N*）
2.求斐波那契数列的算法
2.1递归算法
根据定义实现的算法, 简单易实现
int Fib_Recursive(int n)
{
if(n == 0)
return 0;
else if(n == 1)
return 1;
else if(n == 2)
return 1;
else
return Fib_Recursive(n-1)+Fib_Recursive(n-2);
}
当要求的第n位稍大时, 该算法计算量急剧增大, 用递归方法计算的时间复杂度是以n的指数的方式递增的, 时间复杂度为O(2^n).
2.2迭代算法
定义一个数组 Arr[3] = { 0, 1, 1 } , 当求n = 0 , 1 , 2 时,直接从数组中返回Arr[n].
在n >= 3时,对数组中的数据进行迭代循环来计算第n个斐波那契数列. 例如, 在求第3个斐波那契数时:
Arr[0] <- Arr[1]; // Arr[0] = 1
Arr[1] <- Arr[2]; // Arr[1] = 1
Arr[2] <- Arr[0] + Arr[1];
// Arr[2] = 2, 此时Arr[2]就是第三个斐波那契数
// 如果要求第4个, 就循环这种步骤两次
代码如下:
int Fib_Iteration(int n)
{
int FibArray[3] = {0,1,1};
if(n < 3)
return FibArray[n];
else
{
//从i= 3开始循环
for(int i = 3; i <= n; ++i)
{
FibArray[0] = FibArray[1];
FibArray[1] = FibArray[2];
FibArray[2] = FibArray[0] + FibArray[1];
}
return FibArray[2];
}
}
单层循环，时间复杂度为O(n)
2.3通项公式法
斐波那契数列的通项公式如下:
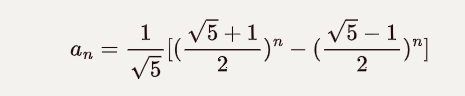
由于这一项
\[(\frac{\sqrt{5}-1}{2})^n
\]
是 0 到 1 之间的小数, 当 n 趋向于无穷大时, 该项趋向于无穷小. 根据证明, 这一项对最终结果的影响, 相当于将第一项的值向最近的整数取整, 所以对于每一个非负整数 n, 有:
\[F(n) = \frac{1}{\sqrt{5}}(\frac{\sqrt{5}+1}{2})^n \quad 向最近的整数取整
\]
double Fib_Formula(int n)
{
double phi = (1 + sqrt(5))/2;
double Fib_n = pow(phi,n) / sqrt(5);
Fib_n = floor(Fib_n + 0.5);
return Fib_n;
}
//由于各个函数返回值是double型,所以最后取整会有小数部分的0
在我的机器上如果返回float类型的值,由于精度的差异,最后一个准确的值是第31个数.
2.4矩阵乘方计算
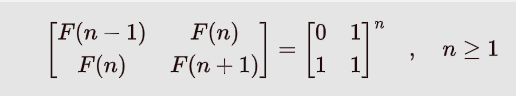
这个算法基于上述公式 , 每次计算只需要对整数进行操作 , 是一个计算斐波那契数列的高效方法.
当以上公式中的 n = 1 时 , 可以在矩阵中找到 F(0) , F(1) , F(2)的值
2.4.1迭代计算矩阵乘方
/* 矩阵乘方 一 */
unsigned int Fib_Matrix(int n)
{
//用二维数保存矩阵初始状态
unsigned int FibMatrix[2][2] = {{0,1},{1,1}};
if(n == 0)
return FibMatrix[0][0];
else if(n == 1)
return FibMatrix[0][1];
else
{
//数组arr保存每次进行矩阵相乘后的结果
unsigned int arr[2][2];
//循环计算矩阵乘方
for(int i = 2; i <= n; ++i)
{
arr[0][0] = FibMatrix[0][0] * 0 + FibMatrix[0][1] * 1;
arr[0][1] = FibMatrix[0][0] * 1 + FibMatrix[0][1] * 1;
arr[1][0] = FibMatrix[1][0] * 0 + FibMatrix[1][1] * 1;
arr[1][1] = FibMatrix[1][0] * 1 + FibMatrix[1 ][1] * 1;
//将arr中的结果赋给FibMatrix, 用于下一次矩阵乘法
for(int j = 0; j < 2; ++j)
{
for(int k = 0; k < 2; ++k)
FibMatrix[j][k] = arr[j][k];
}
}
return FibMatrix[0][1];
}
}
/* 此种方式在计算矩阵的n次幂 (n >= 2) 时,要进行 n-1 次循环运算
所以采用分治法计算矩阵的乘方
*/
2.4.2分治法计算矩阵乘方
要计算 a^n , 有以下两种情况
-
n 为偶数时 , 有:
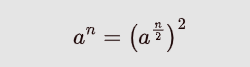
再继续判断 n/2 的奇偶性; -
n 为奇数时 , 有:
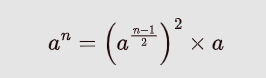
再继续判断(n-1)/2 的奇偶性; -
直到判断到 n/2 或 (n-1)/2 等于1时 , 开始回溯计算矩阵乘方 , 这样求幂运算的复杂度为O(log n)
/* 矩阵乘方 二 */
//这里的递归return的 值 在运算中没有实际作用,
//传入的第一个参数 数组名 相当于传地址调用
//可以将矩阵乘方的结果带回上一层递归
//计算矩阵乘方
unsigned int Matrix_Pow(unsigned int arr[2][2], int n)
{
if(n == 1)
{
arr[0][0] = 0;
arr[0][1] = 1;
arr[1][0] = 1;
arr[1][1] = 1;
return 0;
}
else
{
//偶数情况
if(n % 2 == 0)
{
Matrix_Pow(arr, n/2);
//临时保存矩阵相乘结果
unsigned int temp[2][2];
//这里的计算过程应该再封装一下, 代码就不会那么恶心了,跟baba一样
temp[0][0] = arr[0][0] * arr[0][0] + arr[0][1] * arr[1][0];
temp[0][1] = arr[0][0] * arr[0][1] + arr[0][1] * arr[1][1];
temp[1][0] = arr[1][0] * arr[0][0] + arr[1][1] * arr[1][0];
temp[1][1] = arr[1][0] * arr[0][1] + arr[1][1] * arr[1][1];
//重新赋值给arr数组
for(int j = 0; j < 2; ++j)
{
for(int k = 0; k < 2; ++k)
arr[j][k] = temp[j][k];
}
return 1;
}
else
{
Matrix_Pow(arr, (n-1)/2);
unsigned int temp[2][2];
temp[0][0] = arr[0][0] * arr[0][0] + arr[0][1] * arr[1][0];
temp[0][1] = arr[0][0] * arr[0][1] + arr[0][1] * arr[1][1];
temp[1][0] = arr[1][0] * arr[0][0] + arr[1][1] * arr[1][0];
temp[1][1] = arr[1][0] * arr[0][1] + arr[1][1] * arr[1][1];
//奇数情况矩阵相乘后,还要再次与初始矩阵相乘
arr[0][0] = temp[0][0] * 0 + temp[0][1] * 1;
arr[0][1] = temp[0][0] * 1 + temp[0][1] * 1;
arr[1][0] = temp[1][0] * 0 + temp[1][1] * 1;
arr[1][1] = temp[1][0] * 1 + temp[1][1] * 1;
return 2;
}
}
}
//调用分支计算矩阵函数, 得到最终结果
unsigned int Fib_Matrix(int n)
{
//二维数组表示矩阵初始状态
unsigned int FibMatrix[2][2] = {{0,1},{1,1}};
if(n == 0)
return FibMatrix[0][0];
else if(n == 1)
return FibMatrix[0][1];
else
{
//将数组 arr 作为参数传入计算矩阵乘方的函数
unsigned int arr[2][2];
Matrix_Pow(arr,n);
return arr[0][1];
}
}
3.总结
整体来说这几种方法只要知道定义或者相关公式都还是比较好实现, 还有本次实验课的一些花里胡哨的要求就不记录了,还有就是矩阵那段乘法不封装是真的难看, 不过就这样吧😂
