栈与递归

　　递归的概念

　　栈的一个典型应用是程序设计中的递归过程的设计与实现，用栈来保存调用过程中的参数和返回地址。

递归过程(或函数)就是子程序或函数中直接或间接的调用自己。

　　递归定义实例：

　　1.某人祖先的递归定义：

某人的双亲是他的祖先[基本情况]

某人祖先的双亲同样是某人的祖先[递归步骤]

　　2.阶乘函数

       

　　 3.斐波那契数列

 

 

 　　一般递归分为直接递归和间接递归

 

                     

 

 

 

 

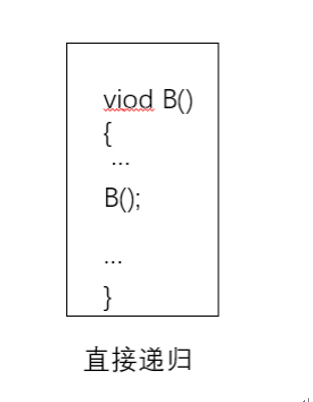
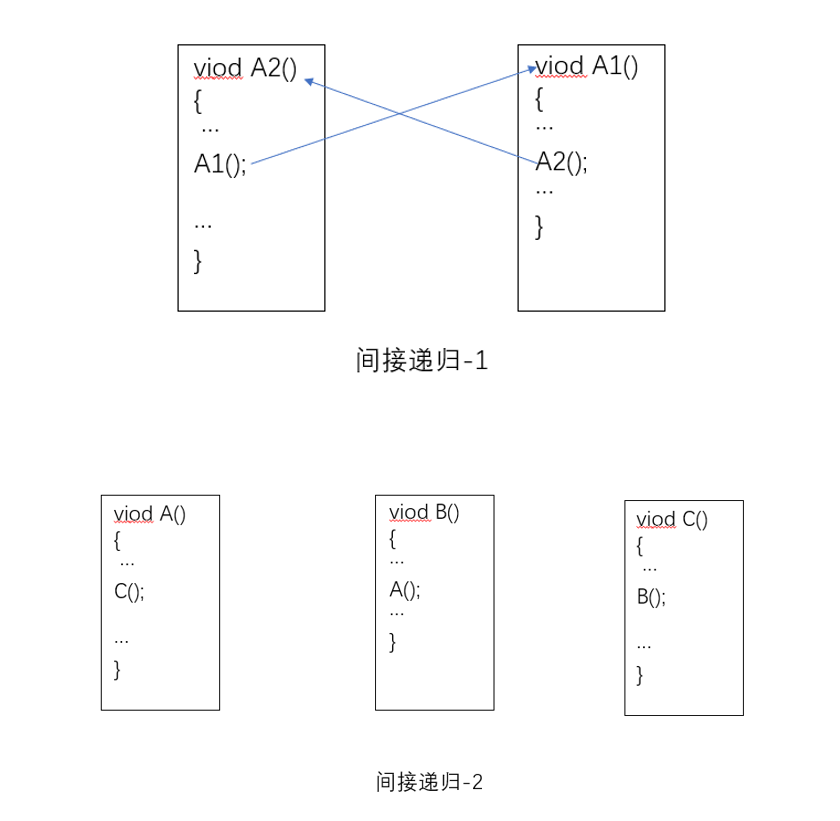
　　4.Ackerman函数

　　当两个连续函数都趋近于无穷时，我们常用洛必达法则来比较它们趋向无穷的快慢。函数的阶越高，

它趋向无穷的速度就越快。定义在正整数域上的函数中，n!趋向于正无穷的速度非常快，所以在算法设计中

如果出现这样的时间复杂度就非常糟糕。log_n趋向无穷的速度则非常慢。

　　 而Ackerman函数可以比n!的增长速度快得多，比log_n的增长速度慢的多。同时，并不是所有的

递归函数都有通项公式，Ackerman函数就是一个例子，它是双向递归函数，有两个自变量(独立)，定义如下:

  

              Ack(0,n)=n+1 , n>=0;

             

              Ack(m,0)=Ack(m-1,1) , m>0;

             

              Ack(m,n)=Ack(Ack(m-1,n),n-1) , n,m>0

#include <stdio.h>

#include <stdlib.h>

int   ack(int  m, int   n)

{

    int    z;

    if (m == 0)

         z = n + 1; //出口

    else if (n == 0)

         z = ack(m - 1, 1);  //形参m降阶

    else

         z = ack(m - 1, ack(m, n - 1)); //对形参m,n降阶

    return z;

}

        

void main() {

     int  m, n;

    scanf("%d%d", &m, &n);

    printf("Ack(%d,%d)=%d\n",m,n, ack(m, n));

 

} 

 

 

　　递归过程的内部实现

　　从递归调用的过程可知，它们刚好符合后进先出的原则。因此，利用栈实现递归过程再合适不过。

下面以求n!为例，介绍它的递归实现过程。

  递归算法为

  

int fact(int N)

{

int result;

if(N == 0)

result = 1;

else

result = fact(n-1)*n  //递归调用自身

return result;

}

 

 　　在递归执行过程中，需要一个栈LS保存递归调用前的参数及递归的返回地址。参数为fact中的现行值，返回地址为递归语句的下一语句入口地址。设第1次调用的返回地址为p1，第2次调用的返回地址为p2, … 如图1所示

 具体实现为

(1)遇递归调用时，将当前参数与返回地址保存在LS中;

(2)遇递归返回语句时，将LS栈顶的参数及返回地址一并弹出，按当前返回地址继续执行

 

 

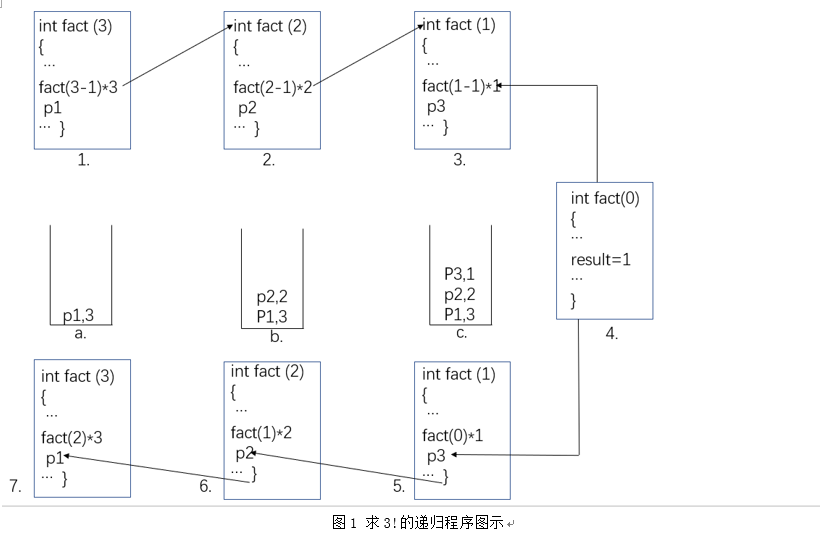
  分析递归程序的运行机制,递归用需要1-7的过程，而非递归只需要4-7过程，可见递归程序的运行效率并不高，

即并不能节约运行时间，相反，由于保存大量的递归调用的参数和返回地址，还要消耗一定的时间，再加上空间上的消耗，

同非递归递归函数相比毫无优势而言。但是尽管递归在时空方面不占优势，但有编程方便，结构清楚，逻辑结构严谨等优势。

递归的致命缺点是时空性能不好，但是我们可以用非递归方法来解决递归问题，从而改善程序的时空性能。

递归消除

       递归的消除有两种：简单递归消除和基于栈的递归消除

　　1.简单递归消除

　　尾递归是指递归调用用语句只有一个, 且处于算法的最后,尾递归是单向递归的特例. n!递归算法是尾递归的一个典型例子.

  对于尾递归,当递归返回时, 返回到上一层递归调用语句的下一语句时已到程序的末尾, 所以不需要栈LS保存返回地址。

　　2.基于栈的递归消除

　　具体方法：将递归算法中的递归调用语句改成压入操作；将递归返回语句改为弹出操作。

sqstack.h：

https://www.cnblogs.com/mwq1024/p/10146943.html

//计算n！不需要保存返回地址 原因上面说了

#include <stdio.h>

#include <stdlib.h>

#include "sqstack.h" //引入顺序栈储存结构及其基本操作

 

int fact(int N) {

    int result = 1;

    SqStack s,*S;

    S = &s;

    StackType *e;

    e = (StackType*)malloc(sizeof(StackType));

    InitStack(S);

    while (N)

    {

         Push(S, N);

         N--;

    }

    while (!EmptyStack(S))

    {

         result *= *(S->top - 1);

         Pop(S, e);

    }

    return result;

   

}

void main()

{

    int n;

    printf("请输入n的阶数:");

    scanf("%d", &n);

    printf("result is %d\n", fact(n));

}

 

    利用栈解决汉诺塔问题

    把三个塔座看成三个栈，入栈和出栈就相当于移动盘子。

汉诺塔算法的非递归实现C++源代码

　　

#include <iostream>

using namespace std;

//圆盘的个数最多为64

const int MAX = 64;

//用来表示每根柱子的信息

struct st{

int s[MAX]; //柱子上的圆盘存储情况

int top; //栈顶，用来最上面的圆盘

char name; //柱子的名字，可以是A，B，C中的一个

 

int Top()//取栈顶元素

{

return s[top];

}

int Pop()//出栈

{

return s[top--];

}

void Push(int x)//入栈

{

s[++top] = x;

}

} ;

long Pow(int x, int y); //计算x^y

void Creat(st ta[], int n); //给结构数组设置初值

void Hannuota(st ta[], long max); //移动汉诺塔的主要函数

int main(void)

{

int n;

cin >> n; //输入圆盘的个数

st ta[3]; //三根柱子的信息用结构数组存储

Creat(ta, n); //给结构数组设置初值

long max = Pow(2, n) - 1;//动的次数应等于2^n - 1

Hannuota(ta, max);//移动汉诺塔的主要函数

system("pause");

return 0;

}

void Creat(st ta[], int n)

{

ta[0].name = 'A';

ta[0].top = n-1;

//把所有的圆盘按从大到小的顺序放在柱子A上

for (int i=0; i<n; i++)

ta[0].s[i] = n - i;

//柱子B，C上开始没有没有圆盘

ta[1].top = ta[2].top = 0;

for (int i=0; i<n; i++)

ta[1].s[i] = ta[2].s[i] = 0;

//若n为偶数，按顺时针方向依次摆放 A B C

if (n%2 == 0)

{

ta[1].name = 'B';

ta[2].name = 'C';

}

else //若n为奇数，按顺时针方向依次摆放 A C B

{

ta[1].name = 'C';

ta[2].name = 'B';

}

}

long Pow(int x, int y)

{

long sum = 1;

for (int i=0; i<y; i++)

sum *= x;

return sum;

}

void Hannuota(st ta[], long max)

{

int k = 0; //累计移动的次数

int i = 0;

int ch;

while (k < max)

{

//按顺时针方向把圆盘1从现在的柱子移动到下一根柱子

ch = ta[i%3].Pop();

ta[(i+1)%3].Push(ch);

cout << ++k << ": " <<

"Move disk " << ch << " from " << ta[i%3].name <<

" to " << ta[(i+1)%3].name << endl;

i++;

//把另外两根柱子上可以移动的圆盘移动到新的柱子上

if (k < max)

{ //把非空柱子上的圆盘移动到空柱子上，当两根柱子都为空时，移动较小的圆盘

if (ta[(i+1)%3].Top() == 0 ||

ta[(i-1)%3].Top() > 0 &&

ta[(i+1)%3].Top() > ta[(i-1)%3].Top())

{

ch = ta[(i-1)%3].Pop();

ta[(i+1)%3].Push(ch);

cout << ++k << ": " << "Move disk "

<< ch << " from " << ta[(i-1)%3].name

<< " to " << ta[(i+1)%3].name << endl;

}

else

{

ch = ta[(i+1)%3].Pop();

ta[(i-1)%3].Push(ch);

cout << ++k << ": " << "Move disk "

<< ch << " from " << ta[(i+1)%3].name

<< " to " << ta[(i-1)%3].name << endl;

            }

        }

    }

}