【线性代数】PCA主成分析与相关概念

降维问题：

首先需要理解的：降维的本质操作时是什么？

 

之前自己理解的只是通过找到一系列新的坐标轴来表示原始数据，但是从来没有细细深究背后的数学原理；

 

例如对于特征空间为二维的坐标点来说，其拥有两个特征，所以在特征空间中采用（x，y）两个参变量进行表示；

 

但是对于我们数据分析来说，如果变化的趋势或者方向明显，往往不需要高维来表示方向；

 

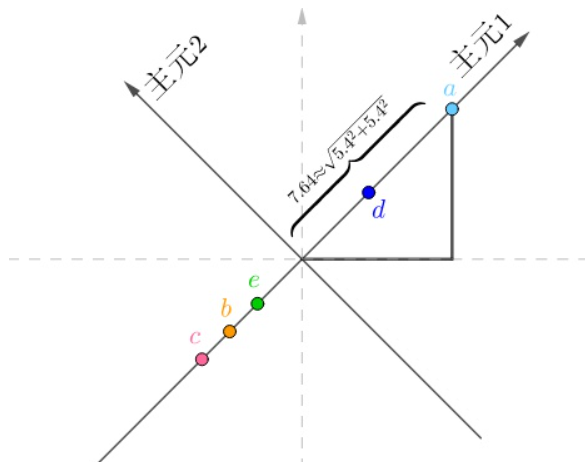
如果我们对上述坐标轴进行新的构建；

 

 

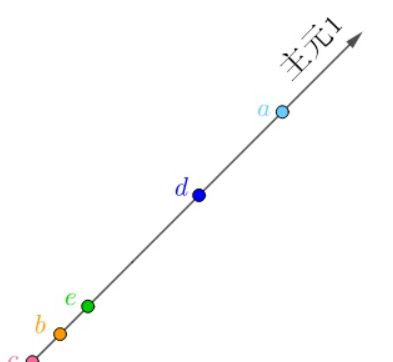
 如上图所示，可以很轻松的看出来，如果采用一个新的主元方向进行一维坐标轴的表示，可以很轻松的减少一个维度的数据，并且也能进行很好的数据预测和分析，这对于计算和模型输入都是很有帮助的；

 

对于空间坐标变换，使用的方法就是采用线性变换，相当于对基向量进行旋转和拉伸，构成新的坐标表示；

因此，这也是为什么线性代数和降维如此息息相关，降维的本质也就是使用一定的方法来寻找出一个新的正交基向量，来表示原本的点，在这过程中也表现为高维特征空间缩减为低维数据空间的过程；

 

对于数学理解来说：

看到别人的博客，对于降维也有不一样的数学描述；

尽管我们对于基向量进行新的寻找和变换，但是唯一不变的是该点到坐标原点的欧氏距离；

所以我们只需要使得某个坐标轴值变为0，在欧氏距离d不变的情况下，增加或者减少其他坐标轴上的值，削减为0的值，即可完成降维操作；

 

 

 

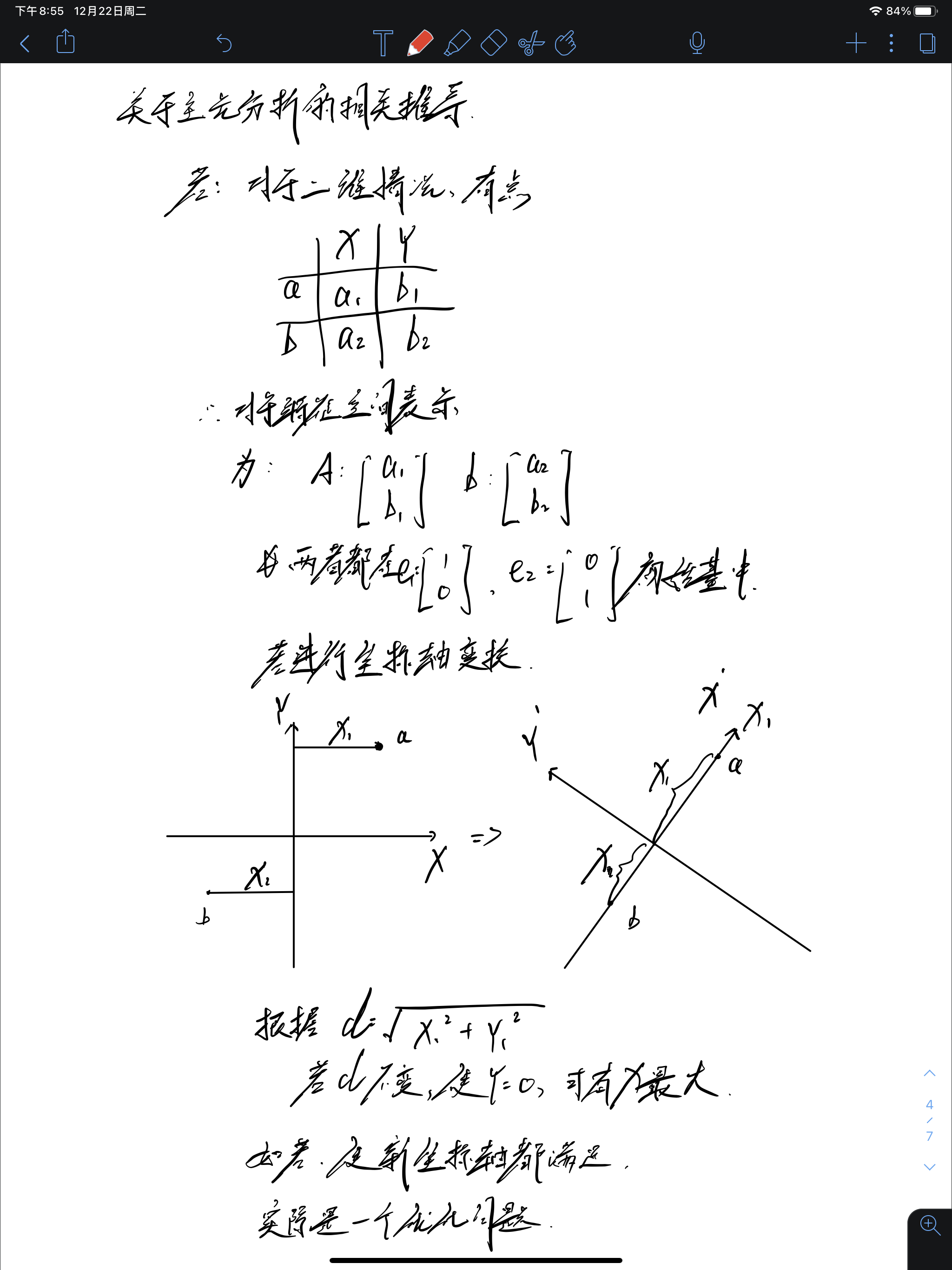
 从上述数学推导很轻松的看出来，寻找新基的过程其实就是做奇异值分解的过程；

 

 

 PCA主成分析实际操作：

 

 

所以可以看到，所谓的主成分析的主成分，就是找奇异值大的对应的特征向量，作为基进行表示；

 

【注意问题】：

但是值得注意的是，实际操作中，舍弃的都是比较小的特征值，特征值也不一定全为0；

特征值越小，代表该方向所贡献的信息量越少，所以舍弃也就越无伤大雅；

 

所以可以说，PCA主成分析，就是借助协方差矩阵（也可以不借助，直接采用点积得到的矩阵进行分解），进行特征值分解，从而进行特征向量的舍弃，完成降维操作；