【PAT甲级】1020 Tree Traversals (25分):树的创建、遍历
1020 Tree Traversals (25分)
Suppose that all the keys in a binary tree are distinct positive integers. Given the postorder and inorder traversal sequences, you are supposed to output the level order traversal sequence of the corresponding binary tree.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the postorder sequence and the third line gives the inorder sequence. All the numbers in a line are separated by a space.
Output Specification:
For each test case, print in one line the level order traversal sequence of the corresponding binary tree. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the end of the line.
Sample Input:
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
Sample Output:
4 1 6 3 5 7 2
分析:树的创建、遍历
题意:给你后序、中序序列,输出层次遍历序列。
- 总记不清创建左右子树时,后序序列的下标
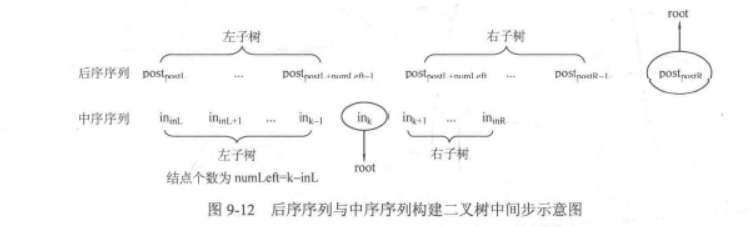
记住这个图
左子树记忆:假如左子树只有一个结点 postL=postL+leftNum-1=0
//左子树
Node->lchild=create(postL,postL+leftNum-1,inL,k-1);
//右子树
Node->rchild=create(postL+leftNum,postR-1,k+1,inR);
- 层序遍历的队列元素类型是node*不是node
代码
#include<iostream>
#include<queue>
using namespace std;
const int maxN=35;
int post[maxN],in[maxN];
int N;
struct node {
int data;
node* lchild;
node* rchild;
};
//用后序和中序序列构造二叉树
node* create(int postL,int postR,int inL,int inR) {
if(postL>postR) {//递归边界
return NULL;
}
node* Node=new node();
Node->data=post[postR];
//在中序序列中,查找in[k]==post[postR]的节点
int k=inL;
for(; k<=inR; k++) {
if(in[k]==post[postR])
break;
}
int leftNum=k-inL;//左子树的结点个数
//左子树
Node->lchild=create(postL,postL+leftNum-1,inL,k-1);
//右子树
Node->rchild=create(postL+leftNum,postR-1,k+1,inR);
return Node;
}
//层序遍历
int num=0;
void levelTra(node* root) {
queue<node*> que;
que.push(root);
while(!que.empty()) {
node* top=que.front();
que.pop();
printf("%d",top->data);
num++;
if(num<N) printf(" ");
if(top->lchild!=NULL) que.push(top->lchild);
if(top->rchild!=NULL) que.push(top->rchild);
}
}
int main() {
scanf("%d",&N);
for(int i=0; i<N; i++) {
scanf("%d",&post[i]);
}
for(int i=0; i<N; i++) {
scanf("%d",&in[i]);
}
//构造二叉树
node* root=create(0,N-1,0,N-1);
//输出层序序列
levelTra(root);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号