软工作业2： 论文查重

软件工程	https://edu.cnblogs.com/campus/gdgy/CSGrade21-34
作业要求	https://edu.cnblogs.com/campus/gdgy/CSGrade21-34/homework/13023
作业目标	按软件设计开发流程设计实现论文查重程序

 

GitHup地址

PSP表格：

PSP2.1	Personal Software Process Stages	预估耗时（小时）	实际耗时（小时）
Planning	计划	48	5
Estimate	估计这个任务需要多少时间	2	3
Development	开发	12	24
Analysis	需求分析（包括学习新技术）	8	10
Design Spec	生成设计文档	4	3
Design Review	设计复审	4	6
Coding Standard	代码规范（为目前的开发制定合适的规范）	4	6
Design	具体设计	8	12
Coding	具体编码	8	6
Code Review	代码复审	2	4
Test	测试（自我测试，修改代码，提交修改）	12	27
Reporting	报告	4	5
Test Report	测试报告	6	4
Size Measurement	计算工作量	3	5
Postmortem&Process Improvement Plan	事后总结，并提出过程改进计划	4	2
.	合计	129	120

 

假设序列S和T的长度分别为m和n, 两者的编辑距离表示为dp[m][n]. 则对序列进行操作时存在以下几种情况:

a.当S和T的末尾字符相等时, 对末尾字符不需要进行上述定义操作中(亦即"编辑")的任何一个, 也就是不需要增加计数. 则满足条件: dp[m][n] = dp[m-1][n-1].

b. 当S和T的末尾字符不相等时, 则需要对两者之一的末尾进行编辑, 相应的计数会增加1.

b1. 对S或T的末尾进行修改, 以使之与T或S相等, 则此时dp[m][n] = dp[m - 1][n - 1] + 1;
b2. 删除S末尾的元素, 使S与T相等, 则此时dp[m][n] = dp[m - 1][n] + 1;
b3. 删除T末尾的元素, 使T与S相等, 则此时dp[m][n] = dp[m][n - 1] + 1;
b4. 在S的末尾添加T的尾元素, 使S和T相等, 则此时S的长度变为m+1, 但是此时S和T的末尾元素已经相等, 只需要比较S的前m个元素与T的前n-1个元素, 所以满足dp[m][n] = dp[m][n - 1] + 1;
b5. 在T的末尾添加S的尾元素, 使T和S相等, 此时的情况跟b4相同, 满足dp[m][n] = dp[m - 1][n] + 1;

c. 比较特殊的情况是, 当S为空时, dp[0][n] = n; 而当T为空时, dp[m][0] = m; 这个很好理解, 例如对于序列""和"abc", 则两者的最少操作为3, 即序列""进行3次插入操作, 或者序列"abc"进行3次删除操作.

 

模块实现

Leven类中重要的函数：

• float getED(wstring str1, wstring str2, int len1, int len2);//用于计算句子最小编辑距离。

• void SentenceToOne();//循环按行文本读入，调用getED函数并将值压入vector ansArray中。

• wstring UTF8ToUnicode(const string& str);//UTF-8文件读入数据流并转换成Unicode编码，有利于提高运行效率以及准确率。

main函数：

int main(int argc,char* argv[]) {  //argc为参数个数，命令行中文件路径会存在argv中。

	if (check(argc, argv)) {
		Leven leven;
		leven.init(argc,argv); 
		leven.Run();
	}
	
	system("pause");
	return 0;
}

检查命令行参数：

bool check(int argc, char* argv[]) {  //检查命令函参数
	if (argc != 4) {
		cout << "ERROR:参数错误！\n";
		return false;
	}
	if (_access(argv[1], 00) == -1 || _access(argv[2], 00) == -1) {
		if (_access(argv[1], 00) == -1) cout << "Refer Adress Error\n";
		if (_access(argv[2], 00) == -1) cout << "Test Adress Error\n";
		return false;
	}
	return true;
}

经典DP算法：

float Leven::getED(wstring str1, wstring str2, int len1, int len2) {
	int temp;
	vector<vector<int>> dp(len1+1, vector<int>(len2+1));//len1行len2列的二维数组，记录状态值。
	//初始化
	for (int i = 1; i <= len1; i++) {  //例dp[2][0]表示一个长度为2的字符串str1与一个空字符串str2的最小编辑距离为2。
		dp[i][0] = i;
	}
	for (int j = 1; j <= len2; j++) {
		dp[0][j] = j;
	}
	for (int i = 1; i <= len1; i++) {
		for (int j = 1; j <= len2; j++) {
			if (str2[j - 1] == str1[i - 1])
				dp[i][j] = dp[i - 1][j - 1];
			else {
				temp = min(dp[i][j - 1], dp[i - 1][j]);
				dp[i][j] = min(temp, dp[i - 1][j - 1]) + 1;  //因为不一样所以会在最小结果上+1
			}
		}
	}
	return dp[len1][len2];
}

 

性能测试

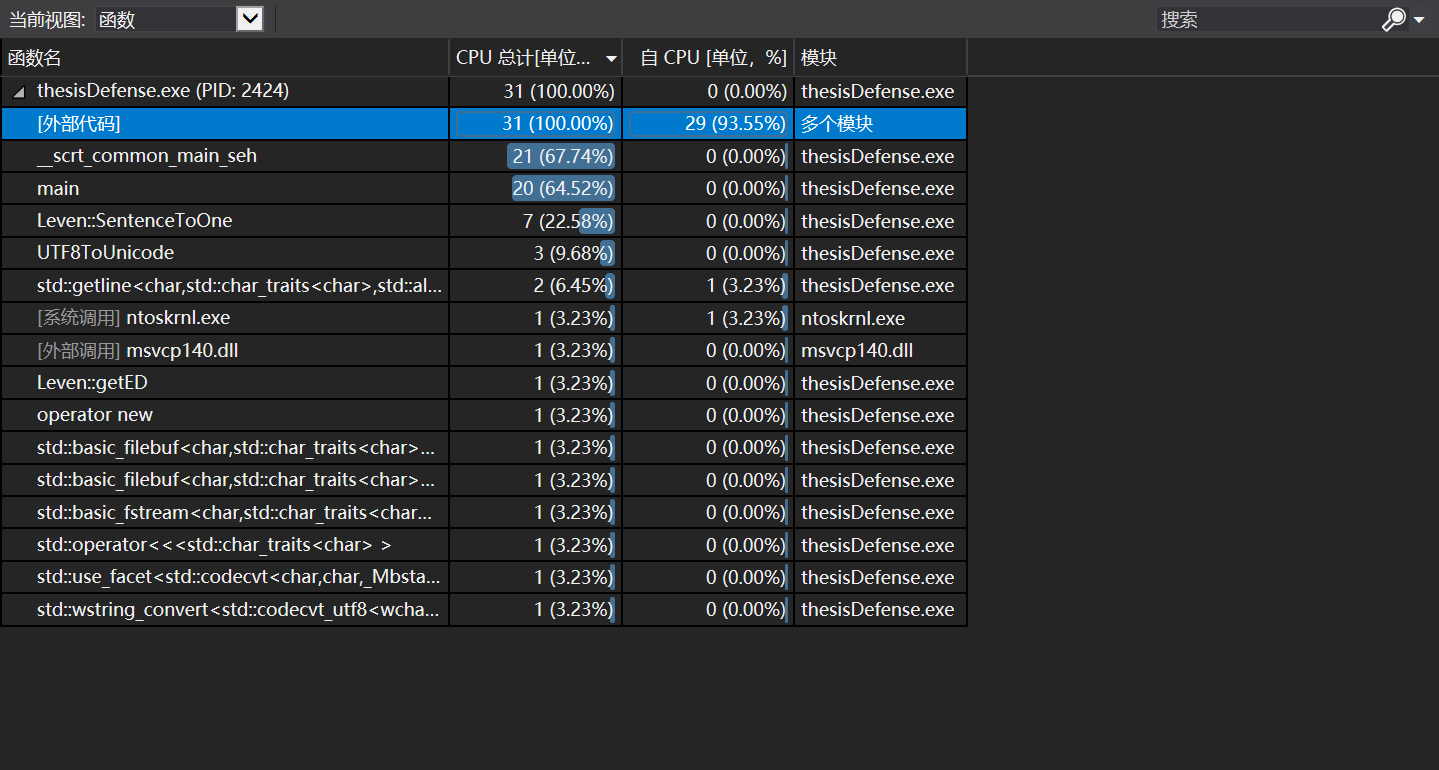
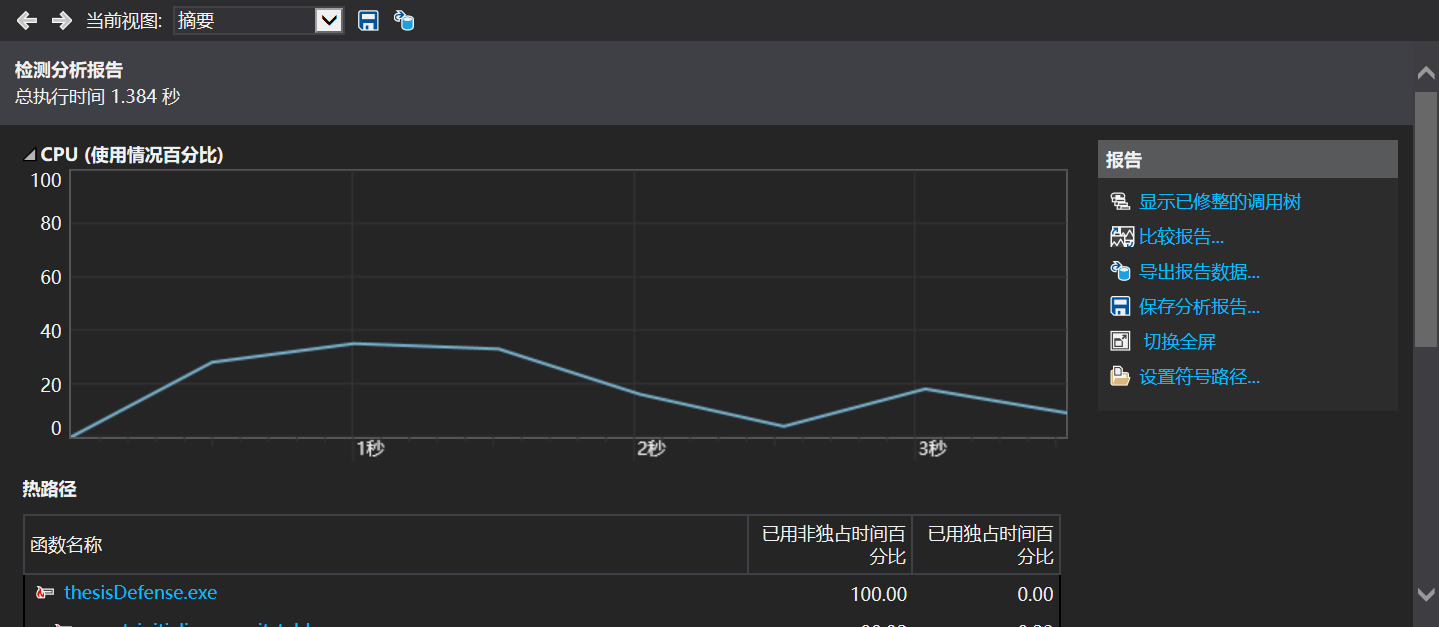
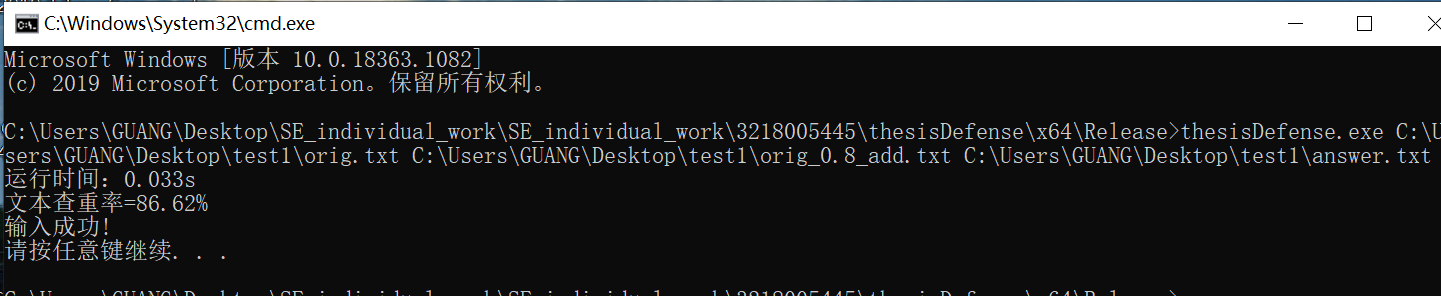
运行结果展示

单元测试

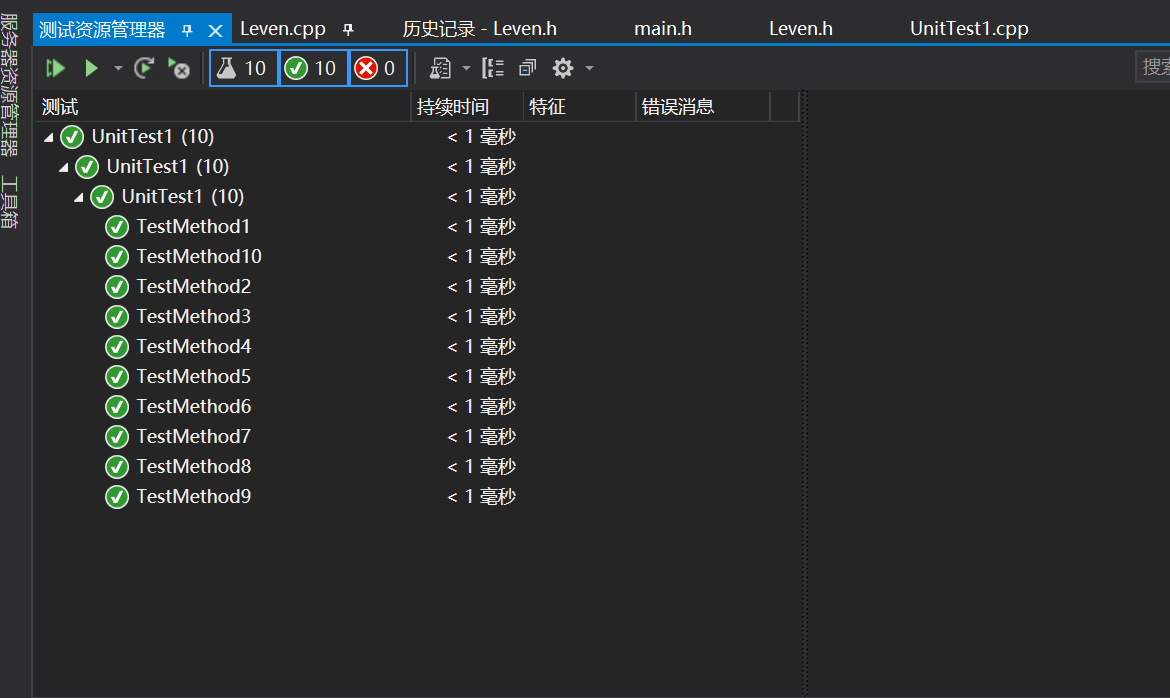
测试最小编辑距离，由于汉字的比较较难判断，因此都由英文、空格、逗号等代替。

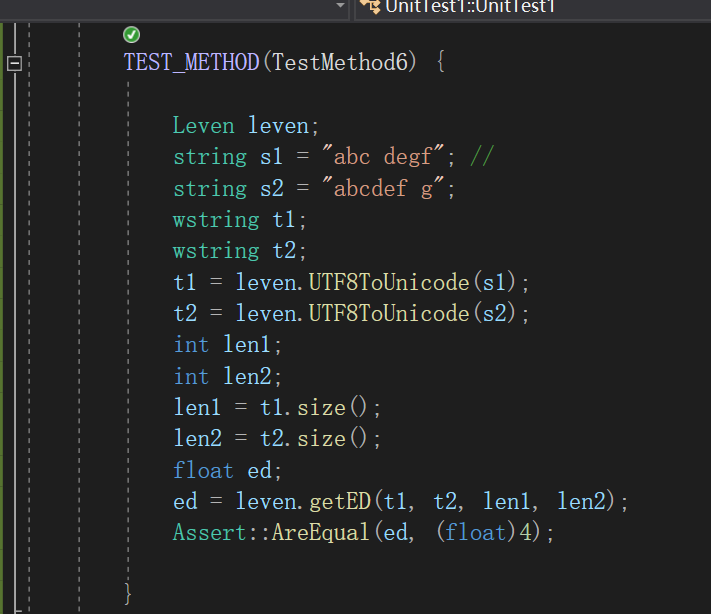
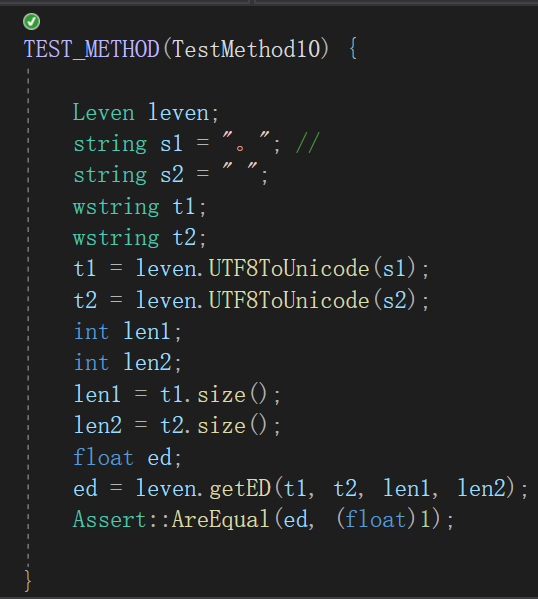
异常处理

处理命令行输入异常：输入参数个数不对、输入路径不可访问。

bool check(int argc, char* argv[]) {  //检查命令函参数
	if (argc != 4) {
		cout << "ERROR:参数错误！\n";
		return false;
	}
	if (_access(argv[1], 00) == -1 || _access(argv[2], 00) == -1) {
		if (_access(argv[1], 00) == -1) cout << "Refer Adress Error\n";
		if (_access(argv[2], 00) == -1) cout << "Test Adress Error\n";
		return false;
	}
	return true;
}

库函数可能发生异常，所以要捕获。

wstring Leven::UTF8ToUnicode(const string& str) {  //进行文本编码转换，以加强准确度。
	wstring ans;
	try {
		wstring_convert< codecvt_utf8<wchar_t> > wcv;
		ans = wcv.from_bytes(str);
	}
	catch (const exception& e) {
		cerr << e.what() << endl;
	}
	return ans;
}