二叉树：基于递归/非递归的前序遍历，中序遍历，后序遍历和层序遍历

用C/C++编写二叉树的前序遍历，中序遍历，后序遍历（递归）

使用辅助队列的层序遍历（非递归）

使用辅助栈的非递归先序，中序和后序遍历

特别说明一下层次遍历：借助一个队列，先将二叉树根结点入队，然后出队，访问出队结点，若它有左子树，则将左子树根结点入队；若它有右子树，则将右子树树根结点入队。然后出队，访问出队结点.......如此反复，直至队列为空

#include <iostream>
#include<string>
#define MAX 99
using namespace std;

typedef struct BiTNode {//二叉树结构体
    int data;
    struct BiTNode* lchild, * rchild;
}BiTNode, * BiTree;

typedef struct LinkNode {//下边两个结构体是队列
//由于下一行用到了BiTree结构体，所以应该把二叉树结构体BiTNode放在前，队列结构体放在后，否则VS2019报错
    BiTree tree;
    struct LinkNode* next;
};
typedef struct LinkQueue { 
    LinkNode* front, * rear;
};

typedef struct ListStack {//数据类型为BiTree的链式栈
    BiTree tree;
    ListStack* next;
}ListStack,*LStack;
void initStack(LStack& s) //链式栈的初始化
{
    s = (LStack)malloc(sizeof(ListStack));
    s->next = NULL;
}
void delectBiTree(BiTree& t)
{
    if (t)
    {
        //cout << "delelct " << t->data;
        delectBiTree(t->lchild);
        delectBiTree(t->rchild);
//这行不能与下行换位置，写delectAllSubTree花了快一个小时检查出来这个错
        t = NULL;
        free(t);
    }
}
bool isStackEmpty(LStack s) //判断链式栈是否为空
{
    return s->next == NULL ? true : false;
}
void Push(LStack& s, BiTree t)//将BiTree结点入栈
{
    ListStack* l = (ListStack*)malloc(sizeof(ListStack));
    l->tree = t;
    l->next = s->next;
    s->next = l;
}
void GetTop(LStack s,BiTree &p)//获取链式栈的栈顶元素，非出栈
{
    //cout << s->next->tree->data << endl;
    p=s->next->tree;
}
int GetStackDepth(LStack s)
{
    int count = 0;
    while (s->next)
    {
        s = s->next;
        count++;
    }
    return count;
}
void Pop(LStack& s,BiTree &t) //链式栈出栈，令t指向出栈元素
{
    LStack l;
    if (s->next == NULL) t = NULL;
    l = s->next;
    s->next = l->next;
    t = l->tree;
    free(l);
}
void initQueue(LinkQueue& q) //初始化链式队列
{
    q.front = q.rear = (LinkNode*)malloc(sizeof(LinkNode));
    q.front->next = NULL;
}
bool isEmpty(LinkQueue q) //判断链式队列是否为空
{
    return q.front == q.rear ? true : false;
}
void EnQueue(LinkQueue& q, BiTree t)//入队
{
    //cout << "this is EnQueue:" << t->data <<",lchild:"<<t->lchild->data<<",rchild:"<<t->rchild->data<< endl;
    LinkNode* p = (LinkNode*)malloc(sizeof(LinkNode));
    p->tree = t;
    p->next = NULL;
    q.rear->next = p;
    q.rear = p;
    //cout << "in " << t->data << endl;
}
BiTree DeQueue(LinkQueue& q) //队头元素出队，返回值为队头元素
{
    BiTree t;
    if (q.rear == q.front) return NULL;
    LinkNode* p = q.front->next;
    t = p->tree;
    //cout << endl;
    //cout << "quit " << t->data << endl;
    q.front->next = p->next;
    if (q.rear == p) q.rear = q.front;
    //这里不要写成q.front=q.rear，感谢Mr.SunShine帮我改bug，
    free(p);
    return t;
}

BiTree init()//先序输入一个二叉树，输入0代表该树为空
{
    int dat;
    cin >> dat;
    if (dat == 0) return NULL;
    else
    {
        BiTree t = (BiTree)malloc(sizeof(BiTNode));
        t->data = dat;
        t->lchild = init();
        t->rchild = init();
        return t;
    }
}
void PreOrder(BiTree t)//先序遍历
{
    if (t != NULL)
    {
        cout << t->data << " ";
        PreOrder(t->lchild);
        PreOrder(t->rchild);
    }
}

void InOrder(BiTree t)//中序遍历
{
    if (t != NULL)
    {
        InOrder(t->lchild);
        cout << t->data << " ";
        InOrder(t->rchild);
    }
}
void InorderWithoutRecursion(BiTree t)//中序非递归遍历二叉树，用栈辅助
{
    LStack s;
    initStack(s);
    BiTree p = t;
    while (p || !isStackEmpty(s))
    {
        if (p!=NULL)
        {
            //cout <<"push"<<p->data << endl;
            Push(s, p);
            p = p->lchild;
        }
        else
        {   
            Pop(s,p);
            cout <<" "<< p->data;//若为先序非递归遍历，则只需把此行放到if段的末尾
            p = p->rchild;
        }
    }
}
void PostOrder(BiTree t)//后序遍历
{
    if (t != NULL)
    {
        PostOrder(t->lchild);
        PostOrder(t->rchild);
        cout << t->data << " ";
    }
}
void PostOrderWithoutRecursion(BiTree t)//后序非递归遍历二叉树，用栈辅助
/*
用一个辅助指针r来标记最近访问过的结点
1.沿着根结点的左孩子，依次入栈，直到左孩子为空
2.读入栈顶元素（不是出栈），若其右孩子不空且未被访问过
  将右子树转执行.1.；否则，栈顶元素出栈并访问
*/
{
    LStack s;
    BiTree p=t,r=NULL;
    initStack(s);
    while (p || !isStackEmpty(s))
    {
        if (p)
        {
            Push(s, p);
            p = p->lchild;
            //cout << "i am here " << GetStackDepth(s) << endl;;
        }
        else {
            GetTop(s, p);
            if (p->rchild && p->rchild != r)
            {
                p = p->rchild;
//  个人感觉以下两行代码不写也可以，无非要多循环几次
                Push(s, p);     
                p = p->lchild;
            }
            else
            {
                Pop(s, p);
                cout << " " << p->data;
                r = p;
                p = NULL;
            }
        }
    }
}
void LevelOrder(BiTree t)//层序遍历，用队列辅助
{
    LinkQueue q;
    initQueue(q);
    BiTree temp;
    if (t == NULL) {
        cout << "树为空" << endl;
    }
    else
    {
        EnQueue(q, t);
        while (/*temp||*/!isEmpty(q))
        /*
        如果为while(p||!isEmpty(q)) 则要在最后把p修改为NULL
        否则最后一步出栈二叉树的最右下元素后，p非空，但队列为空
        还会继续循环一次使Dequeue报错
        */
        {
            temp = DeQueue(q);
            cout << temp->data << " ";
            if (temp->lchild != NULL)
            {
                EnQueue(q, temp->lchild);
            }
            if (temp->rchild != NULL)
            {
                EnQueue(q, temp->rchild);
            }
            //temp = NULL;
        }
    }
}
/****************************************************************/
int findDepth(BiTree t)
{
    if (!t) return 0;
    else
        return findDepth(t->lchild) + 1 > findDepth(t->rchild) + 1 ? findDepth(t->lchild) + 1 : findDepth(t->rchild) + 1;
}
int findDepthWithoutRecusion(BiTree t)
//用的是非递归前序/中序遍历算法,也可用层次遍历并设置变量记录当前层数
{
    int maxDepth = 0;
    LStack s;
    initStack(s);
    BiTree p=t;
    while (p || GetStackDepth(s))
    {
        if (p)
        {
            Push(s, p);
            p = p->lchild;
            if (maxDepth < GetStackDepth(s))
                maxDepth = GetStackDepth(s);
        }
        else
        {
            Pop(s, p);
            p = p->rchild;
        }
    }
    return maxDepth;
}
int sumNode(BiTree t)
{
    if (!t) return 0;
    else
        return sumNode(t->lchild) + sumNode(t->rchild)+1;
}
/********************************************************************/
int isCBTree(BiTree t)//判断树是否为完全二叉树
//遇到空结点时，查看其后是否还有非空结点，若有，则不是完全二叉树
{
    LinkQueue q;
    initQueue(q);
    BiTree p = t;
    EnQueue(q, p);
    while (!isEmpty(q))
    {
        p=DeQueue(q);
        if (p)
        {
                EnQueue(q, p->lchild);
                EnQueue(q, p->rchild);
        }
        else
        {
            while (!isEmpty(q))
            {
                p=DeQueue(q);
                //cout << " " << p->data << endl;
                if (p) 
                    return 0;
            }
        }
    }
    return 1;
}
static int predt = -1;
int isBSTree(BiTree t)//用中序遍历递增的条件
{
    int b1, b2;
    if (t == NULL) return 1;
    else
    {
        b1 = isBSTree(t->lchild);
        if (b1 == 0 || predt >= t->data) return 0;
        predt = t->data;
        b2 = isBSTree(t->rchild);
        return b2;
    }
}
void swapLR(BiTree &t)
//交换树的全部左右子树，思路类似后序递归遍历
{
    if (t)
    {
        swapLR(t->lchild);
        swapLR(t->rchild);
        BiTree temp = t->rchild;
        t->rchild = t->lchild;
        t->lchild = temp;
    }
}
BiTree findParentByData(BiTree t, int e)
//用后序遍历找到结点，此时栈内按输出顺序依次为祖先
{
    LStack s;
    initStack(s);
    BiTree p = t,r=NULL;
    BiTree bi[MAX];
    while (p || !isStackEmpty(s))
    {
        //cout << "p = " << p->data << endl;
        if (p)
        {
            Push(s, p);
            p = p->lchild;
        }
        else {
            GetTop(s, p);
            if (p->rchild && p->rchild != r)
            {
                p = p->rchild;
            }
            else {
                Pop(s, p);
                if (p->data == e)//这里才是主要答案
                {
                    /*获取整个祖先路径
                    while (s->next != NULL)
                    {
                        cout << "_" << s->next->tree->data;
                        s = s->next;
                    }
                    return;
                    */
                    //下一行是获取直接祖先
                    return s->next->tree;
                }
                r = p;
                p = NULL;
            }
        }
    }
    return NULL;
}
void delectAllSubTrees(BiTree& t, int e)//删除树中值为e的结点的子树
//由于树中可能有多个值相同的结点，所以用层次遍历
{
    BiTree bi[MAX];
    LinkQueue q;
    initQueue(q);
    BiTree p = t;
    EnQueue(q, p);
    BiTree pre = NULL;
    while (!isEmpty(q))
    {
        p=DeQueue(q);
        if (p)
        {
            //cout << " p=" << p->data << endl;
            if (p->data == e)
            {
//delectBitree函数会把根结点也删除，所以要额外保存/创建一个一样的根结点，执行完delectBitree后
//再把此根结点和它的父结点连接上
                //cout << "找到结点p=" << p->data << endl;
                BiTree temp=(BiTree)malloc(sizeof(BiTree));//建立一个结点备份执行delectBitree的根结点
                temp->data = e;
                temp->lchild = NULL;
                temp->rchild = NULL;
                BiTree parent=findParentByData(t, e);//查找出此结点的父结点
/*findParentByData是通过结点的值查找结点的父母，也就决定了它只能应用到结点数值无重复的情况中，
否则会出现第二个相同值的结点子树无法删除的情况，这是因为第二个结点的父母判断错了，
函数认为它的父母还是第一个结点的父母*/
                //cout << "父母是" << parent->data << endl;
                if (parent->lchild == p)//判断父子关系
                {
            //        cout << "左孩子" << endl;
                    delectBiTree(p);
                    parent->lchild = temp;//连接父子
                }
                if (parent->rchild == p)
                {
                //    cout << "右子树" << endl;
                    delectBiTree(p);
                    parent->rchild = temp;
                }
                p = temp;//还原执行前的结点,不还原会出错                
            }
            if (p->lchild!=NULL) EnQueue(q, p->lchild);
            if (p->rchild!=NULL) EnQueue(q, p->rchild);
        }
    }
}
 
int findWidth(BiTree t)
{
    LinkQueue q;
    initQueue(q);
    BiTree p = t;
    BiTree pre = p;
    EnQueue(q,p);
    int nodeHight = 1, width=1;
    int maxWidth = 0;
    while (!isEmpty(q))
    {
        p=DeQueue(q);
        if (maxWidth < width) maxWidth = width;
        //cout <<"nodeHight="<<nodeHight<< " p=" << p->data << " pre=" << pre->data << " width=" << width << endl;
        if (p == pre)
        {
            width = 1;
            nodeHight++;
        }
        else 
            width++;
        if (p)
        {
            if (p->lchild) EnQueue(q, p->lchild);
            if (p->rchild)
            {
                EnQueue(q, p->rchild);
                if(p==pre)
                pre = p->rchild;
                //cout << "pre=" << pre->data << endl;
                //cout << "width=" << width << endl;
            }
        }
    }
    return maxWidth;
}
/********************************************************/
int main(void)
{
    cout << "前序输入二叉树，0代表空结点："<<endl;
    BiTree t = init();//建立二叉树，并输入
    /*
    cout << "递归求树的高度："<<findDepth(t)<<endl;
    cout << "非递归求树的高度：" << findDepthWithoutRecusion(t)<<endl;
    cout << "递归求树的结点数：" << sumNode(t) << endl;
    */
    /*
    string l=isCBTree(t) == 1 ? "是完全二叉树" : "不是完全二叉树";
    cout << l << endl;

    string str=isBSTree(t) == 1 ? "是排序二叉树" : "不是排序二叉树";
    cout << l << endl;

    swapLR(t); //交换全部左右子树

    findParentByData(t, 7); //找结点全部祖先
    delectAllSubTrees(t, 2);//删除值为e的结点的子树
    findWidth(t);//求树的宽度，即有结点数最多的那一层的个数
    */
    /*
    cout << "前序遍历：";
    PreOrder(t);
    cout << endl;
    cout << "中序遍历：";
    InOrder(t);
    cout << endl;
    cout << "非递归中序遍历：";
    InorderWithoutRecursion(t);
    cout << endl;
    cout << "后序遍历：";
    PostOrder(t);
    cout << endl;
    cout << "非递归后序遍历：";
    PostOrderWithoutRecursion(t);
    cout << endl;
    cout << "层次遍历：";
    LevelOrder(t);
    cout << endl;
    */
}

 

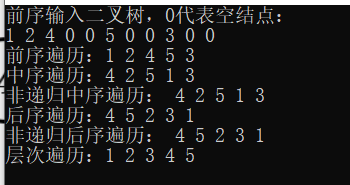
前序输入二叉树：0表示结点为空NULL，1 2 4 0 0 5 0 0 3 0 0 

 

运行：