Manacher线性求解所有极长回文串的区间答案

之前打模拟赛见到的trick。
例题：给出一个长为n的序列A，求解对于每个位置为中心的最长回文串内的数字种类数（包括偶回文）。
首先manacher可以求最长回文串，我们考虑怎么顺便求数字种类数。

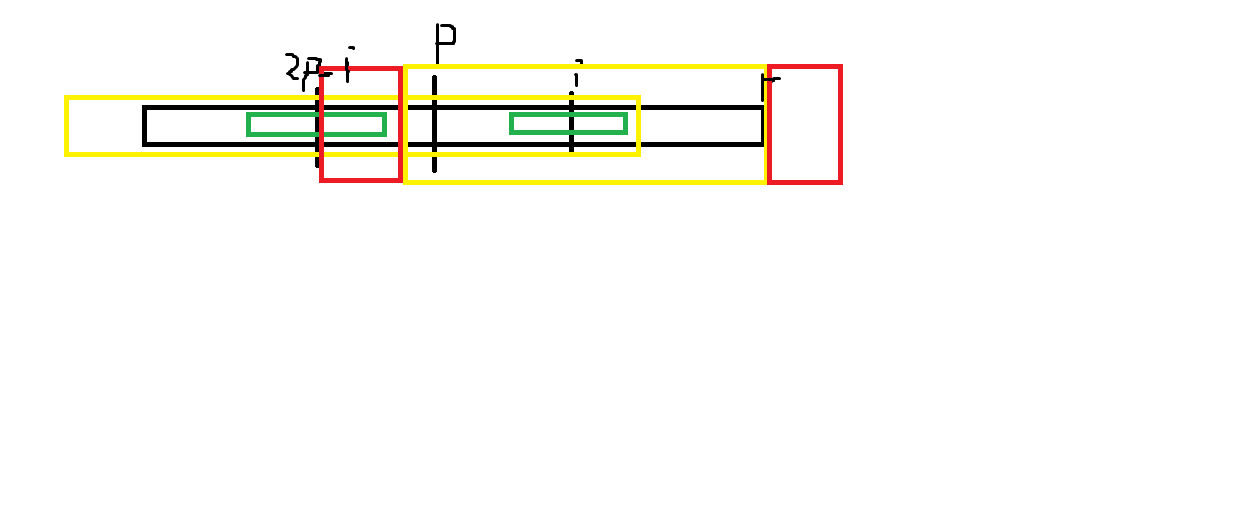
我们将答案的转移分两类。如果2p-i处最长回文没有超过左边界2p-r处，那么\(ans_i\)就可以直接等于\(ans_{2p-i}\)（绿色）。如果超过了（黄色），那么就暴力地像莫队一样缩回去，也即从\(ans_{2p-i}\)为起点，逐步扣除两端的贡献直到包含进左端点以内。当然，缩了之后还有可能扩充（红色），就像manacher原算法那样。重点在于，只要需要缩减，无论是否扩充（红色部分是否存在），p都必须更新为i，否则复杂度分析将失效。
我们现在来证明这个看起来很暴力的东西是对的。我们设p到2p-i的距离是d1,2p-i到2p-r的距离是d2。那么显然r到2p-i的距离是2d1+d2，p到i的距离是d1。首先\(maxlen_{2p-i}\le 2d_1+d_2\)，因为超过了的话显然与p是右端点最右的点矛盾。其次本次缩减的代价是\(maxlen_{2p-i}-d_2\)，因此代价\(\le 2d_1\)。而我们注意到，每次造成贡献后，p必然向右移到i处，也即向右移了d1步。因此，总复杂度线性。
这个能处理的东西看起来比莫队少一点。比如其处理数字种类数问题时，扣除贡献的方式并非查看其已有出现次数（因为不可能维护每个回文串中每个数的出现次数），而是查看其lastpos或nextpos来处理。