(ISCA 2025) Chimera: Communication Fusion for Hybrid Parallelism in Large Language Models
(ISCA 2025) Chimera: Communication Fusion for Hybrid Parallelism in Large Language Models
针对大语言模型混合并行的通信融合
本文包括了笔者自行的学习和分析。非论文部分将标记出来。
摘要和背景
Why?
随着大模型规模的不断增大和摩尔定律的放缓,受到单个NPU内存的限制,LLM的训练需要使用混合并行的方式进行,这些混合并行方式引入了多样的集合通信方式。
Challenge?
频繁的阻塞式通信严重影响了多NPU系统的效率。
Solution?
为了解决这样的问题,文章提出了Chimera,一种通信融合机制,经过研究不同并行策略的通信进程,找到通信冗余部分,通过重排算子和生成无冗余的通信算子,减轻了混合并行中的瓶颈。
介绍
面临的挑战
- 不同的并行策略引入了不同的通信模式来保证NPU之间的同步,这导致了复杂的通信进程和严重的通信开销,并且挤占了大量的计算时间,因为计算需要等待通信。
- 混合并行模式,网络拓扑结构,硬件配置的多样性使得通用,灵活的通信优化更加具有挑战性。
现有的不足
现有的工作:
- 更加细粒度的核融合->减少相邻计算核通信操作的内存读取。
- 调度优化->提升计算和通信的交叠。
- 针对没有依赖的算子进行交叠,不影响其他算子。
- 对于相邻以来算子,通过PP来实现细粒度的并行。
没有考虑到:
- 通信进程自身在混合并行中的作用,无法解决挑战。
- 解决方式特化性强,不具有普遍性和泛化性。
背景
主要介绍并行策略和集合通信。参见附录。
动机
文章主要通过以下方式进行。
- 认识通信冗余
- 针对通信开销进行建模
- 针对不同的并行方式,对通信算子进行融合
- 评估
认识通信冗余
分析了Megatron:在TP+SP时可以通过前向reduce-scatter反向all-gather的算子融合实现,减少all-reduce开销。(all-reduce需要进行两次ring,reduce-scatter只需要进行一次ring)。
分析了S-Lora,将All-gather和All-reduce通过调整计算和通信顺序,减少一次通信开销。(实际上并没有减少,因为必然地baseline的Add操作需要等待All-reduce,All-reduce的时间开销大于All-gather,但是能够减少IDLE的时间占比)。
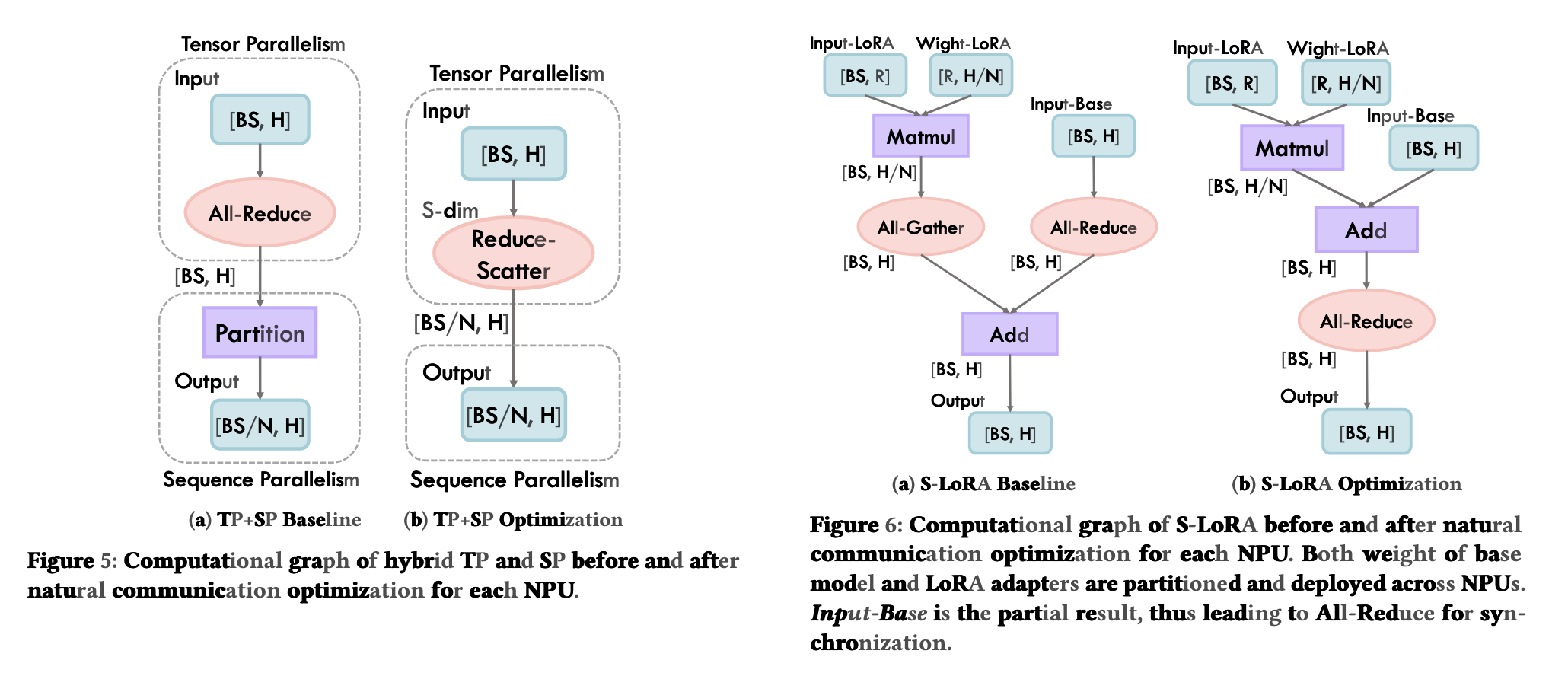
文章指出这些都是基于观察而没有进行系统性的定义,或者提供一个全局的方法来消灭这些这些通信冗余。
进行建模
根据并行的方式,我们可以对其进行建模。这里我们均考虑ring算法,这样我们就可以得到,设我们的并行度为t。我们可以得到:
| 并行方式 | 通信 | 开销 |
|---|---|---|
| TP | All-reduce | \(2(t-1)\times bsh/t\) |
| PP | P2P | \(bsh\) |
| SP | All-Gather | \((t-1)\times bsh/t\) |
| EP | All-to-All | \((t-1)\times bshk/t\) |
| SP | Reduce-scatter | \((t-1)\times bsh/t\) |
| / | Many-to-Many Scatter | \(bsh\) |
有关ring算法参见附录。
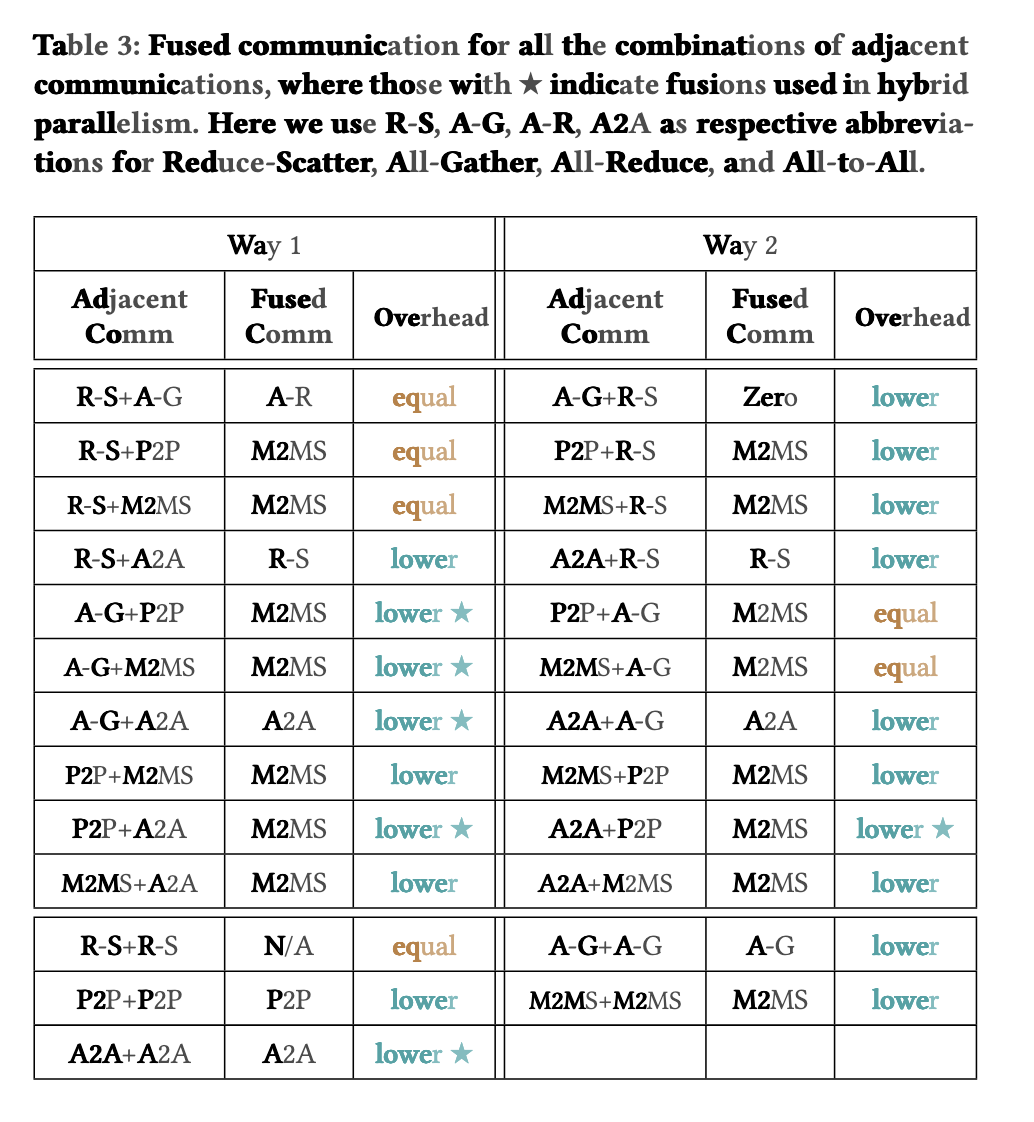
更进一步地衡量所有的混合并行算法的开销:

Chimera
- 将连续的并行策略产生的通信算子进行融合,从而生成必要的最简单的通信算子。
- 分为三步:
- 将All-Reduce分解成Reduce-Scatter+All-gather来进行更细粒度的算子融合。这样我们将会有R-S,A-G,A-A,p2p,M2MS五种基础的算子。
- 重排通信算子,让被计算算子分隔的通信算子相邻,从而更好实现通信融合。现有的并行策略,仅有MOE的gating算子需要通信算子的重排。
- 替代相邻算子成融合算子。
下图展示了融合算子的表现情况。
Case I: PP + EP

调整gating函数这样就可以融合P2P+all2all成为M2MS。
Case II: SP + EP + SP

重排+融合算子。
附录
有关并行策略,各个层的储存激励量分析,以及通信模式的分析
并行策略介绍(非论文部分)
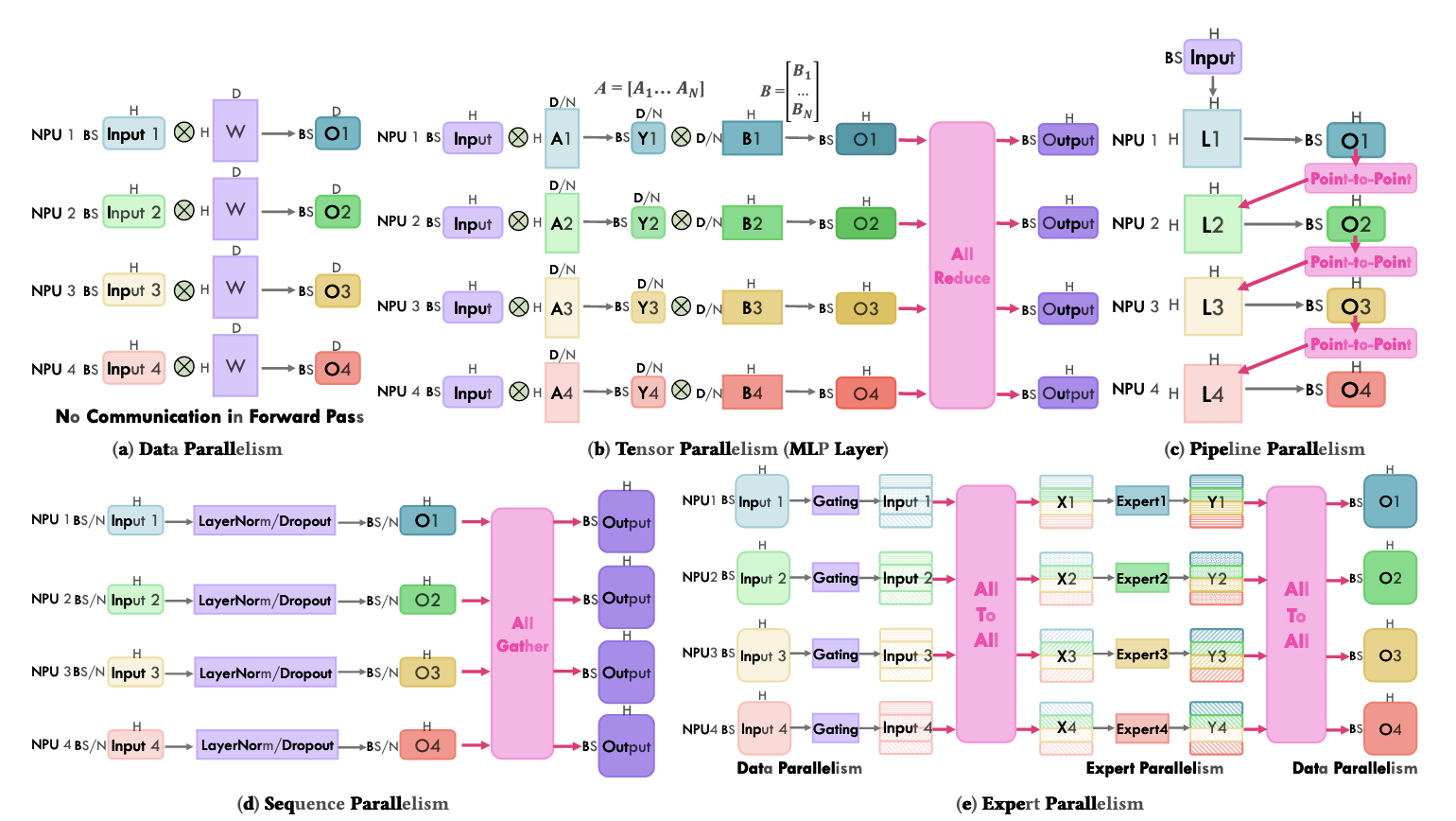
目前常用的并行策略分为数据并行(DP),张量并行(TP),流水线并行(PP),专家并行(EP),序列并行(SP),上下文并行(CP)等。受限于篇幅我们并不会非常详细地解释,只会简要介绍通信模式。
DP,TP,EP 在megatron LM中有详细介绍。笔者的学习:megatron LM
对于专家并行:专家并行最早来源于Gshard这篇论文,其中最为常用的通信为alltoall通信。

上下文并行(CP, context parallelism),主要也是针对不同rank上的运算。利用Q不变,KV流动或者Q流动,KV不变的方式,通过ring p2p attention的方式来获得运算的输出,一般用于推理,是序列并行的一种方式。

序列并行SP主要有两篇文章进行了介绍: Essay 1和Essay 2。两篇文章虽然都是序列并行但解决的侧重点有所不同。前者主要解决模型上下文过长的问题,后者主要解决模型的显存占用问题。
在文章一中,类似于CP,我们也采用ring p2p的方式传递K和V,Q不变。

而在Megatron中,原本的TP将只会在Attention层执行。通过将权重Tensor进行纵向切割,输入tensor不切割的方式减少显存占用。
而在序列并行中,Megatron注意到没有进行TP的区域,在sequence维度下操作是独立的。于是需要将输入到LayerNorm层和Dropout层前的张量沿着序列维度进行拆分,这样通信的方式就会变成:
前向:
... -> all-gather -> reduce-scatter -> all reduce -> all-reduce -> reduce-scatter -> all-gather -> ...
反向传播则与前向完全对偶。

这里文章给我们提供了一张完整的图。
有关激活量分析(非论文部分)
我们的模型,将会按照如下的方式来进行分析。通过了解激活量,我们能够更好了解通信开销。首先,我们定义如下的一些参考量。
| 参考量 | 意义 | 参考量 | 意义 |
|---|---|---|---|
| a | 注意力头数 | b | batch输出量 |
| h | 隐藏层维度 | l | transformer块数量 |
| p | 流水线层数 | s | 序列长度 |
| t | 张量并行度 | v | embedding维度 |
| d | FFN 线性变换维度 | k | 专家并行数 |
接下来,我们根据原论文图中经典的方式来对各个层进行激活量的分析。这里采用最经典的MHA模式,不考虑MQA,GQA,MLA等KVCache优化方式和NSA,DSA等主流稀疏化操作。这一部分参考来源于Essay 2。

Part 1: 输入前的预处理部分(Input Embeddings)
在输入时,我们的输入大小为 \(bsv\) 。输入嵌入层进行词嵌入操作(\(v\times h\))和位置编码(不改变维度)后,我们得到了进入Transformer块前的操作。这一部分可以通过预先处理完成,因此我们不需要计入到实际的Transformer激活量的计算中。这样,我们将会拥有一个 \(bsh\) 的输入,随后我们开始我们的计算。
Part 2: (LayerNorm + Attention)
这一部分我们正式进入Transformer块。
对于LayerNorm,我们需要保留激励用于方向传播。因此这里将出现 \(bsh\).
接着,我们将进入attention块中。首先我们将进行的就是self-attention模块,而这一部分我们将会有如下的结构。

- 对于投影矩阵变换,我们将需要 \(bsh\) 保存输入。
- 对于Q, K在执行 \(QK^T\) 前,我们需要 \(2bsh\) 的保存输入。
- 对于执行softmax前,我们需要保留 \(QK^T\in\mathbb{R}^{s\times s}\) 的输入。也就是我们需要保存 \(abs^2\) 的输入。
- 需要注意的是,在这里,Q和K首先会因为多头注意力的使用,使得每个头分配到一个 \(Q_i, K_i\in\mathbb{R}^{s\times \frac{h}{a}}\). 这样每个头的输出 \(Q_iK_i^T\in\mathbb{R}^{s\times s}\),而总共有 \(a\) 个头。
- Softmax 前的mask掩码,需要消耗 \(1/2 as^2b\) 空间。因为掩码将会遮蔽一半的输出。
- softmax输出和V相乘,需要消耗 \(as^2b + bsh\) 的空间。
- 最后线性层变换以及dropout,需要消耗 \(bsh + 1/2 bsh\) 的空间。
这样,在整个LayerNorm + attention模块,我们将需要 \(bsh + 11/2bsh + 5/2 abs^2 = 13/2bsh + 5/2 abs^2\) 大小的空间储存我们的激励。
Part 3: (LayerNorm + MLP)/(Moe)
这一部分是后面的FFN模块。
对于LayerNorm,我们需要保留激励用于方向传播。因此这里将出现 \(bsh\).
接着,我们按照标准的FFN模型进行计算。我们按照图中所示,设两层Linear分别将 h->d, 和将 d->h。
- 对于第一层Linear的输入,我们需要 \(bsh\) 的激活保存。
- 对于GELU输入,我们需要保存 \(bsd\) 的激活。
- 对于第二层Linear,我们需要保存 \(bsd\) 的激活。
- 对于DropOut,我们需要保存 \(1/2bsh\) 的掩码。
这样针对一个FFN模块,我们需要 \(5/2bsh + 2bsd\) 的激励需要存储。
对于Moe模块,我们将每一个Expert当作一个原先的FFN。这样,根据上面的计算,我们每一个FFN需要储存 \(3/2bsh + bsd\) 的大小。
首先,我们需要经过一层LayerNorm。这里我们将需要存储 \(bsh\)。
其次,我们需要将其通过一个门控网络。这里将会计算出来每个专家的权重。对于经典的gating,我们有:
- 与门函数线性层计算 输入 \(\mathbb{R}^{s\times h}\cdot\mathbb{R}^{h \times k} = \mathbb{R}^{s\times k}\),总共有K个专家。这样输入存储 \(bsh\)。
- softmax计算,将其转换成 \(k\times 1\) 的权重。这里存储需要 \(bsk\).
- k个专家的输入,我们需要存储k个权重和 \(kbsh\) 的数据。这里我们直接计做 \(k(5/2bsh + 2bsd)\)。
这样对于我们的Moe,我们需要 \(bsh + bsh + bsk + k(5/2bsh + 2bsd)\) 的权重计算。
这样我们就了解了相关的权重激励。
TP,SP对于权重的影响(非论文部分)
TP和SP
对于TP和SP,我们将具有相同的并行度t,并且在以下的层进行均分。我们具有如下的分割方式:
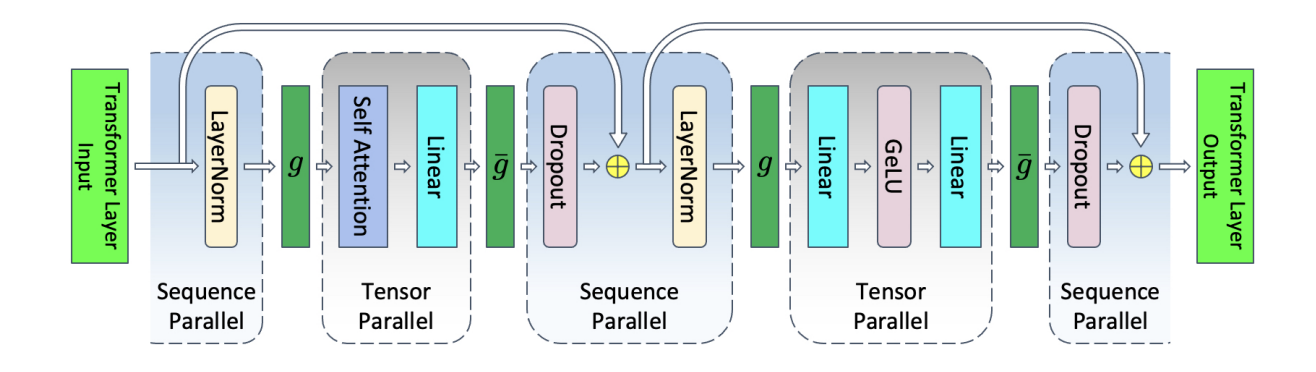
这样对于所有的Layernorm,Dropout,attention,FFN(Moe)部分都将拥有 \(t\) 的并行度。为此我们只需要将上面各个部分均除以 t 即可。需要注意的是,TP和SP的并行度虽然相同,但是切割方式不同,通信方式也完全不同。这里我们可以理解为:
- 数据切割类型的不同:SP针对输入数据在seq维度进行切分,模型的权重不变。TP针对模型权重进行切分,输入数据不变。
- 通信的方式不同。SP需要进行前向all-gather - reduce-scatter操作,反向对偶。TP需要进行all-reduce - all-reduce 操作,反向对偶。
有关通信模式分析
集合通信介绍(非论文部分)
我们此处提供所有的集合通信操作。
NCCL提供了8种集合通信操作:ncclAllReduce, ncclBroadcast, ncclReduce, ncclAllGather, ncclReduceScatter, ncclAlltoAll, ncclGather, ncclScatter.
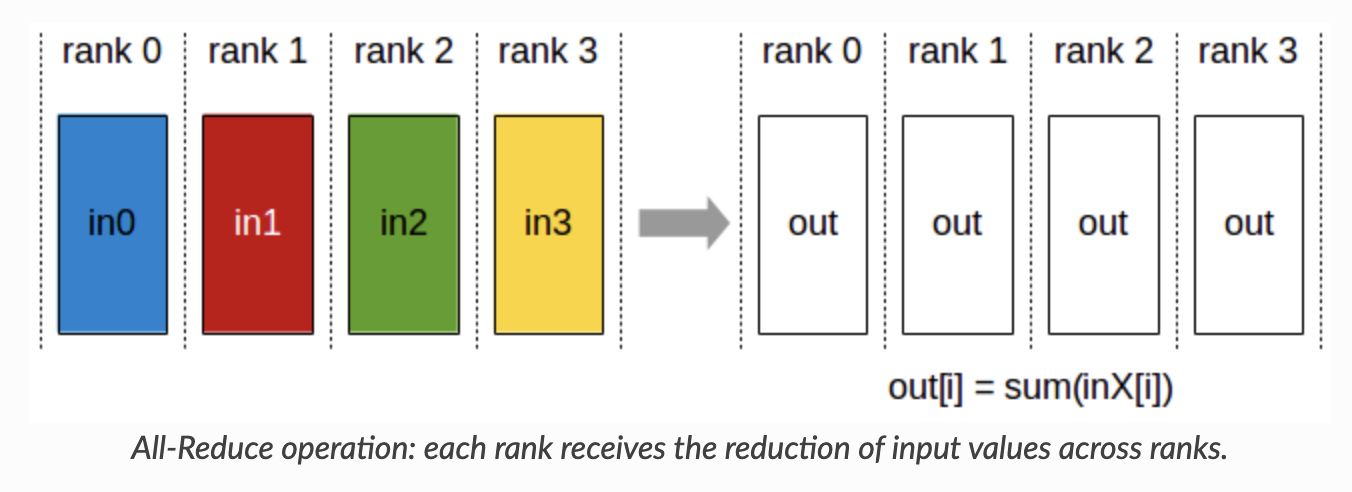
- All Reduce:
![img]()
- Broadcast:
![img]()
- Reduce:
![img]()
- AllGather:
![img]()
- ReduceScatter:
![img]()
- AlltoAll:
![img]()
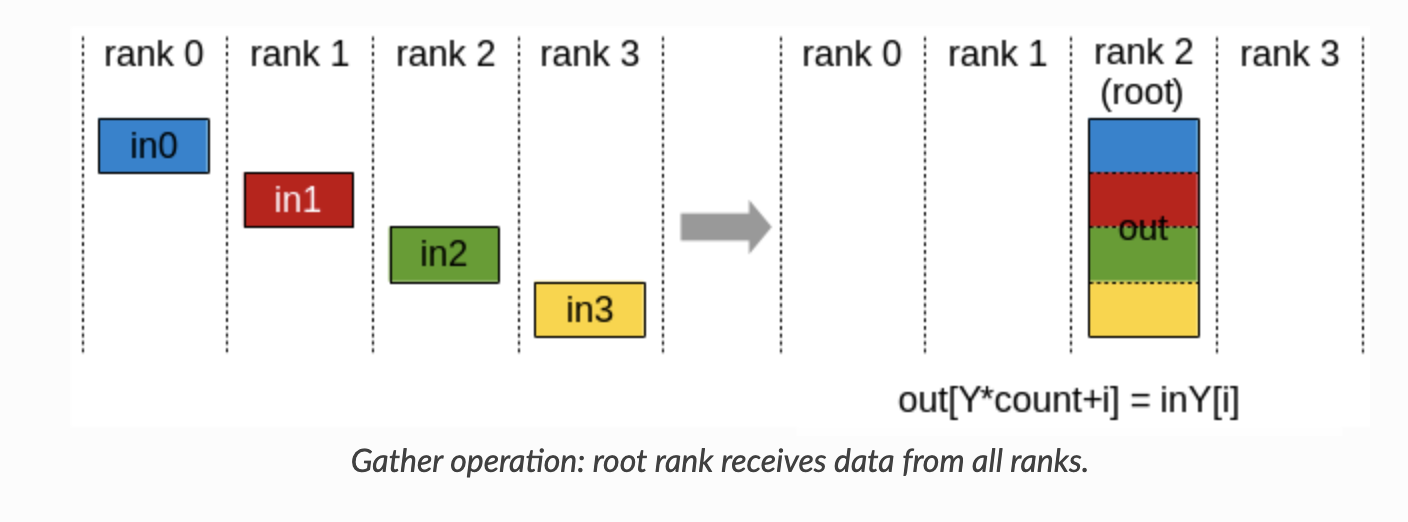
- Gather:
![img]()
- Scatter:
![img]()
除此之外,文章也介绍了p2p通信和many-to-many通信。这里我们只需要知道many-to-many scatter通信类似于矩阵转置即可。与all-to-all不同,many-to-many scatter并不是一个通信域内的通信,而是跨通信域的通信。
Megatron 部分(包含了作者自己的理解)
针对Megatron LM,这是一个DP,TP,PP,SP,EP的混合并行系统。在这之中,我们需要了解各个通信的通信方式。
- DP:数据通过broadcast到各个节点上,计算得出output后,在gather最终的输出结果。
- TP:数据通过计算后,all-reduce形成结果。
- PP:数据在各个rank之间通过p2p的方式进行传输。
- SP:数据进行切分后,通过all-gather后得到输出,在经过reduce-scatter得到最终结果。
- EP:All-to-All通信,需要将数据的每一部份都分给专家。
有关TP的通信模式解释如下图所示。

对于SP:我们有 g:
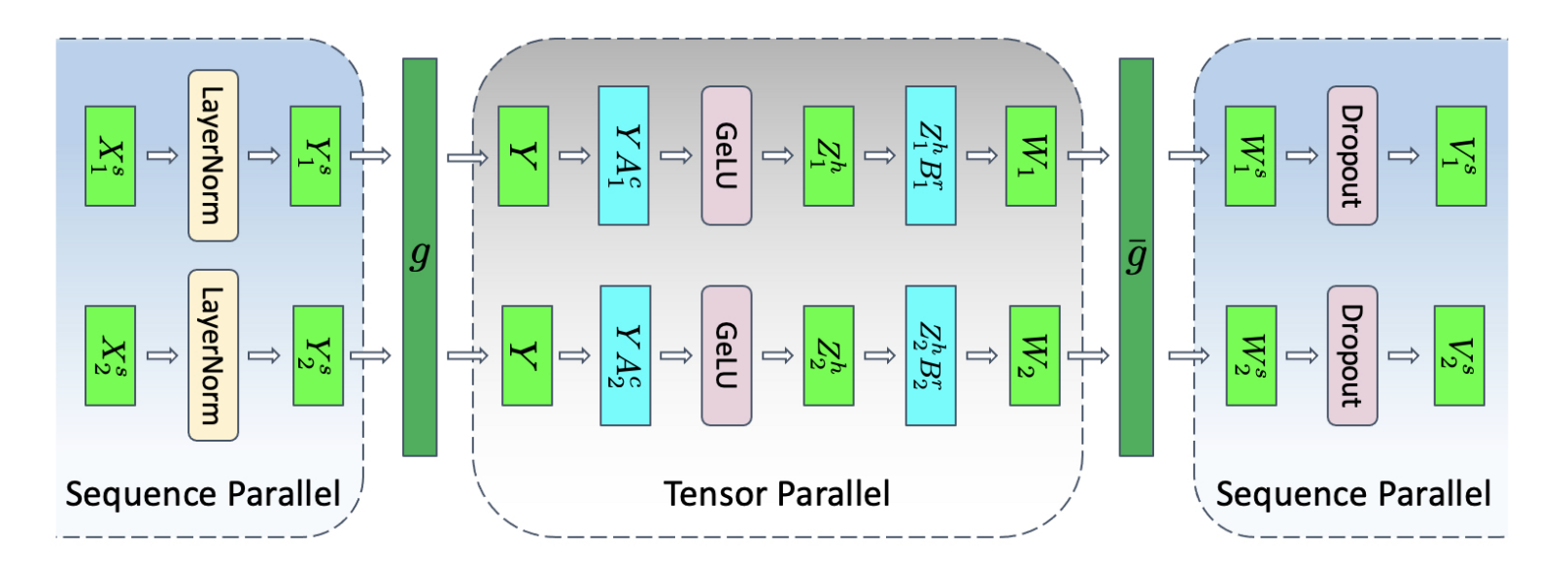
- 前向:\([Y, Y] = [[Y_1^s, Y_2^s], [Y_1^s, Y_2^s]]\) (all-gather)
- 反向:\([\dfrac{\partial L}{\partial Y_1^s}, \dfrac{\partial L}{\partial Y_2^s}] = [\dfrac{\partial (L_1 + L_2)}{\partial Y_1^s}, \dfrac{\partial (L_1+L_2)}{\partial Y_2^s}]\) (Reduce-scatter)
对于 \(\bar{g}\) 我们有:
- 前向:\([W_1^s,W_2^s] = [(W_1+W_2)_{s_{a}}, (W_1+W_2)_{s_{b}}]\) (reduce-scatter)
- 反向:\(\dfrac{\partial L_1}{\partial W_1}=\dfrac{L_1}{\partial(W_1+W_2)}=[\dfrac{\partial L_1}{\partial W_1^s}, \dfrac{\partial L_1}{\partial W_2^s}]\),
- \(\dfrac{\partial L_2}{\partial W_2}=\dfrac{L_2}{\partial(W_1+W_2)}=[\dfrac{\partial L_2}{\partial W_1^s}, \dfrac{\partial L_1}{\partial W_2^s}]\) (all-gather)









 浙公网安备 33010602011771号
浙公网安备 33010602011771号