Megatron-LM Efficient AI training system
Efficient Large-Scale Language Model Training on GPU Clusters Using Megatron-LM
目录
摘要
- 模型训练的有效性收到了限制：
- GPU内存容量受限，模型很大无法容纳。
- 简单地使用向量/流水线秉性导致可扩展性不足。
- 展示了如何将向量，流水线和数据并行策略应用到千卡上。
- 提出了新型的交替流水线策略，可以提升：
- 吞吐率提升10%。
- 52%的理论极限吞吐率。
引入/背景
训练中遇到的困难（动机，先前方法的缺憾）
-
训练大模型遇到了以下的困难：
- 不可能将一个模型的所有参数都存入到单个GPU的内存中（甚至目前内存最大的A100，80GB）都不可能。
- 即使我们的模型足够小，训练也会需要很长时间（175B GPT-3 在V100上单卡训练时间约为288年。）
-
引入并行策略来减少运算时间。
- 数据并行的可扩展性很好，但有以下的两个挑战：
- 在超过一个限度后，每个GPU的批量很小，减少了GPU的利用率，并且增加了通信损耗。
- batch_size限制了使用的设备的数量。
- 张量并行策略将每个transformer内的矩阵运算分裂到多个GPU上，用于解决上述的两个不足。在20B大小的模型上运行看起来良好，但是在更大型的模型上表现不佳，主要为以下的两个新的问题：
- all-reduce通信在张量并行中需要通过服务器间的链路，这样将会比服务器内多卡间的高带宽NVLINK慢很多。
- 大量的模型并行将会创造出小型的矩阵乘法（GEMM）从而降低GPU运用率。
- 流水线并行也是一个用于解决大模型训练的技术。
- （1）模型的不同层将会分割到多个GPU上。
- （2）单个batch将会分成更小的microbatch，在这些microbatch上的执行将会形成流水线。
- 不同层的分配和调度策略将会导致不同的表现权衡。
- 除了调度外，为了满足全局的优化语义，优化器的step（更新模型参数）将需要在各个设备之间同步，导致在每个batch后的流水线刷新，使得microbatch完成执行（同时没有microbatch注入）。因此，为了达到更高的效率，提出了新的流水线调度来提升小批量数据的效率。
- 数据并行的可扩展性很好，但有以下的两个挑战：
主要关注点
- 文章主要关注：如何将并行策略结合在一起，最大化训练大模型过程中，给定batch大小的吞吐率，并且保持严格的优化语义。
- 文章展示了如何将流水线并行（跨服务器），张量并行（服务器内）和数据并行结合在一起达到良好的计算表现。
- 达到目的需要创新和严谨的工程，体现在以下几个方面：
- 核kernel的部署需要允许大部分计算是计算受限而非内存受限（最大化利用率）
- 计算图的分割要减少跨节点之间网络链路的传输，并且减少设备空闲的时间，优化域之间的通信。
- 以及充分使用硬件的特性。
主要工作
-
文航充分学习了各个部分是如何影响吞吐率的，提出了以下的配置分布式训练的原则：
- 不同形式的并行策略将会有多个方式的结合。并行策略的结合方式不佳时，将会降低吞吐率。
- 并行策略将会对通信数量造成影响。
- 核执行部署方式对计算效率带来的影响。
- 流水线刷新（气泡）过程中空闲工作节点的影响。
- 流水线并行策略的调度方式将会影响到通信的数量，流水线气泡的大小，以及用于储存激活的内存。
- 提出了一个新的交互调度将会提升10%左右的吞吐率。
- 超参数的值如microbatch的大小将会对内存占用，核计算的运算效率，以及流水线气泡大小。
- 在规模上，分布式训练对通信要求较高。因此节点间通信的缓慢或分割方式对通信的要求将会影响扩展效应。
- 不同形式的并行策略将会有多个方式的结合。并行策略的结合方式不佳时，将会降低吞吐率。
-
文章并没有自动化地探索并行策略的搜索空间来寻找较优策略，而是通过启发式方式来寻找。
并行策略的不同模式
数据并行[1]
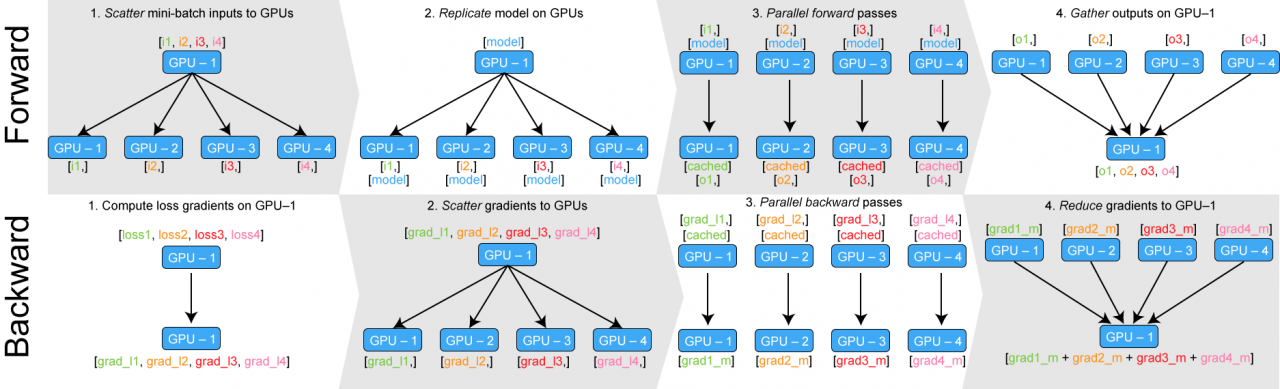
流水线并行
- 模型的不同层将会被切分到多个设备上。当使用具有相同重复的transformer块模型时，每个设备上将会被分配相同数量的transformer层。
- 本文不考虑不对称模型。
- 一个batch将会被切分成多个microbatch，这样流水线将会在microbatches中形成。
- 流水线方法需要保证输入在前向和反向传播时模型的权重不变，这样才能满足模型的同步更新语义。特别地，简单的流水线会导致模型输入在反向传播时遇到前向传播时没有发生的参数更新。
- 为了保证严格的优化器语义，我们引入了流水线的刷新策略。这里可以理解成barrier一样的语义。在每个batch的开始和结束，设备将会空闲。我们将空闲称为流水线气泡，目标是减少他们。有些工作采用异步操作或受限延迟的方式来避免流水线刷新操作，但这样将会放宽权重更新语义。这些不在这篇工作的考虑范围内。
- 有多种方式来调度前向和反向传播。每种方法将带来在气泡大小，通信，内存占用的不同权衡。主要讨论常规调度和交织调度模式。
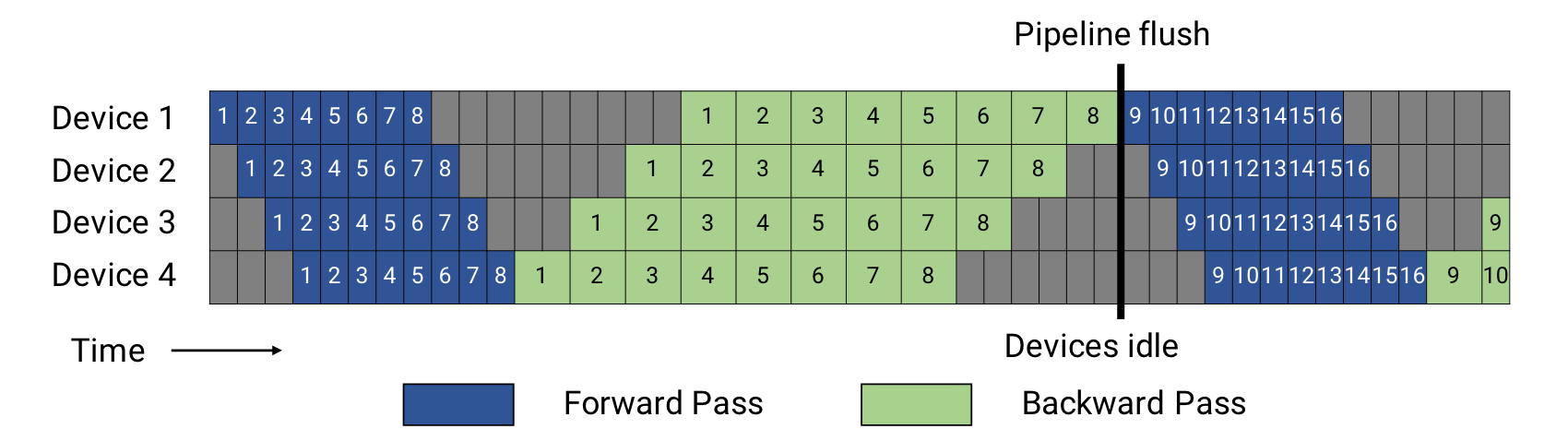
- 常规调度模式。
- 我们设microbatch的大小为\(m\)，\(p\)为流水线层数（也就是设备的数量），\(t_{id}\)为理论极限最优单batch时间。\(t_f\)为前向传播时间，\(t_b\)为反向传播时间。
- 从图中可以看到，前向传播需要等待microbatch自上而下传递到D4,因此出现了 \((p-1)\cdot t_f\) 的前向传播气泡时间。为了让梯度反向传播回设备1，我们需要 \((p-1)\cdot t_b\) 的反向传播时间。因此整个气泡时间就是 \((p-1)(t_f+t_b)\).
- 由此我们可以得到气泡时间占比：
\(t_{pb}/t_{id}=(p-1)(t_f+t_b)/m(t_f+t_b)=(p-1)/m\). - 减少占比的其中一个方式就是增加microbatch的数量，但是这会导致迭代时间过长并且内存占用大，因为我们需要储存许多中间运算产生的梯度和激活。
- 为了达到增加microbatch数量并且减少运算过程中产生的中间激活（梯度），我们采用PipeDream刷新调度。
- 这种调度限制了位于设备内的microbatch的数量（除了反向传播和正向激活过程中时间开销很大的必须保存以外）最多只能为流水线的层级数，并且在稳定后执行1F1B方式。这样虽然气泡是相同的，但是正在进行的前向、反向传播最多为流水线层数。这样，我们最多只需要储存 \(p\) 个中间结果，就可以实现 \(m>>p\).
- 阶段交替调度模式。
- 降低流水线气泡的形式，我们可以让每个设备进行多个层子集的运算（也称为模型块），而不是单个连续的层。
- 重新映射：假设我们有16层。原先的映射方式是 \(\{\{1,2,3,4\},\{5,6,7,8\},\{9,10,11,12\},\{13,14,15,16\}\}\), 现在变成了 \(\{\{1,2,9,10\},\{3,4,11,12\},\{5,6,13,14\},\{7,8,15,16\}\}\)。这样就相当于模型被分成了两块（每个microbatch需要经过的设备次数）。
- 这样原先的前向和反向传播时间（可以看做是流水线的两个时钟周期）将从 \(t_f\to t_f/v\), \(t_b\to t_b/v\). \(v\) 为模型的块数。原先的气泡时间就变成了 \((p-1)(t_f+t_b)/v\).
- 整体的理想时间仍然为\((t_f+t_b)m\). 这样气泡占比将会下降成：\(1/v\cdot (p-1)/m\).
- 但是这样将会引入通信的开销，通信开销将增加到原先的 \(v\) 倍。
张量并行[2]
-
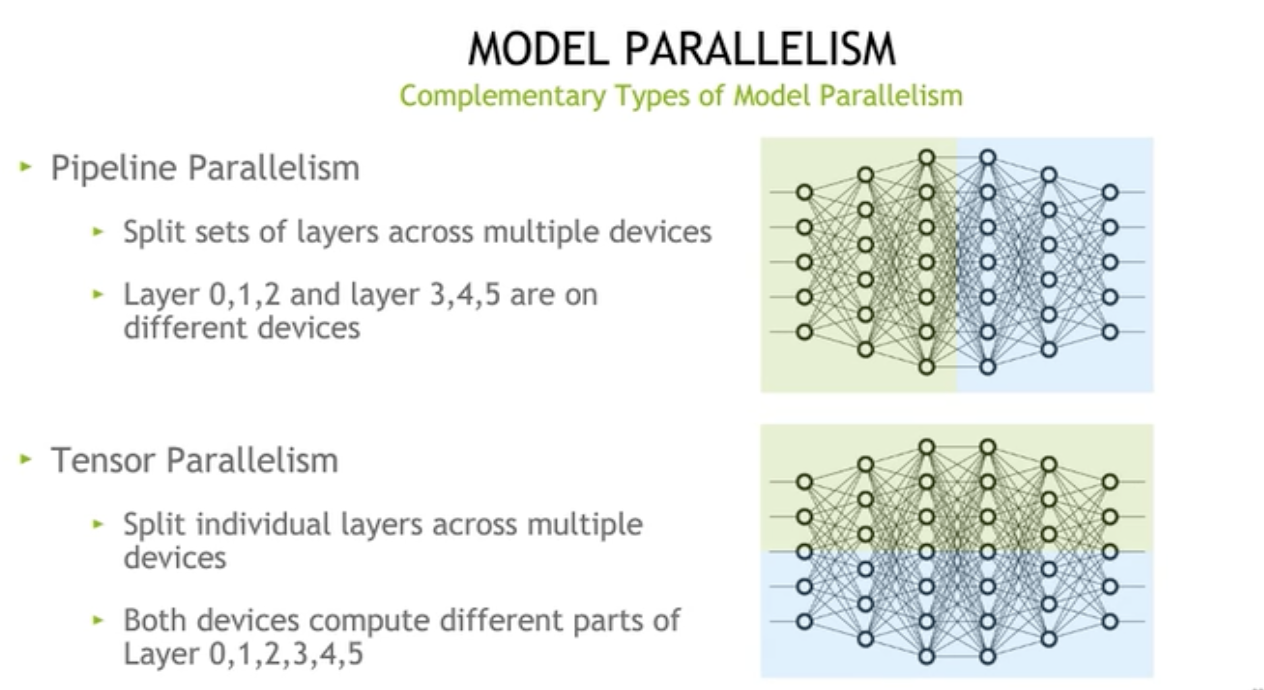
流水线并行
- 将模型层的子集分配到不同的设备上。
- 层0,1,2和层3,4,5在不同的设备上。分割的维度垂直于数据流。
-
张量并行
- 将单个层分割到不同的设备上。
- 这样层0,1,2,3,4,5均有两部分分别位于设备0和1上。
-
张量并行方式：行并行和列并行
- 行并行
![img]()
- 列并行
![img]()
-
接下来介绍有关MLP的张量并行方法。[3]
-
行并行策略如下：
![img]()
-
在行并行策略中，我们的 \(X\) 和 \(A\) 都将会分离。这样我们在 \(f\) 处有：
\[\begin{aligned}
f:\begin{cases}
\text{forward(split):} &X = [X_1 ~~~~ X_2]\\
\text{backward(merge):}&\dfrac{\partial L}{\partial X} = \left[\dfrac{\partial L}{\partial X_1} ~~~~ \dfrac{\partial L}{\partial X_2}\right]\text{(all-gather)}
\end{cases}
\end{aligned}
\]
- 同样在 \(g\) 处有：
\[\begin{aligned}
g:\begin{cases}
\text{forward(sum):} &Y = Y_1+Y_2~~\text{(all-reduce)}\\
\text{backward:}&\dfrac{\partial L}{\partial Y} = \dfrac{\partial L}{\partial Y_i}~~\text{(identity)}
\end{cases}
\end{aligned}
\]
- 我们在 \(f\) 的反向传播处和 \(g\) 的前向传播处采用了两种通信方式：all-reduce 与 all-gather.[4]
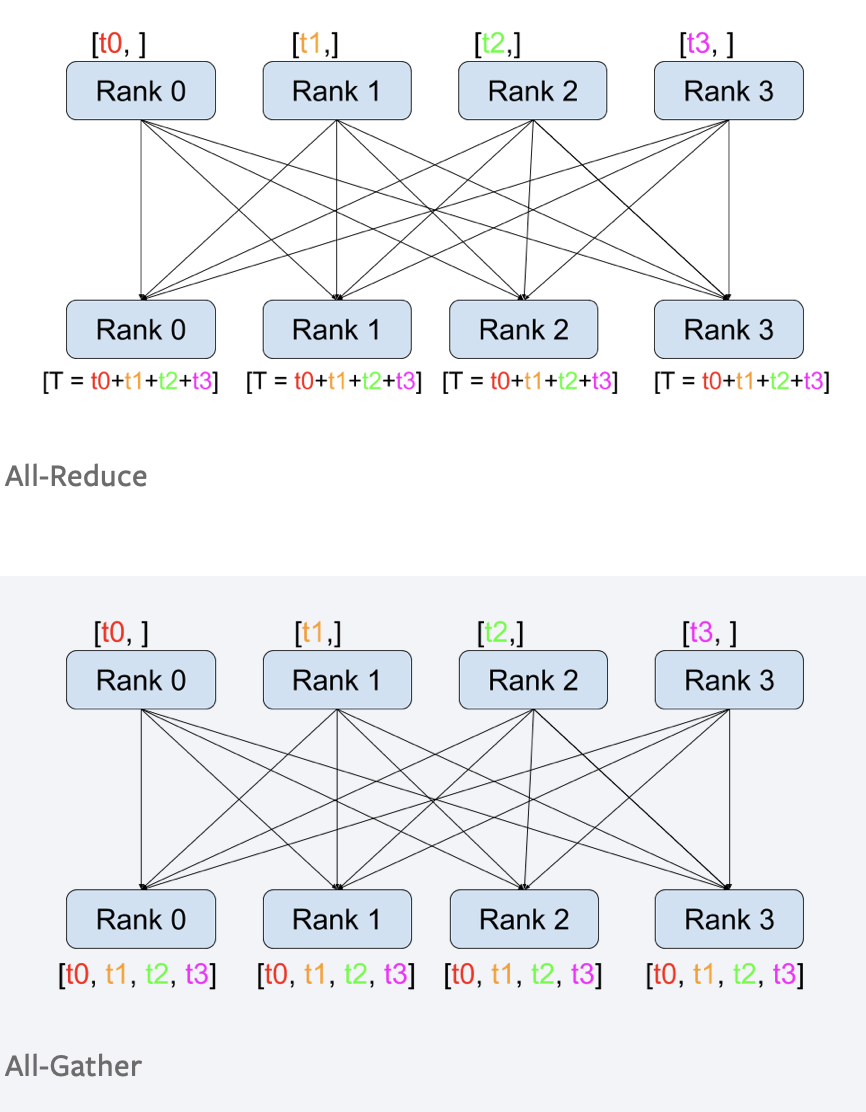
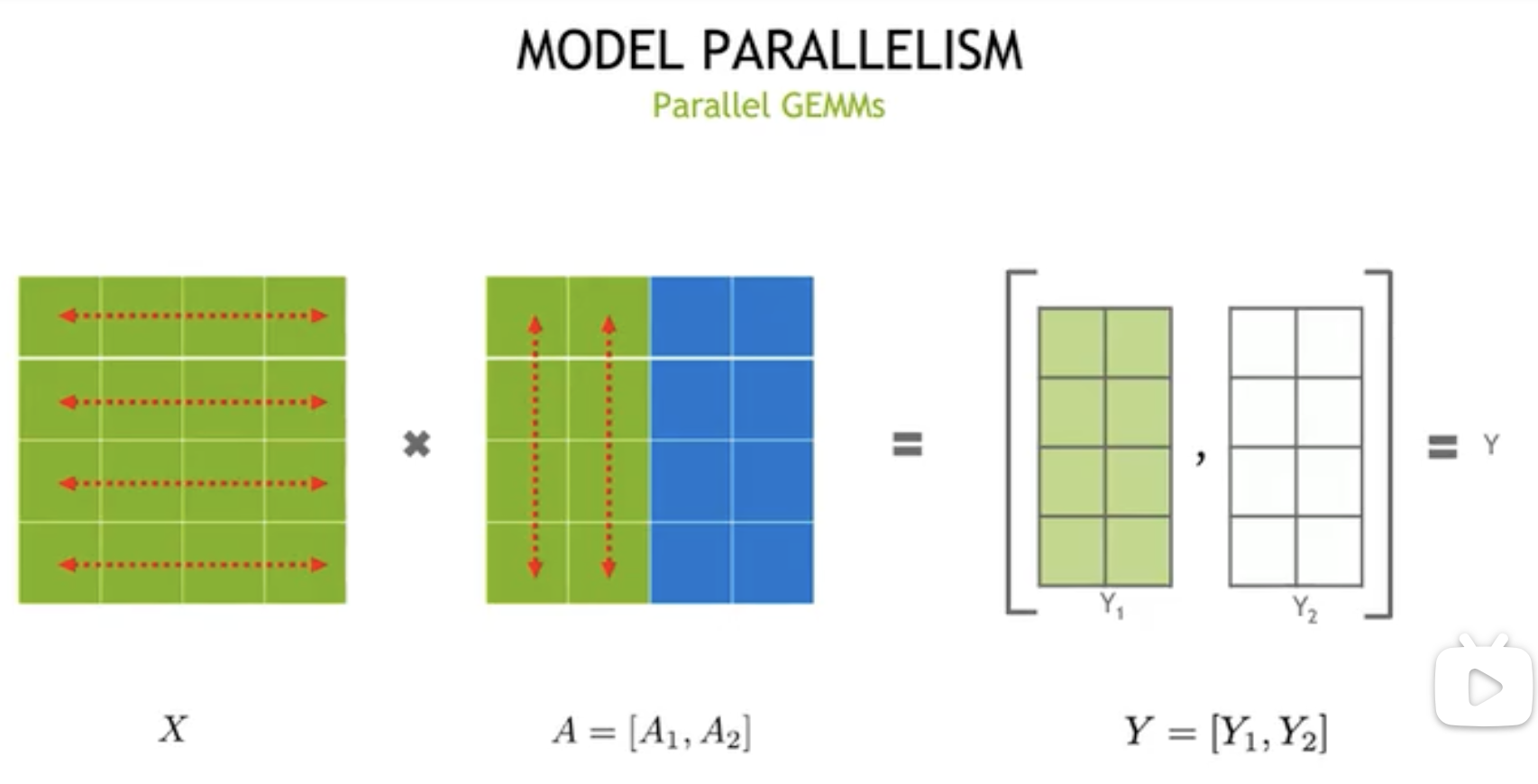
- 对于列并行策略，我们不对 \(X\) 进行切分，仅对 \(A\) 权重进行切分。这样我们有：
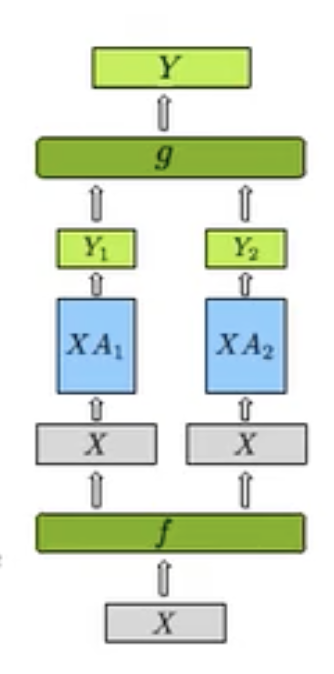
这样我们在 \(f\) 处有：
\[\begin{aligned}
f:\begin{cases}
\text{forward(identity):} &X = X\\
\text{backward(merge):}&\dfrac{\partial L}{\partial X} = \dfrac{\partial L}{\partial X}|_{\text{1}} + \dfrac{\partial L}{\partial X_2}|_{\text{2}}\text{(all-reduce)}
\end{cases}
\end{aligned}
\]
- 同样在 \(g\) 处有：
\[\begin{aligned}
g:\begin{cases}
\text{forward(sum):} &Y = [Y_1~~~~Y_2]~~\text{(all-gather)}\\
\text{backward:}&\dfrac{\partial L}{\partial Y} = \dfrac{\partial L}{\partial Y_i}~~\text{(split)}
\end{cases}
\end{aligned}
\]
对于transformer，内部含有的MLP块中，我们具有 \(GELU(x)\) 非线性激活函数，这也就意味着对 \(Y\) 进行的 all-reduce操作将会改变原先的语义，因为 \(GeLU(Y_1+Y_2)\neq GeLU(Y_1)+GeLU(Y_2)\)。
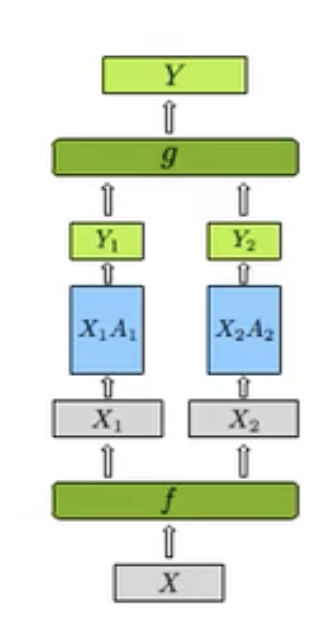
在MLP块中，我们对权重矩阵A进行列分割（GELU前），对权重矩阵B进行行分割（GELU）后，如图中所示：
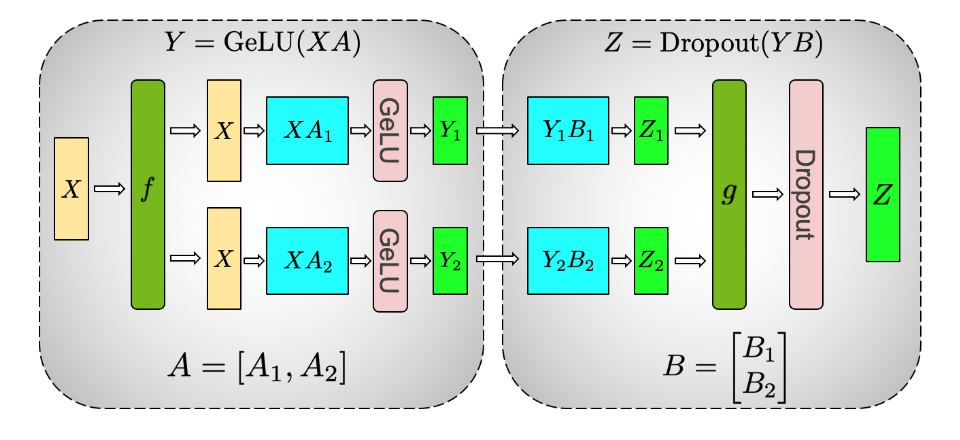
这样我们就有：X经过f不分割，前向进行identity操作，反向进行all-reduce操作。
\[\begin{aligned}
f:\begin{cases}
\text{forward(identity):} &X = X\\
\text{backward(merge):}&\dfrac{\partial L}{\partial X} = \dfrac{\partial L}{\partial X}|_{\text{1}} + \dfrac{\partial L}{\partial X_2}|_{\text{2}}\text{(all-reduce)}
\end{cases}
\end{aligned}
\]
经过中间激活层。
\[\begin{aligned}
Y &= [GeLU(XA_1) ~~~~ GeLU(XA_2)]\\
B &= \begin{bmatrix}
B_1\\B_2
\end{bmatrix}
\end{aligned}
\]
这样在 \(g\) 处进行的操作正好与 \(f\) 相互对偶。前向进行all-reduce操作，反向进行identity操作。
\[\begin{aligned}
g:\begin{cases}
\text{forward(sum):} &Z = Z_1+Z_2 ~~\text{(all-reduce)}\\
\text{backward:}&\dfrac{\partial L}{\partial Y} = \dfrac{\partial L}{\partial Y_i}~~\text{(identity)}
\end{cases}
\end{aligned}
\]
对于一个transformer的attention模块，我们的缩放点积操作仍然具有非线性层 softmax. 因此我们也无法使用行并行策略。仍然采用列并行策略，我们有：
我们将X分成两份注意力头：（Q，K，V均有两份）。剩余的部分仍然和MLP是相似的。这里就无需赘述了。仍然是f反向和g前向，总共两次all-reduce操作。这样每一个自注意力模块就需要四次all-reduce通信。
并行策略的结合与讨论
从本节开始，文章开始详细讨论不同并行策略结合在一起对内存占用，设备利用率和通信数据量之间的相互讨论。
记号表示
- \(n\) 表示GPU的数量，我们用三元组 \((p,t,d)\)分别代表：流水线并行的数量，张量并行的数量，数据并行的数量。
- \(B\)为全局batch的大小。\(b\)为microbatch的大小。
- \(m\) 代表每个流水线中具有的microbatch数量。
- 为什么？根据上面我们举一个进行2张量并行，4流水线并行，2数据并行，总共有16层的例子。采用1F1B流水线形式，我们有：
- 我们有 \((p,t,d)=(4,2,2)\), 因此需要16个GPU设备。
- 假设全局的batch大小为 \(B\)， 这样我们需要按照 \(p\) 分成microbatch，再按照 \(d\) 用于DP（数据并行）。（Q: 为什么没有 \(t\)? A: 因为张量并行按照列分割，不需要分裂输入数据。）这样每条流水线内具有 \(m=\frac{B}{pb}\).
仅存在张量并行和流水线并行情况分析
- 根据前面的分析我们知道，对于理想的数据处理时间为 \(t_{id}=m(t_f+t_b)\). 对于我们的流水线气泡，我们有 \(t_p=(p-1)(t_f+t_b)/v\), 这里文章仅考虑了 chunk=1 的情况。那么气泡大小占比（我们可以看做是1-占空比）为：
\[\dfrac{t_p}{t_{id}}=\dfrac{p-1}{m}=\dfrac{\dfrac{n}{t}-1}{m}
\]
此处的 \(d=1\)，因此 \(n = pt\).
- 接下来考虑通信数据量大小。我们设一个microbatch的大小为 \(bsh\), 其中 \(s\) 为序列长度，\(h\) 为隐藏层维度。
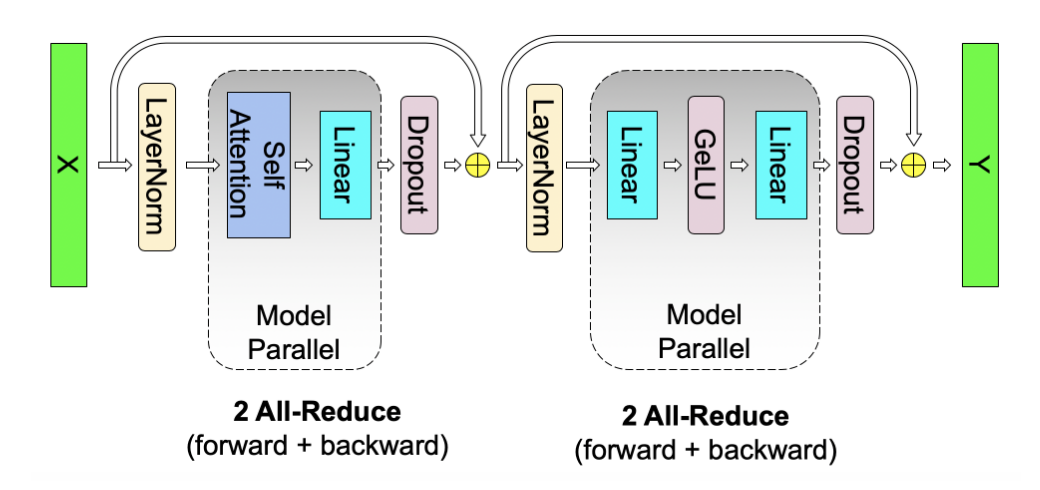
- 对于每次的transformer block，我们要经过一个自注意力层和一个MLP+GELU层。根据下图和上面的分析，我们需要2次 \(f\) 反向all-reduce， 两次 \(g\) 前向all-reduce。
- 接下来需要了解all-reduce的通讯量。在NVIDIA的NCCL通讯库中，我们可以了解到，all-reduce算法采用的是ring all-reduce。主要的流程如下。
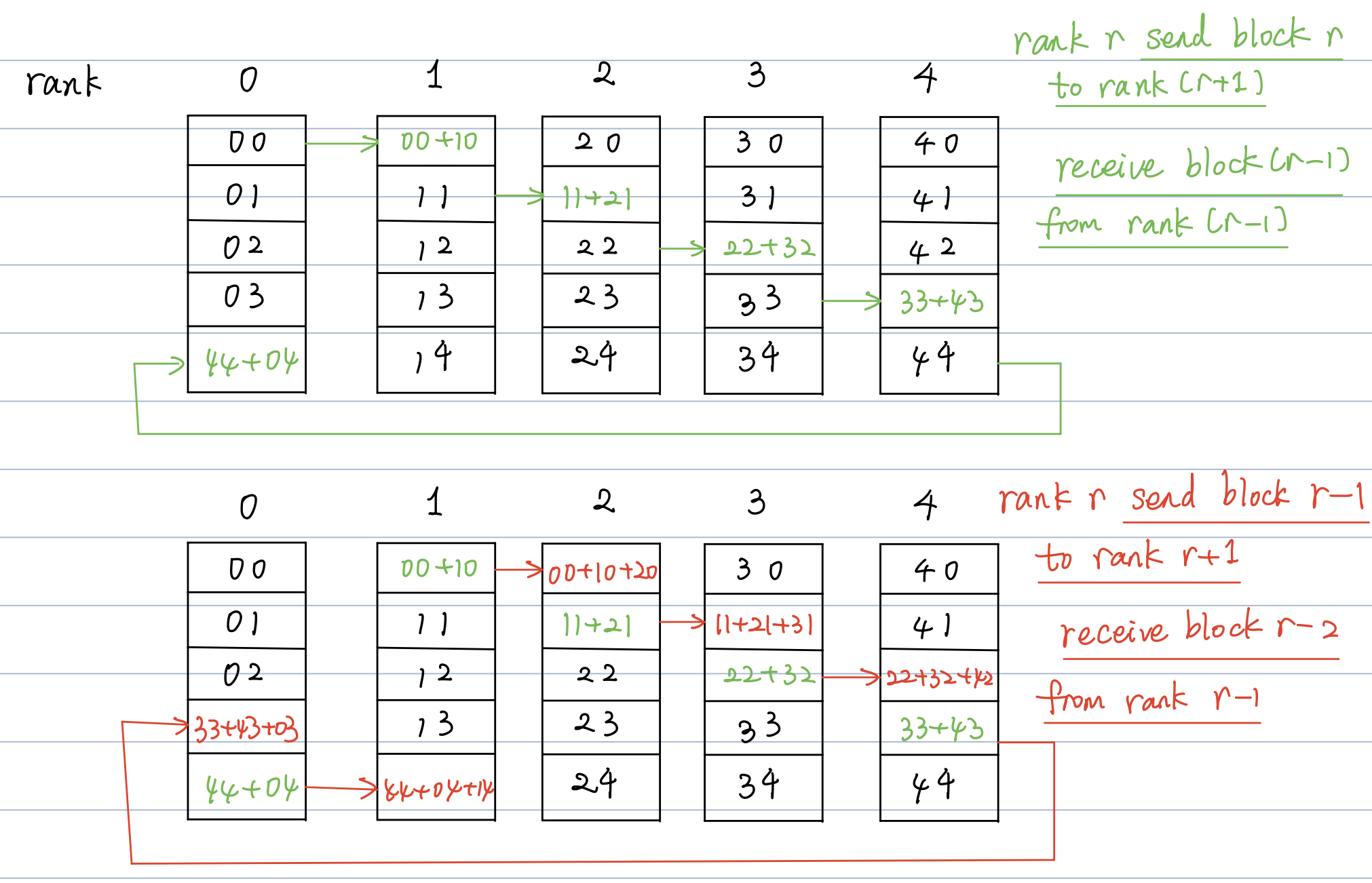
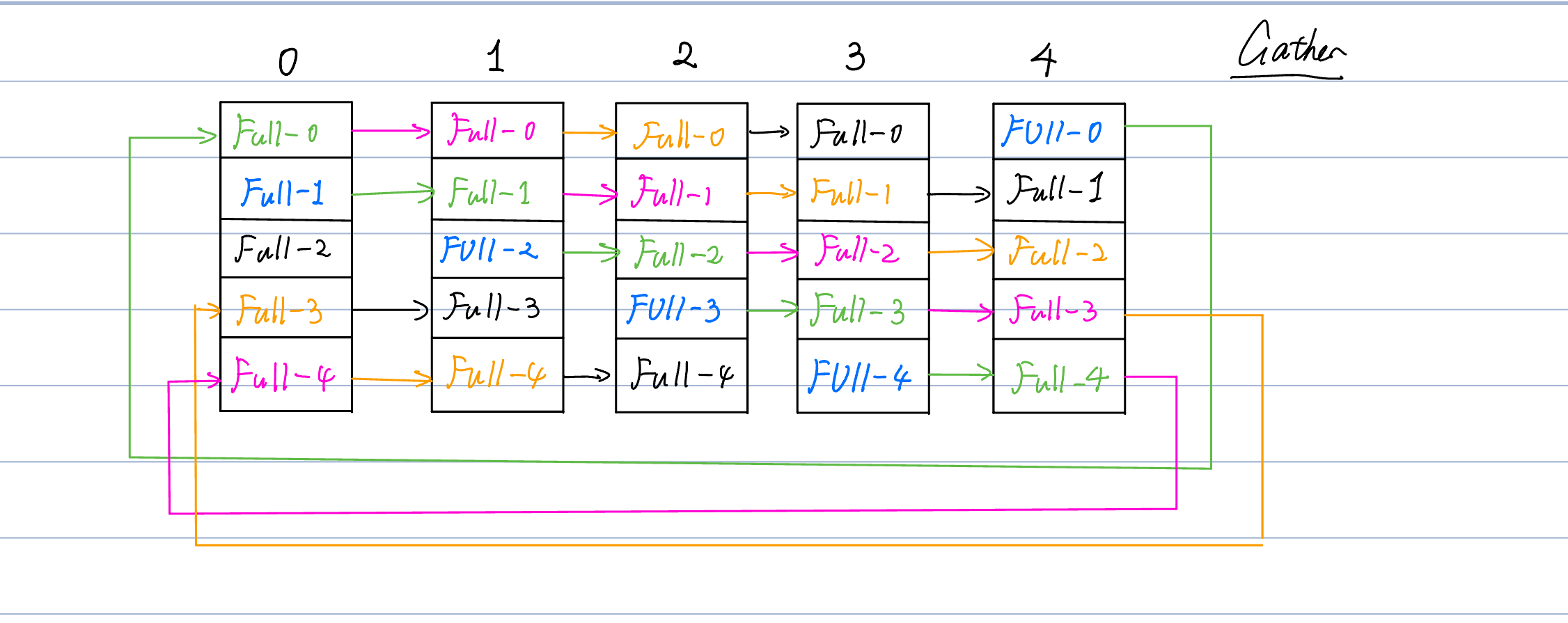
- 将数据分割成 \(t\) 块。
- 每个时刻，第 \(i\) 个设备将 \(((i-1)+t)\mod t\) 块数据传递给第 \((i+1)\mod t\)号设备。
- 每次传递的数据量即为 \(bsh/t\), 经过 \((t-1)\) 时间后，第 \(i\) 号设备将获得 \((i+1)\mod t\) 上数据的完整求和信息。
- 接下来将对应块的信息再传递给所有的设备。再经过 \((t-1)\) 时刻传递后，信息传递完成。
- 因此，经过4次all-reduce操作总共耗时 \(2(t-1)\)，通信量为 \(4\times 2\times\left(\dfrac{t-1}{t}\right)bsh=8\left(\dfrac{t-1}{t}\right)bsh\)
- 这样，假设在流水线中有 \(l^{stage}\) 个层级，我们就会出现通讯量 \(8\cdot l^{stage}\left(\dfrac{t-1}{t}\right)bsh\).
- 这样，当 \(t\) 大于一个工作节点（机器）内的GPU数量的时候，节点间缓慢链路的通信将会使得模型并行不太实用。因此我们有：
经验1:张量并行的度数应设置为g，当使用g-GPU的服务器时。这样我们能对跨服务器的更大模型应用流水线并行。
数据并行与其他模型并行结合
这一节主要讨论了数据并行分别与张量并行和流水线并行结合时的情况。为了简化，并没有将三者混在一起进行分析。
DP+PP
- \(t=1\).
- 每一级流水线将会接收到的microbatch的数目：\(m=B/(d\cdot b)\). 我们令 \(B/b=b'\)。\(b\) 为microbatch的大小， \(d\) 是数据并行的维度。
- 对于 \(n\) 个设备，我们的流水线层级为 \(p=n/(t\cdot d)\). 这样，我们具有以下的流水线气泡大小：
\[\dfrac{p-1}{m}=\dfrac{n/d - 1}{b'/d}=\dfrac{n-d}{b'}
\]
- 这样，随着 \(d\) 不断增大，气泡时间将不断变小。并且，由于单个设备内存过小，\(d\) 也很难达到 \(n\)。
- 根据先前的分析也可以得到，我们的all-reduce操作在基于ring的方式下需要的执行时间为 \((d-1)/d\).
- 我们也可以分析全局batchsize的作用。对于一个给定的配置，当batch_size大小增加时，\(b'=B/b\) 也会增加，这样流水线气泡时间也会同步变小。这样DP所需要进行的all-reduce操作频率也会增加，提升模型的吞吐率。
DP+TP
- 进行TP的过程中，all-reduce会在每一个microbatch中进行。也就是DP间需要all-reduce，同时前向和反向的 \(g\) 和 \(f\) 也需要各进行两次all-reduce。这样在跨多GPU服务器间将开销很大。
- 对于某些不太大的层，进行TP后可能会导致GPU无法完全利用（达不到计算峰值）。
经验2：采用DP和模型并行时，总体的模型并行大小 \(M=t\cdot p\) 应该调整到模型的参数和中间元数据能够适配GPU内存。DP可以扩展到更多GPU上。
Microbatch的大小
- 对于microbatch大小的选择也会影响到模型训练的吞吐率。
- 对于一个配置 \((p,t,d)\), 以及一个全局的batch大小 \(B\)，我们有完成一个batch所需要的时间（这里没有考虑通信时间）：
- 流水线气泡时间 \((p-1)(t_f(b)+t_b(b))\)
- 流水线理想时间 \(m(t_f(b)+t_b(b))\)
- 流水线中microbatch的数量: \(B/(b\cdot d)=b'/b\)
- 因此整体的开销时间为
\[(b'/b+p-1)\cdot(t_f(b)+t_b(b))
\]
- 因此microbatch的大小 \(b\) 将会对运算强度和流水线气泡大小均造成影响。
经验3：最优的microbatch大小取决于吞吐和模型的内存占用特性，以及\((p,d,B)\).（感觉是废话）
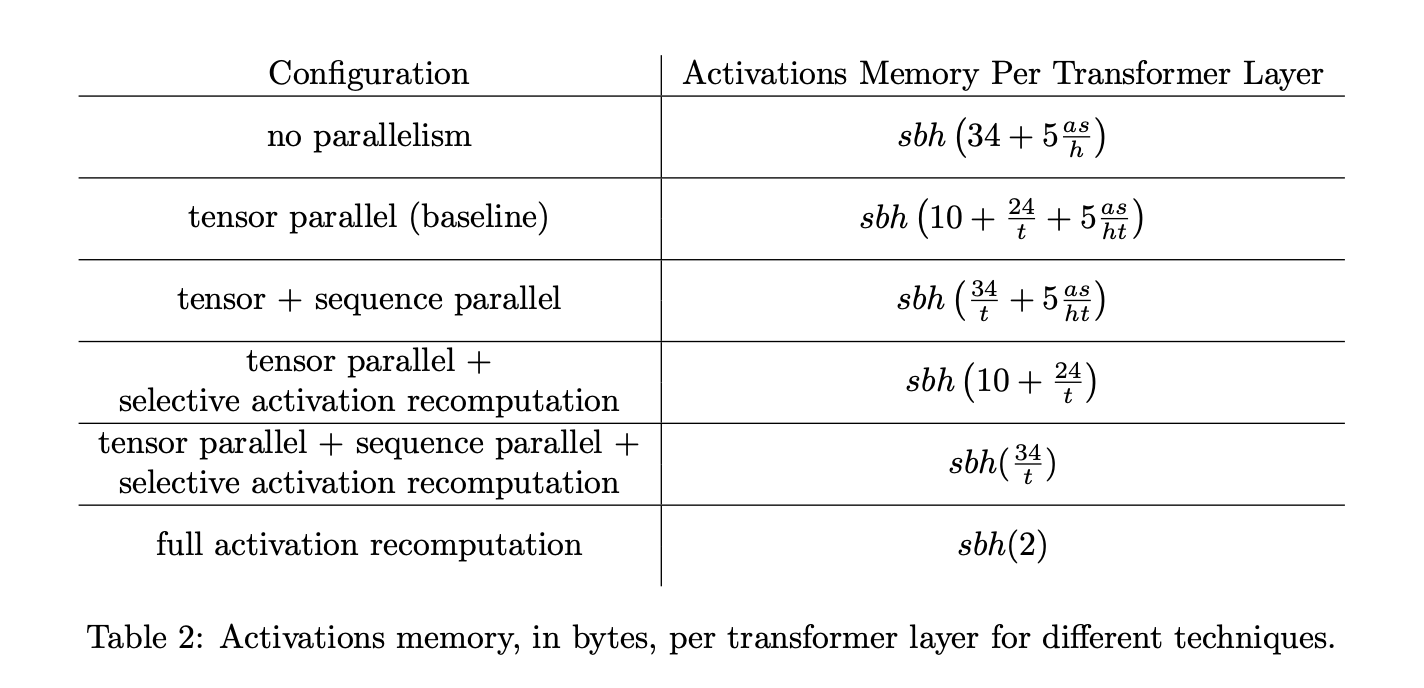
激活重计算
- 如文章所说，激活冲运算是一个可选择的技巧，用于实现权衡计算复杂度和内存占用的技术。这项技术在flash-attention中也有所使用，目的是为了减少对HBM的读取，将通信时间减少。（通信时间为瓶颈）。
- 通过在反向传播前再进行一次前向传播，仅仅储存流水线并行过程中计算好的激励，而不是将所有的中间激励都储存）。
- 激励储存点不会影响吞吐率，但是影响内存占用。
- \(A_1\):输入大小。
- \(A_2\):每一层的中间激励大小。
- \(l\): 一个模型的层数。
- \(c\): 检查点数目。
- 这样计算出来的总内存占用为
\[c\cdot A_1+\dfrac{l}{c}\cdot A_2
\]
很容易看出当 \(c=\sqrt{l\cdot(A_2/A_1)}\) 时得到最小的内存占用。
部署
采用pytorch进行部署，利用NCCL进行设备间通信。为了优化效果，我们实现了对通信和对计算的优化。
通信优化
我们可以看以下的图。
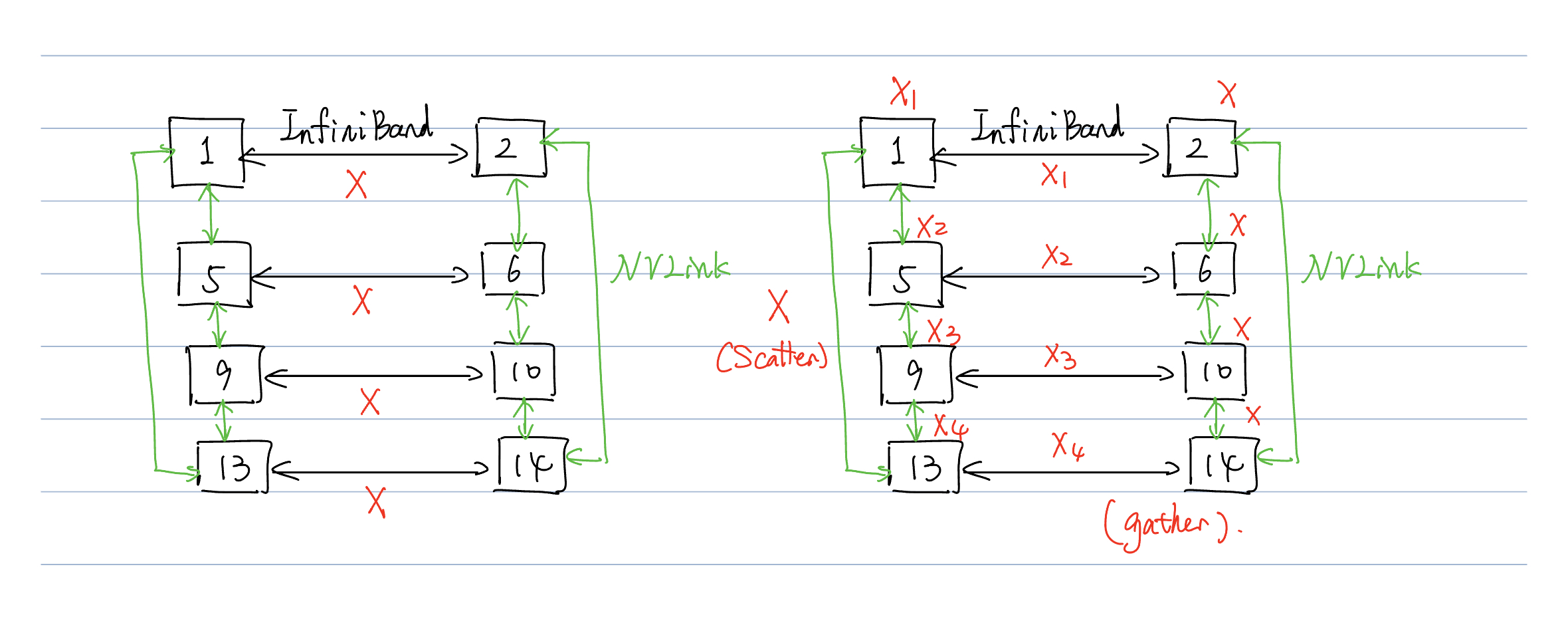
- 在其中，{1,5,9,13}位于工作节点1. {2,6,10,14}位于工作节点2.工作节点之间采用InfiniBand连接，工作节点内采用NVLINK连接。节点内通信速度要远快于节点间通信。
- 这样，我们前面采取的列分割模型并行的方式将会每次在工作节点间传递整一个X，这样会导致无法达到最优的通信情况。
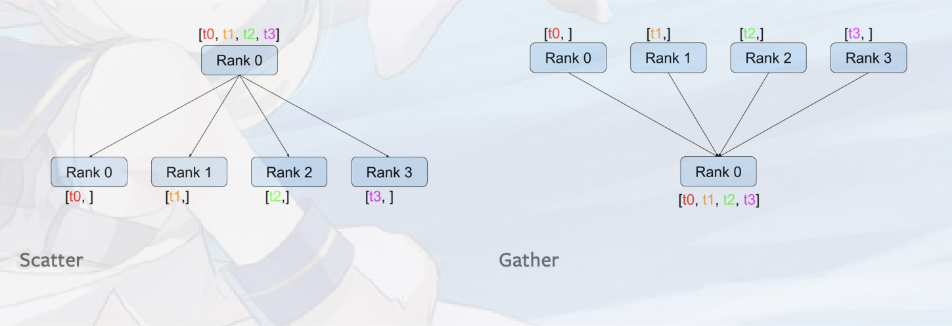
- 于是，我们将X分裂成四个chunk \([X1, X2, X3, X4]\)。这样，在进行传输前，首先调用scatter源语将其分裂成四块。
- 然后每个IB链路将仅仅传递一个chunk。这样传递到下一级流水线后再使用gather源语即可。
- 这样跨节点传输大小将从原先的 \(bsh\) 下降到 \(bsh/t\)。
运算优化
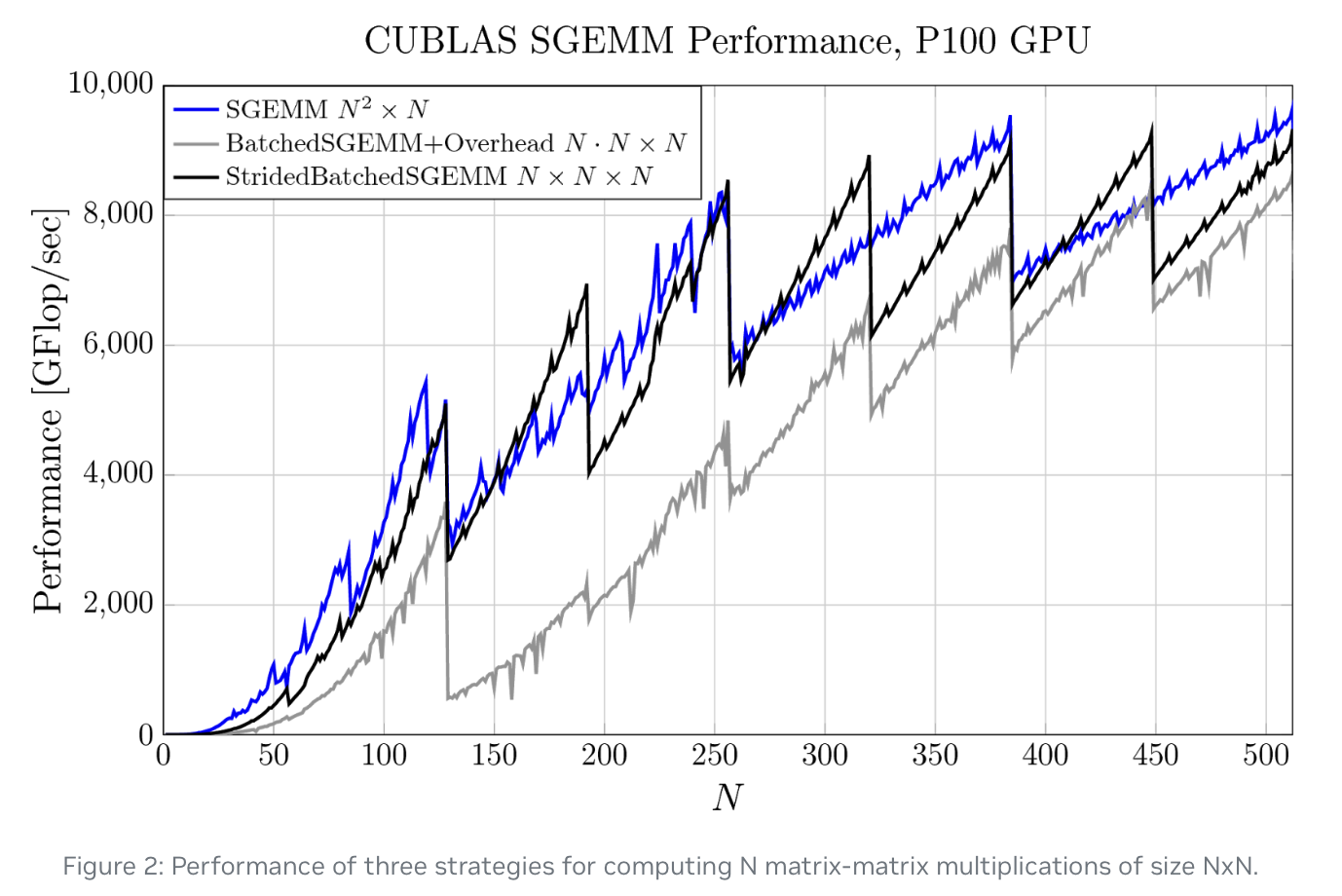
- 改变数据的布局来避免出现内存紧张的矩阵转置操作，并且采用strided batch gemm[6]来尽可能的提升计算速度。
- 将数据从 \([b,s,a,h]\) 的batch_first布局改变成了 \([s,b,a,h]\)
- 采用pytorch 即时编译(JIT)来针对逐元素运算的一系列操作融合成一个核。
- 生成了两个自定义的运算核进行缩放，掩码和softmax操作：一个用于普通的掩码（例如BERT类型模型）操作，一个用于因果掩码操作（例如GPT类型模型）。
浙公网安备 33010602011771号