SkipList

SkipList

经典的数据结构。这里我们借用CMU15445 2025 Spring的仓库来实现我们的跳表结构。相关的论文可以查看：
Skip Lists: A Probabilistic Alternative to Balanced Trees

目录

• SkipList
  • 头文件定义
  • 跳表ADS描述
    • 初始化
    • 搜索
    • 插入操作
      • 生成节点高度
    • 删除操作
  • 时空复杂度分析
    • 时间复杂度分析
    • 空间复杂度
  • 应用

头文件定义

#pragma once
#include <cstddef>
#include <cstdint>
#include <functional>
#include <memory>
#include <random>
#include <shared_mutex>
#include <vector>
#include "common/macros.h"
namespace bustub {
// 采用宏定义来简化模版。
#define SKIPLIST_TEMPLATE_ARGUMENTS template <typename K, typename Compare, size_t MaxHeight, uint32_t Seed>
template <typename K, typename Compare = std::less<K>, size_t MaxHeight = 14, uint32_t Seed = 15445>
// 定义一个跳表结构体，里面具有多个节点。
class SkipList {
 protected:
  struct SkipNode;

 public:
  // 显式构造函数，将表头初始化成一个具有最高高度的节点。所有的节点都指向NULL。
  explicit SkipList(const Compare &compare = Compare{}) { 
    compare_ = compare;
    header_ = std::make_shared<SkipNode>(MaxHeight);
  }
  // 析构函数。
  ~SkipList() { Drop(); }

  // 删除了拷贝构造函数和移动构造函数，并且禁止了拷贝赋值和移动赋值。
  SkipList(const SkipList &) = delete;
  auto operator=(const SkipList &) -> SkipList & = delete;
  SkipList(SkipList &&) = delete;
  auto operator=(SkipList &&) -> SkipList & = delete;
  
  // 一些经典的调表操作。
  auto Empty() -> bool;
  auto Size() -> size_t;
  void Clear();
  auto Insert(const K &key) -> bool;
  auto Erase(const K &key) -> bool;
  auto Contains(const K &key) -> bool;
  void Print();

 protected:
  auto Header() -> std::shared_ptr<SkipNode> { return header_; }

 private:
  // 随机生成高度。
  auto RandomHeight() -> size_t;
  void Drop();  // 按照顺序删除整个跳表。
  static constexpr size_t LOWEST_LEVEL = 0;
  Compare compare_;
  std::shared_ptr<SkipNode> header_;
  uint32_t height_{1};
  size_t size_{0};
  std::mt19937 rng_{Seed};
  std::shared_mutex rwlock_{};  // 读写锁。
};

// 跳表节点的定义。
SKIPLIST_TEMPLATE_ARGUMENTS struct SkipList<K, Compare, MaxHeight, Seed>::SkipNode {
  explicit SkipNode(size_t height, K key = K{}) {
    links_ = std::vector<std::shared_ptr<SkipNode>>(height, std::shared_ptr<SkipNode>());
    key_ = key;
  }

  auto Height() const -> size_t;
  auto Next(size_t level) const -> std::shared_ptr<SkipNode>;
  void SetNext(size_t level, const std::shared_ptr<SkipNode> &node);
  auto Key() const -> const K &;

  std::vector<std::shared_ptr<SkipNode>> links_;
  K key_;
};
}

跳表ADS描述

整个跳表可以用这样一张经典的图来概括：

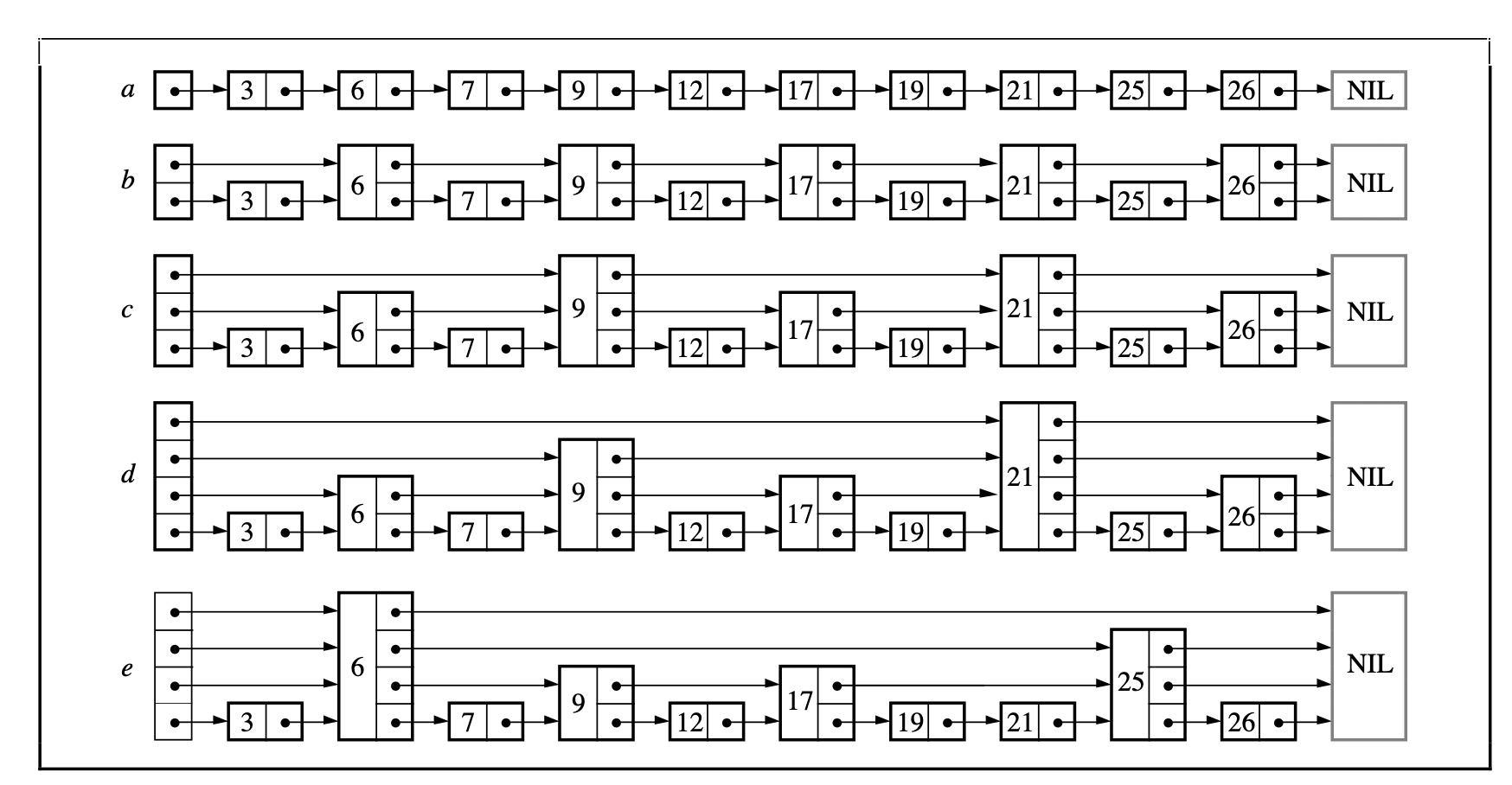
初始化

我们首先需要对跳表进行初始化，规定头结点的最高高度后（采用模板参数定义为14），生成头结点。这样我们就有构造函数，生成跳表的比较规则（跳表内部是有序的），：

explicit SkipList(const Compare &compare = Compare{}) { 
    compare_ = compare;
    header_ = std::make_shared<SkipNode>(MaxHeight);
}
explicit SkipNode(size_t height, K key = K{}) {
    links_ = std::vector<std::shared_ptr<SkipNode>>(height, std::shared_ptr<SkipNode>());
    key_ = key;
}

这样，我们在跳表数据结构中生成了头结点（是一个指向跳表节点的共享指针）。调用跳表节点的构造函数生成了一个高度为14，所有的节点都指向空节点的指针。

搜索

我们的搜索函数用于判断跳表中是否存在一个声称的节点。通过函数Contains进行。函数声明如下：

auto Contains(const K &key) -> bool;

在执行搜索的时候，我们需要自上而下地进行搜索。此处需要使用双指针的经典想法。我们定义两个指针cur和forward进行搜索。跳表内部的节点是具有顺序的，因此我们可以进行如下操作：

1. 当forward指针的值小于目标值时，我们继续将两个指针向前移动。
2. 当forward指针的值大于目标值的时候，我们将降低搜索高度，重新获取cur和forward指针，在新的高度进行搜索。
3. 直到高度为0时或者找到目标值为止。

SKIPLIST_TEMPLATE_ARGUMENTS auto SkipList<K, Compare, MaxHeight, Seed>::Contains(const K &key) -> bool {
  std::shared_lock lock(rwlock_);   // 读写锁。
  // 双指针进行搜索。
  std::shared_ptr<SkipNode> current_pointer = header_;
  std::shared_ptr<SkipNode> forward_pointer;
  // 自上而下依次搜索。
  for(size_t i = MaxHeight; static_cast<int>(i) >= 0; i--) {
    forward_pointer = current_pointer -> Next(i);
    // 在当前高度遍历直到寻找到对应值或者到达nullptr。
    while(forward_pointer != nullptr && compare_(forward_pointer -> Key(), key) == true) {
      current_pointer = forward_pointer;
      forward_pointer = forward_pointer -> Next(i);
    }
  }
  current_pointer = forward_pointer;
  if(current_pointer == nullptr) {
    return false;
  }
  return static_cast<bool>(compare_(key, current_pointer -> Key()) == false 
    && compare_(current_pointer -> Key(), key) == false);
}

插入操作

同样作为链表型数据结构，插入操作就避无可避。这样我们还是需要延用先前的搜索的想法，但相对应有区别的是，插入操作需要改变链表结构，因此添加前驱和后缀节点就需要我们在遍历过程中记录他们。这样我们就需要

1. 首先进行contains操作，判断节点是否存在。在contains操作中逐层记录我们需要的前驱和后缀节点信息。
2. 如果没有找到当前节点，我们则需要将节点插入到跳表当中，根据先前的操作寻找到我们需要的前驱和后缀信息，将前驱节点指向插入节点，插入节点的后缀指向后缀节点即可。

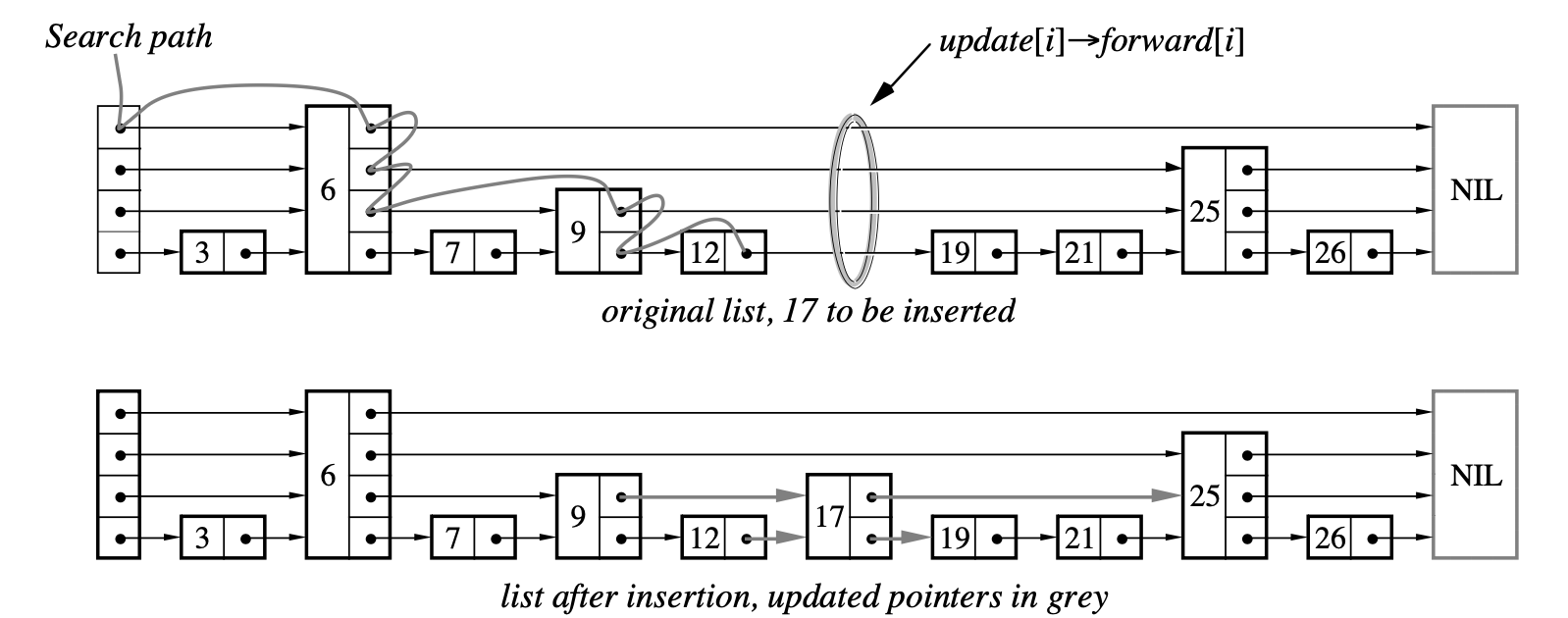
例如上述的图片，我们首先逐层遍历，这样我们的前驱节点自上而下记录为{6,6,9,12}，后缀节点记录为{NULL, 25, 25, 19}.这样我们就有：

auto Insert(const K &key) -> bool;

SKIPLIST_TEMPLATE_ARGUMENTS auto SkipList<K, Compare, MaxHeight, Seed>::Insert(const K &key) -> bool {
  std::unique_lock lock(rwlock_);

  // 分别记录前驱节点和后缀节点。
  std::vector<std::shared_ptr<SkipNode>> next_container;
  std::vector<std::shared_ptr<SkipNode>> cur_container;
  // 还是相同的双指针操作。
  std::shared_ptr<SkipNode> current_pointer = header_;
  std::shared_ptr<SkipNode> forward_pointer;

  for(size_t i = MaxHeight - 1; static_cast<int>(i) >= 0; i--) {
    forward_pointer = current_pointer -> Next(i);
    // 对每一层进行遍历。
    while(forward_pointer != nullptr && compare_(forward_pointer -> Key(), key) == true) {
      current_pointer = forward_pointer;
      forward_pointer = forward_pointer -> Next(i);
    }
    cur_container.push_back(current_pointer);
    next_container.push_back(forward_pointer);
  }
  // 寻找到已插入节点时停止操作。
  if (forward_pointer != nullptr &&
      compare_(forward_pointer->Key(), key) == false &&
      compare_(key, forward_pointer->Key()) == false) {
    return false;
  }
  // 随机生成节点的高度，并构造节点。
  size_t new_height = RandomHeight();
  std::shared_ptr<SkipNode> new_node = std::make_shared<SkipNode>(new_height, key);
  // 将节点的前驱和后继相互连接。注意我们的节点存储是自上而下的，因此这里也应该反过来取节点相互连接。
  for(size_t i = 0; i < new_height; i++) {
    std::shared_ptr<SkipNode> pre_node = cur_container[MaxHeight - 1 - i];
    std::shared_ptr<SkipNode> next_node = next_container[MaxHeight - 1 - i];
    pre_node -> SetNext(i, new_node);
    new_node -> SetNext(i, next_node);
  }
  size_++;
  height_ = height_ > new_height ? height_ : new_height;
  return true;
}

生成节点高度

跳表采用随机化的方式为新的节点生成高度，但这样的随机化也存在部分的规则。我们生成高度的方式如下：

1. 初始高度为1.
2. 生成随机数，随机数的范围在 \([0,1)\) 之间。
3. 当随机数小于规定的一个 \(p\) 值时，高度增加直到达到最高的高度。

我们可以采用几何分布的方式进行。这里将会有25%的概率上升高度，也就是 \(p=0.25\)。

SKIPLIST_TEMPLATE_ARGUMENTS auto SkipList<K, Compare, MaxHeight, Seed>::RandomHeight() -> size_t {
  // Branching factor (1 in 4 chance), see Pugh's paper.
  static constexpr unsigned int branching_factor = 4;
  // Start with the minimum height
  size_t height = 1;
  while (height < MaxHeight && (rng_() % branching_factor == 0)) {
    height++;
  }
  return height;
}

删除操作

也是和上面相同的原理。采用的是搜索+记录的方式进行。也需要同样记录前驱和后继节点。

auto Erase(const K &key) -> bool;

SKIPLIST_TEMPLATE_ARGUMENTS auto SkipList<K, Compare, MaxHeight, Seed>::Erase(const K &key) -> bool {
  std::unique_lock lock(rwlock_);
  // 记录前驱后继节点。
  std::vector<std::shared_ptr<SkipNode>> next_container;
  std::vector<std::shared_ptr<SkipNode>> cur_container;
  
  // 双指针流派。
  std::shared_ptr<SkipNode> current_pointer = header_;
  std::shared_ptr<SkipNode> forward_pointer;

  bool found = false;
  size_t target_height = 0;     // 记录首次发现该节点的高度。删除操作将从这个高度开始。

  for(size_t i = MaxHeight; static_cast<int>(i) >= 0; i--) {
    forward_pointer = current_pointer -> Next(i);
    // 遍历该高度所有节点。
    while(forward_pointer != nullptr && compare_(forward_pointer -> Key(), key) == true) {
      current_pointer = forward_pointer;
      forward_pointer = forward_pointer -> Next(i);
    }
    if (forward_pointer != nullptr && compare_(forward_pointer -> Key(), key) == false &&
        compare_(key, forward_pointer -> Key()) == false) {
      found = true;
      target_height = std::max(i, target_height);
      cur_container.push_back(current_pointer);
      next_container.push_back(forward_pointer -> Next(i));
    }
  }
  // 寻找到目标节点，进行删除操作。
  if(found == true) {
    for(size_t i = target_height; static_cast<int>(i) >= 0; i--) {
      current_pointer = cur_container[target_height - i];
      forward_pointer = next_container[target_height - i];
      current_pointer->SetNext(i,forward_pointer); 
    }
    forward_pointer.reset();
    size_--;
  }
  return found;
}

时空复杂度分析

您好，欢迎来到对数学不好的人最痛苦的地方。

时间复杂度分析

时间复杂度分析首先摆出结论：平均的时间复杂度均为 \(O(\log{n})\).
我们首先根据我们的搜索路径进行反向分析，并且假设我们位于节点 \(x\) 的第 \(i\) 层上。基于我们的假设，我们有：

1. 节点无法知道左边节点的高度，以及自身的高度。
2. 节点的高度至少为 \(i\)。
3. 节点不是头结点。
4. 悲观分析：链表无限长，无限高。

这样我们再进行反向追溯我们的搜索路径时，我们就有两种选择：

1. 节点的高度为 \(i\)， 我们需要向左边前进到同层的前驱节点。
2. 节点的高度大于 \(i\)， 我们需要继续向上爬升。

这样我们就可以假设一个搜索代价 \(C(k)\)，代表的是一条搜索路径在无限高的跳表中下降k层(也就是我们反向追溯上升k层)的期望代价。我们很显然地可以知道，第0层为终点，不再有可能下降。因此我们有：

\[\begin{aligned} \begin{cases} C(0) &= 0\\ C(k) &= p(\text{向上爬升的期望代价})+(1-p)(\text{同级前进的期望代价})\\ &= p(1+C(k-1))+(1-p)(C(k)+1) \end{cases} \end{aligned} \]

这样我们代入就可以得到 \(C(k)=\dfrac{k}{p}\)。将我们的悲观分析放宽到一个具有 \(n\) 个元素的链表，这样从第 \(1(0)\) 层到第 \(L(n)(L(n)-1)\) 层的搜索期望上界就是 \(C(L(n)-1) = \dfrac{L(n)-1}{p}\).

接下来我们需要继续回溯直到头结点的最大高度。我们仍然还是拥有两种情况，向左回溯或者向上攀升。我们先考虑向左回溯需要经过多少步，也就是判断 \(L(n)\) 有多少节点。

我们设在 \(L(n)\) 层的期望节点数为 \(1/p\)。根据生成随机高度的规则，每一层的节点有 \(p\) 的概率高升，有 \(1-p\) 的概率原地踏步。这样我们就设 \(E[k]\) 为每层节点的期望数目。我们有：

\[\begin{aligned} E[1] &= n\\ E[k] &= np^{k-1}\\ E[L(n)] &= np^{L(n)-1} =\dfrac{1}{p} \end{aligned} \]

这样很容易得出 \(L(n) = \log_{\frac{1}{p}}n\). 在 \(L(n)\) 层向左走的期望步数也就是 \(1/p\)。

接下来判断向上走。向上走的概率我们需要计算高于 \(k\) 层的概率是多少，从而计算出最高层数的一个上界。

首先我们需要计算一下节点最高出现在第 \(i\) 层的概率。对于一个节点，它将有 \(\dfrac{1}{p}\) 的概率继续上升，\((1-p)\) 的概率留在此处。这样它需要选择上升 \(i-1\) 次，最后选择不上升。这样我们有：

\[\begin{aligned} p(1) &= 1 - p\\ p(i) &= p^{i-1}(1-p) \end{aligned} \]

这样我们就有节点小于等于 \(k\) 的概率为

\[\begin{aligned} \sum_{i=1}^{k}p(i) &= (1-p)(1+p+\cdots+p^{k-1})\\ &=1-p^k \end{aligned} \]

这样对于一个具有 \(n\) 个节点的跳表来说，\(n\) 个节点都小于等于 \(k\) 的概率为 \((1-p^k)^n\)。这样列表的最高高度大于 \(k\) 的概率为 \(1-(1-p^k)^n\)，我们通过近似可以得知其上界为 \(np^k\). 这样对于期望最高层级我们有期望计算。我们需要注意的是 \(np^{L(n)-1}=1/p\).

\[\begin{aligned} E[M] &= L(n) + \sum_{i=L(n)+1}^{\infty}iP(\text{节点出现在第i层})\\ &= L(n) + \sum_{i=L(n+1)}^{\infty}P(节点出现在大于等于第i层)\\ &= L(n) + \sum_{i=L(n)}^{\infty}P(节点出现在大于第i层)\\ &\leqslant L(n) + np^{L(n)} + np^{L(n)+1}+\cdots\\ &= L(n) + \dfrac{np^{(L(n))}}{1-p}=L(n)+\dfrac{1}{1-p} \end{aligned} \]

这样我们还需要攀升 \(\dfrac{1}{1-p}\) 次。

这样我们的总步数就是从1攀升到L-1，L-1向左走和继续向上到达头结点最高点的步数之和。

\[\begin{aligned} Cost &\leqslant \dfrac{L(n)-1}{p} + \dfrac{1}{p} + \dfrac{1}{1-p} \\ &=L(n)/p + 1/(1-p)\\ &=\dfrac{\log_{1/p}n}{p}+\dfrac{1}{1-p}=O(\log{n}) \end{aligned} \]

这样就完成了时间复杂度的证明。

空间复杂度

对于一个跳表，每个节点出现高度为 \(k\) 的概率为 \(p^{k-1}(1-p)\). 这样对于一个节点，其所具有的副本数目为：

\[E[N] = \sum_{k=1}^{\infty}(1-p)p^k = 1 \]

这样平均的空间复杂度就是 \(O(n)\)。

应用

在许多DB中，跳表都用来记录有序集合，另辅以哈希集合来记录对元素的映射。例如LevelDB。作为键值储存的Redis也使用跳表来维护有序集合。