浅谈FHQ-Treap

确实 FHQ-Treap 不知道比隔壁 Splay 好多少，码量少，常数小。

前置知识

C++

BST

Head

原理&代码实现

FHQ Treap 不是通过旋转来保持平衡的，而是通过分裂和合并。 FHQ Treap 会按二叉搜索树一样根据键值排序结点，并且随机赋给每个结点一个优先级，按照二叉堆的顺序排序结点（这里用大根堆）。Treap 通过旋转，使平衡树同时满足这两个性质，从而达到平衡。而 FHQ Treap 通过调用合并函数时使平衡树满足堆序，实现原理与 Treap 不同。

新建一个节点也就是赋值与初始化各项信息,当然需要返回节点编号作为描述这个节点的信息

int new(int val){
	tr[++ind].val=val;//权值
	tr[ind].rnd=rand();//优先级
	tr[ind].siz=1;//子树大小
	return ind;
}

关于为什么优先级随机的话树高期望为 $O(\log n)$ 的证明先咕咕咕。
最基本的上传合并左儿子和右儿子的大小（当然也可以维护权值信息）：

void pushup(int x){
	int ls=tr[x].ls;
	int rs=tr[x].rs;
	tr[x].siz=tr[ls].siz+tr[rs].siz+1;//当然要算上自己所以+1
}

Part 1：Split(分裂)

分为两种，各有各的功能：

• 按权值分裂：分成两颗子树，一颗子树的值全部 $\leq val$ 另一颗树全部 $\geq val$。
• 按大小分裂，使得一颗子树大小为 $size$ 另一颗为剩下的。

按权值大小分裂：

例如按权值 $25$ 分裂：

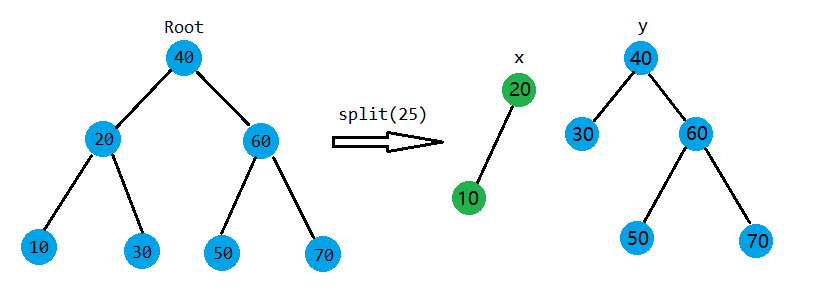
可以发现所以比 $25$ 值小的树都在以 $x$ 为根的树上。

那我们该怎么写捏？假设 $X,Y$ 是分裂出来的两颗树的根，我们当前到了点 $root$ 则如果 $Val_{root} \leq val$ 则它应该在 $X$ 树上，否则就在 $Y$ 树上。如果假设成立，则仍需要向右子树去寻找是否有节点 $z$ 使得 $Val_{root} \leq z \leq val$ 即在 $root$ 的右子树里是否有比当前值大，但权值仍比 $val$ 小的节点。

void split_val(int x,int val,int &a,int &b){
 	if(!x){a=b=0;return;}
	if(tr[x].val<=val){
		split_val(tr[x].rs,val,tr[x].rs,b);
		a=x;
	}else{
		split_val(tr[x].ls,val,a,tr[x].ls);
		b=x;
 	}pushup(x);
}

按大小分裂：

和按权值分裂相似，只是在 $siz_{ls} < siz$ 时，也就是递归右子树时需要将 $siz-siz_{ls}$ 这是显然的。

void split(int root, int sze, int &x, int &y) {
	if (root == 0) {
		x = y = 0;
		return;
	}
	if (Tree[Tree[root].Left].Size + 1 <= sze) {
		x = root;
		split(Tree[root].Right, sze - Tree[Tree[root].Left].sze - 1, Tree[root].Right, y);
	} else {
		y = root;
		split(Tree[root].Left, sze, x, Tree[root].Left);
	}
	pushup(root);
}

Part 2：merge（合并）

如图

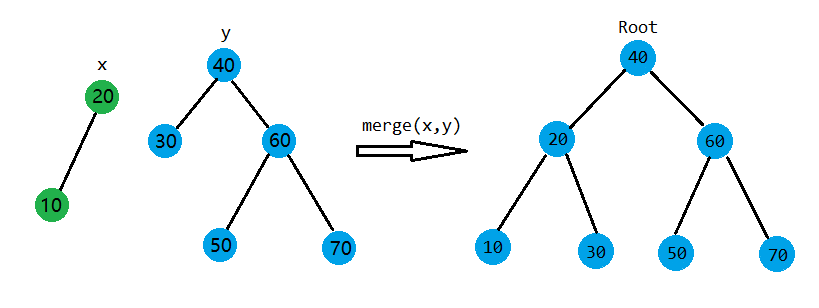
在合并时，需要满足 $X,Y$ 两颗树中 $X$ 的最大值小于 $Y$ 的最小值。

这时只需要按优先级合并就好啦，优先级大的在上面，小的在下面并不会影响 BST 的性质。

void merge(int x,int y,int &a){
	if(!x || !y){a=x+y;return;}
	if(tr[x].rnd<tr[y].rnd){
		merge(tr[x].rs,y,tr[x].rs);
		a=x;pushup(x);
	}else{
		merge(x,tr[y].ls,tr[y].ls);
		a=y;pushup(y);
	}
}

各种操作

平衡树的基本操作是很简单的。
但由这些操作衍生出的操作就可多了去了。

插入：

假设插入的值 $val$，把树按权值 $val-1$ 分裂成两棵树，最后新建节点合并起来就好。

void insert(int i){
	split_val(root,i-1,a,b);
	merge(a,new(i),a);
	merge(a,b,root);
}

删除：

假设删除值 $val$ 则把树按 $val$ 分裂成 $X,Y$ 两颗，再把树 $X$ 按 $val-1$ 分成 $X,Z$ 两颗树，此时树 $Z$ 上的所有权值都为 $val$ 如果只删一个点那么直接将树 $Z$ 的左右儿子合并然后赋值给 $Z$,如果删除所有是这个值的点则直接合并 $X,Y$ 就好啦。

void remove(T key) {
    int x, y, z;
    split(Root, key, x, z);
    split(x, key - 1, x, y);
    if (y) { // 如果删除所有，就直接去掉这个if语句块，并且下面的只合并x, z
        y = merge(Tree[y].Left, Tree[y].Right);
    } 
    Root = merge(merge(x, y), z);
}

指定权值查排名：

假设查询的值为 $val$ 则按 $val-1$ 分裂成 $X,Y$ 最后查询 $X$ 树的大小然后 +1 就好啦。

int rank(T key) {
    int x, y, ans;
    split(Root, key - 1, x, y);
    ans = Tree[x].Size + 1;
    Root = merge(x, y);
    return ans;
}

查询指定排名的值:

写法一：

从根节点开始，用左子树的 $size+1$ 确定答案，三种情况。

• $size+1 > rank$ 在左子树。
• $size+1 < rank$ 在右子树。
• $size+1 = rank$ 找到答案。

	int root = Root;
	while (true) {
        if (Tree[Tree[root].Left].Size + 1 == r) {
            break;
        } else if (Tree[Tree[root].Left].Size + 1 > r) {
            root = Tree[root].Left;
        } else {
            r -= Tree[Tree[root].Left].Size + 1;
            root = Tree[root].Right;
        }
    }
    return Tree[root].Key;

写法二：

按排名分裂成三棵树，去中间那颗的值。

// 这里的split是按大小分裂
T at(int r) {
    int x, y, z;
    split(Root, r - 1, x, y);
    split(y, 1, y, z);
    T ans = Tree[y].Key;
    Root = merge(merge(x, y), z);
    return ans;
}

很明显，写法一更快，写法二码量小。

前驱指小于当前数的最大值
后继指大于当前数的最小值

查询前驱：

按 $val-1$ 分裂，在 $val-1$ 那棵树上一直往右儿子走，走到叶子结点就是前驱。

    int x, y, root;
    T ans;
    split(Root, key - 1, x, y);
    root = x;
    while (Tree[root].Right) root = Tree[root].Right;
    ans = Tree[root].Key;
    Root = merge(x, y);
    return ans;

查询后继：

后继同理。

询问一个数是否存在：

按 $val$ 分裂成三棵树，看中间那颗树大小是否为 0。

例题：

文艺平衡树

对于区间翻转先咕咕咕。

参考文献:

ctjcalc大佬的博客。