Splay学习笔记

看了半天的 Splay 都没看懂

引入

Splay 树, 或 伸展树，是一种平衡二叉查找树，它通过 Splay/伸展操作 不断将某个节点旋转到根节点，使得整棵树仍然满足二叉查找树的性质，能够在均摊 \(O(\log N)\) 时间内完成插入，查找和删除操作，并且保持平衡而不至于退化为链。

---摘自 OI Wiki.

Splay 树，是一种二叉搜索树（BST），可以在保证BST的性质的情况下实现相较于 \(O(n)\) 暴力更为优化的 \(O(\log N)\) 操作。（如果您看懂了就可以跳过这一段惹）

那么现在问题来了，什么是 BST ？先上个图：

没错，这就是一颗 BST （原谅我丑陋的图）

由图我们可以看出，在一颗 BST 中，左子树 的值要 小于 父节点的值，右子树 的值要 大于 父节点的值。这也是 BST（binary search tree）名字的由来——在树中查找一个值所花费的时间期望为 \(O(\log N)\) 。

然而，我们发现在 OI Wiki 中有一句话

并且保持平衡而不至于退化为链

所以 BST 不一定是我们刚才看到的那个样子，它也可能是这样的：

在这种情况下，我们的操作便退化成了 \(O(N)\) ，这肯定是我们不想看到的。所以，如何让这棵树的 高度 变小，便成了我们的下一个问题。

Splay

兜兜转转终于到正文了

所以我们要怎么通过 Splay 来使这颗丑陋的树变 平衡 呢？答案就是 转 ！（雪月花）

咳咳，其实就是我们 Splay 的 rotate 操作。通过让某个点在树上不停的绕它的父节点旋转，最终让我们的树变的平衡。

让我们看看这个旋转的过程是怎么转的：

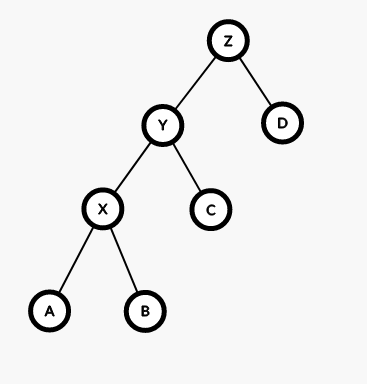
这是一颗 X 节点 待旋转的 BST。

首先我们让 X 节点转到 Y 节点，即切断 X 与 Y 的父子，并让 Y 节点的父节点变为 X 节点的父节点。

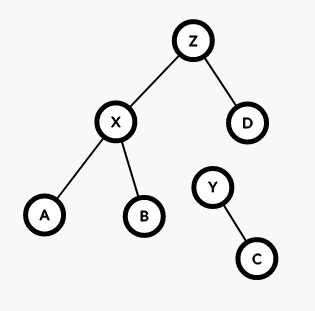
现在 Y 节点就被晾在一旁了，所以我们要拉它回来。于是我们切断 X 与 B 的父子关系，并让 X 与 Y 建立父子关系。

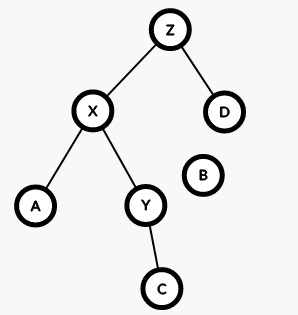
但是现在 B 又被抛弃了，于是我们最后让 Y 与 B 建立，父子关系，那么这个旋转操作便完成啦。

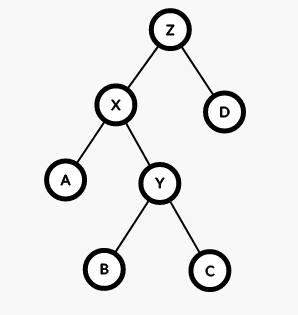
Code

void rotate(ll x){
	ll y=t[x].fa,z=t[y].fa,k=t[y].son[1]==x;//y   z   k
	t[z].son[t[z].son[1]==y]=x;//
	t[x].fa=z;
	t[y].son[k]=t[x].son[k^1];//
	t[t[x].son[k^1]].fa=y;
	t[x].son[k^1]=y;//
	t[y].fa=x;
	pushup(y),pushup(x);
}