FlashAttention全解
LLM大模型训练加速利器FlashAttention详解
-
Attention层是扩展到更长序列的主要瓶颈,因为它的运行时间和内存占用是序列长度的二次方。使用近似计算的Attention方法,可以通过减少FLOP计算次数、甚至于牺牲模型质量来降低计算复杂性,但通常无法实现大比例的加速。
-
FlashAttention没有进行近似计算,所以也没有精度损失。然而,FlashAttention的实际速度仍然和理论上的运算速度差距较大,仅达到理论最大 FLOPs/s 的 25-40%。效率低下的原因主要是不同线程块和warp之间的工作分区不理想,导致低占用率或不必要的共享内存读/写。
为此,2023年7月,论文作者进一步提出了FlashAttention-2,实现了Attention计算速度的大幅度提升。
一、FlashAttention
1.1 硬件基础
-
我们常说的A100 80G,80G指的是GPU中的HBM存储,其上还有更为快速的SRAM,其大小约为20MGB。
-
一次注意力计算分为多步计算过程,第一步 \(QK^T\),第二步\(softmax\),第三步\(\cdot V\),每一步计算产生的中间结果都需要存储到HBM中,需要时在进行读取,其复杂度为\(O(N^2)\)。
-
SRAM是非常有限的,无法把所有的数都加载的SRAM里,序列长度N(Token的数量)通常是以k来计算,4k和8k是比较常见的,某些应用(code)甚至希望能到64k和128k。因此\(N^2\)会增长的非常快。
-
每次计算产生的中间结果都需要\(O(N^2)\)的开销将中间结果移动到HBM中,通信代价 > 计算代价
如何降低通信代价?让更多的操作发生在SRAM上?计算的中间结果,如何才能不传输到HBM?全部在SRAM中进行?
1.2 FlashAttention 核心思想
如何改造计算流程,让中间结果存储到HBM的过程不要发生?
Flash Attention 将计算模块化,将QKV分为若干个模块进行计算,在计算过程中不存储$ N \times N $的矩阵
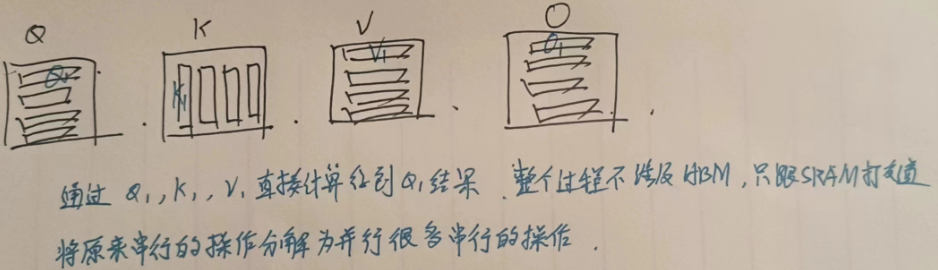
最终只有输出\(O_1\)涉及存储到HBM中。
1.3 计算前提
仅仅是将矩阵进行分块计算这样就可以了吗?No
-
数值稳定性:在计算注意力的过程中,涉及到\(softmax\)操作,\(softmax\)包含指数函数,所以为了避免数值溢出问题,可以将每个元素都减去最大值,对于一个向量来说,我们给每一个数减去相同的任一常量,其\(softmax\)是不变的。
\(m(x):=\max _{i} \quad x_{i}, \quad f(x):=\left[\begin{array}{lll} e^{x_{1}-m(x)} & \ldots & e^{x_{B}-m(x)} \end{array}\right], \quad \ell(x):=\sum_{i} f(x)_{i}, \quad \operatorname{softmax}(x):=\frac{f(x)}{\ell(x)}\)
-
分块计算softmax:同时对于\(softmax\)操作是按行计算的,如果对齐进行分块,那么每行的最大值如果只考虑分块后的最大值就产生了偏差,需要维护每行的最大值用于分块以及上述数值的稳定性计算。
我们考虑将一行分为两部分的情况,即原本的一行数据 \(x \in \mathbb{R}^{2 B}=\left[x^{(1)}, x^{(2)}\right]\)
考虑整行正确的 \(f(x^{(1)}) = e^{x^{(1)}-max(x)}\)
有偏差的考虑分块的 \(f'(x^{(1)}) = e^{x^{(1)}-max(x^{(1)})}\)
如何进行纠正?\(f(x^{(1)}) =f'(x^{(1)}) \times e^{max(f'(x^{(1)})) - max(x)}\)
所以说,分块计算之后,要进行纠正,需要维护整行的\(max\)值。
1.4 FlashAttention 算法
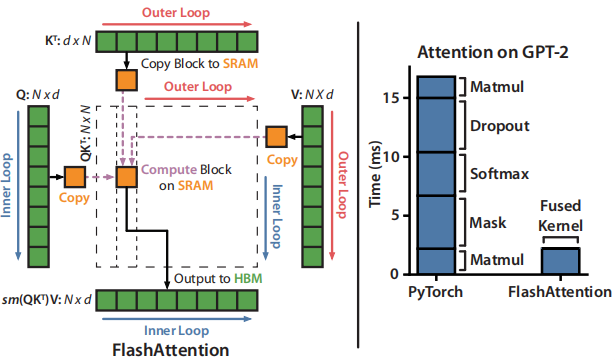
简要描述:外层循环遍历\(K^T\),内层循环遍历\(Q\)
\(Q\)的第一块(按行拆分)和\(K^T\)的第一块(按列拆分)计算得到中间结果\(S\)中\((0, 0)\)的结果
\(Q\)的第二块(按行拆分)和\(K^T\)的第一块(按列拆分)计算得到中间结果\(S\)中\((1, 0)\)的结果
\(Q\)的第三块(按行拆分)和\(K^T\)的第一块(按列拆分)计算得到中间结果\(S\)中\((2, 0)\)的结果
\(Q\)的第三块(按行拆分)和\(K^T\)的第一块(按列拆分)计算得到中间结果\(S\)中\((3, 0)\)的结果
这里应该是可以并行计算的,因为这是中间结果的第一列,不涉及softmax操作,暂时还未涉及到分块计算softmax纠正偏差的问题。
当外层循环计算到\(K^T\)的第二块(按列拆分)时,就会开始填充中间结果\(S\)的第二列,这时有了第一列和第二列的结果,就需要进行\(softmax\)纠正偏差。
至此,后面计算到中间结果的每列时,每当有新的中间结果加入时,都需要对该中间结果所在的行进行纠正错误。
纠正方法:\(\times e^{max(x_{sec}) - max(x)}\)
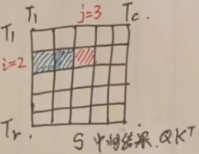
每次循环计算时,将\(K_j, V_j\)加载到SRAM,占据SRAM的50%的存储,将\(Q_i,O_i\)加载进SRAM,占据另一半的显存。\(l_i, m_i\)比较小,按作者的说法可以放进寄存器。

初始化
按列拆分,每个块的大小为 \(B_c = \left\lceil\frac{M}{4 d}\right\rceil\),将\(K, V\)拆分为\(T_{c}=\left\lceil\frac{N}{B_{c}}\right\rceil\)个列块,形状 \(B_c \times d\)。
按行拆分,每个块的大小为 \(B_{r}=\min \left(\left\lceil\frac{M}{4 d}\right\rceil, d\right)\),将\(Q\)拆分为 \(T_{r}=\left\lceil\frac{N}{B_{r}}\right\rceil\) 个行块,形状 \(B_r \times d\)。
将\(O\)按行拆分为 \(T_r\) 个块,形状 \(B_r \times d\)。
将\(l,m\)均拆分为 \(T_r\) 个块,大小为 \(B_r\) 的一维向量。
将 \(Q_i, O_i, l_i, m_i\) 从HBM移动到SRAM
计算 \(S_{ij} = Q_iK_j^T\)
修正每个行块的 \(\tilde{m}_{i j}\),修正每个块的中间计算结果 \(\tilde{\mathbf{P}}_{i j}=\exp \left(\mathbf{S}_{i j}-\tilde{m}_{i j}\right)\),修正每行的累积和 \(\tilde{\ell}_{i j}\)
更新每块
二、FlashAttention-2
- 去年7月,FlashAttention-2发布,相比第一代实现了2倍的速度提升,比PyTorch上的标准注意力操作快5~9倍。
- 在H100上仅实现了理论最大FLOPS 35%的利用率。
- FlashAttention(以及FlashAttention-2)通过减少内存读写次数,开创了一种在GPU上加速注意力机制的方法,现在大多数库都使用它来加速Transformer的训练和推理。这使得大语言模型的上下文长度在过去两年中大幅增加,从2-4K(如GPT-3、OPT)扩展到128K(如GPT-4),甚至达到1M(如Llama 3、Gemini 1.5 Pro)。
2.1 硬件特性
GPU存在大量的线程(被称为kernel)用于执行一个操作。线程被组织为线程块,线程块被调度在 streaming multiprocessors (SMs) 上运行。
在每个线程块内部,线程被分组为 warps (包含32个线程的线程组)。
warp 内的线程可以通过 fast shuffle instructions 进行通信或协同执行矩阵乘法。
线程块内的warps 可以通过对共享内存读写进行通信。
每个线程 (kernel) 从HBM 中加载输入到寄存器和SRAM中计算,然后将输出写回 HBM。
2.2 标准的注意力实现
给定输入序列 \(\mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{N \times d}\),计算注意力输出 \(\mathbf{O} \in \mathbb{R}^{N \times d}\).
中间计算过程 \(\mathbf{S}=\mathbf{Q} \mathbf{K}^{\top} \in \mathbb{R}^{N \times N}, \quad \mathbf{P}=\operatorname{softmax}(\mathbf{S}) \in \mathbb{R}^{N \times N}, \quad \mathbf{O}=\mathbf{P V} \in \mathbb{R}^{N \times d}\)
softmax是基于每行进行操作的。
对于多头注意(MHA),这个相同的计算是在多个头部上并行执行的,并在批处理维度(批处理中输入序列的数量)上并行执行的。
注意力的反向传播过程如下。设 \(\mathrm{dO} \in \mathbb{R}^{N \times d}\) 是O相对于某些损失函数的梯度。然后根据链式规则(即反向传播):
\(\mathbf{d V}=\mathbf{P}^{\top} \mathbf{d} \mathbf{O} \in \mathbb{R}^{N \times d}\)
\(\mathbf{d} \mathbf{P}=\mathbf{d} \mathbf{O} \mathbf{V}^{\top} \in \mathbb{R}^{N \times N}\)
\(\mathbf{d S}=\operatorname{dsoftmax}(\mathbf{d} \mathbf{P}) \in \mathbb{R}^{N \times N}\)
\(\mathrm{dQ}=\mathrm{dSK} \in \mathbb{R}^{N \times d}\)
\(\mathbf{d K}=\mathbf{Q d} \mathbf{S}^{\top} \in \mathbb{R}^{N \times d}\)
dsoftmax是逐行应用的softmax的梯度。
对于向量\(s, p\),如何从输出梯度 \(d_p\)计算输入梯度 \(𝑑_𝑠\)?
\(d s=\left(\operatorname{diag}(p)-p p^{\top}\right) d p\)
\(diag(p)\) 是一个对角矩阵,其对角线上的元素是 \(𝑝\) 的元素。
标准的注意实现将矩阵\(S\)和\(P\)存储到HBM,这需要 \(O(N^2)\)内存。通常𝑁≫𝑑(通常𝑁在1k-8k左右,𝑑在64-128左右)。
标准注意实现:
(1)调用矩阵乘(GEMM)计算 \(S=QK^T\),将结果写入HBM
然后(2)从HBM加载\(S\)并计算softmax,并将结果\(P\)写入HBM,
最后(3)调用GEMM计算 \(O = PV\)。
由于大多数操作受到内存带宽的限制,大量的内存访问转化为 slow wall-clock time。
此外,由于必须实现S和P,所需的内存是 \(O(N^2)\)。此外,我们必须保存 \(P\in\mathbb{R}^{N\times N}\) 用于反向传播计算梯度。
2.3 Flash Attention-1
2.3.1 前向传播
FlashAttention 应用传统的 tiling 来减少内存IO:
- 从HBM加载 blocks of inputs 到SRAM
- 计算对 block 的 attention
- 更新输出,而不需要将较大的中间矩阵S和P写入HBM
由于 softmax 耦合 entire row 或 blocks of row (整行或块内的行,指softmax操作特性),online softmax 可以将注意力计算分割成块,并重新调整每个块的输出,最终得到正确的结果(无近似值)。
通过显著减少内存读取/写入量,FlashAttention 实现了优化基线注意实现的 2-4 倍的 wall-clock 加速。
online softmax如何在注意力中使用?
为了简单起见,仅考虑注意力矩阵\(S\)的一个 row block \([s^{(1)} \ s^{(2)}]\),其中 \(s^{(1)}, s^{(2)} \in \mathbb{R}^{B_r \times B_c}\),我们想要计算这个row block的softmax以及与value\(\left[\begin{array}{l} \mathbf{V}^{(1)} \\ \mathbf{V}^{(2)} \end{array}\right]\)的乘积,\(\mathbf{V}^{(1)}, \mathbf{V}^{(2)} \in \mathbb{R}^{B_c \times d}\),标准的softmax计算如下:
- \(m=\max \left(\operatorname{rowmax}\left(\mathbf{S}^{(1)}\right), \operatorname{rowmax}\left(\mathbf{S}^{(2)}\right)\right) \in \mathbb{R}^{B_{r}}\) \(m\)这里是整行的最大值
- \(\ell=\operatorname{rowsum}\left(e^{\mathbf{S}^{(1)}-m}\right)+\operatorname{rowsum}\left(e^{\mathbf{S}^{(2)}-m}\right) \in \mathbb{R}^{B_{r}}\) \(l\) 计算的是整行的指数和,减去最大值为了防止溢出
- \(\mathbf{P}=\left[\begin{array}{ll} \mathbf{P}^{(1)} & \mathbf{P}^{(2)} \end{array}\right]=\operatorname{diag}(\ell)^{-1}\left[\begin{array}{ll} e^{\mathbf{S}^{(1)}-m} & e^{\mathbf{S}^{(2)}-m} \end{array}\right] \in \mathbb{R}^{B_{r} \times 2 B_{c}}\) 计算softmax,除指数和,通过乘以 \(diag(l)^{-1}\) 实现除法
- \(\mathbf{O}=\left[\begin{array}{ll} \mathbf{P}^{(1)} & \mathbf{P}^{(2)} \end{array}\right]\left[\begin{array}{l} \mathbf{V}^{(1)} \\ \mathbf{V}^{(2)} \end{array}\right]=\operatorname{diag}(\ell)^{-1} e^{\mathbf{S}^{(1)}-m} \mathbf{V}^{(1)}+e^{\mathbf{S}^{(2)}-m} \mathbf{V}^{(2)} \in \mathbb{R}^{B_{r} \times d}\) 计算输出\(O\)
Online softmax 计算每个块的“local”softmax,然后重新缩放以得到正确的输出
- \(m^{(1)}=\operatorname{rowmax}\left(\mathbf{S}^{(1)}\right) \in \mathbb{R}^{B_{r}}\) 第一个块的最大值 \(m^{(1)}\)
- \(\ell^{(1)}=\operatorname{rowsum}\left(e^{\mathbf{S}^{(1)}-m^{(1)}}\right) \in \mathbb{R}^{B_{r}}\) 第一个块的指数和 \(l^{(1)}\)
- \(\tilde{\mathbf{P}}^{(1)}=\operatorname{diag}\left(\ell^{(1)}\right)^{-1} e^{\mathbf{S}^{(1)}-m^{(1)}} \in \mathbb{R}^{B_{r} \times B_{c}}\) 第一个块的softmax值
- \(\mathbf{O}^{(1)}=\tilde{\mathbf{P}}^{(1)} \mathbf{V}^{(1)}=\operatorname{diag}\left(\ell^{(1)}\right)^{-1} e^{\mathbf{S}^{(1)}-m^{(1)}} \mathbf{V}^{(1)} \in \mathbb{R}^{B_{r} \times d}\) 第一个块的输出 \(O^{(1)}\)
- \(m^{(2)}=\max \left(m^{(1)}, \operatorname{rowmax}\left(\mathbf{S}^{(2)}\right)\right)=m\) 计算第二个块的最大值,将第一个块的最大值也要考虑进去
- \(\ell^{(2)}=e^{m^{(1)}-m^{(2)}} \ell^{(1)}+\operatorname{rowsum}\left(e^{\mathbf{S}^{(2)}-m^{(2)}}\right)=\operatorname{rowsum}\left(e^{\mathbf{S}^{(1)}-m}\right)+\operatorname{rowsum}\left(e^{\mathbf{S}^{(2)}-m}\right)=\ell\) 更新指数和,\(m^{(2)}\)现在更新为了整行的最大值,最先前已经计算出的第一块的指数和进行纠正缩放,再加上第二块的指数和,最终得到整行的指数和
- \(\tilde{\mathbf{P}}^{(2)}=\operatorname{diag}\left(\ell^{(2)}\right)^{-1} e^{\mathbf{S}^{(2)}-m^{(2)}}\) 第二块的softmax值
- \(\mathbf{O}^{(2)}=\operatorname{diag}\left(\ell^{(1)} / \ell^{(2)}\right)^{-1} \mathbf{O}^{(1)}+\tilde{\mathbf{P}}^{(2)} \mathbf{V}^{(2)}=\operatorname{diag}\left(\ell^{(2)}\right)^{-1} e^{s^{(1)}-m} \mathbf{V}^{(1)}+\operatorname{diag}\left(\ell^{(2)}\right)^{-1} e^{s^{(2)}-m} \mathbf{V}^{(2)}=\mathbf{O}\) 计算整行的输出,对之前使用局部最大值计算出来的\(O^{(1)}\)进行纠正缩放,再加上第二块的输出\(\tilde{\mathbf{P}}^{(2)} \mathbf{V}^{(2)}\)
下图为 FlashAttention 使用 online softmax 开启 tiling 减少内存读写。
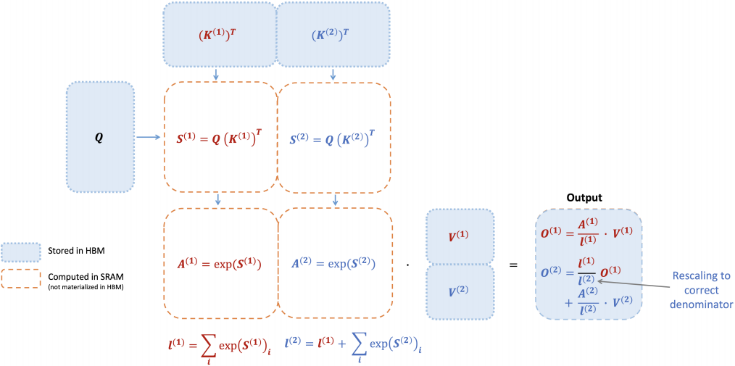
图中,键K和值V分为了两个块。
2.3.2 反向传播
-
在反向传播中,一旦输入的Q、K、V已经加载到SRAM,通过重新计算注意力矩阵S和P的值,FlashAttention 避免了存储较大的中间值。
通过不保存大小为𝑁×𝑁的大矩阵S和P,FlashAttention 产生10-20倍内存节省,取决于序列长度(序列长度𝑁为线性内存,而不是二次内存)。由于减少内存读写,反向传播也实现了2-4倍的wall-clock加速。
-
反向传播也应用了tiling。虽然反向传播在概念上比前向传播更简单(没有softmax重缩放),但实现明显更复杂。
这是因为在SRAM中有更多的值需要保留,以便在反向传播中执行5个矩阵乘法,而在前向传播中只有2个矩阵乘法。
2.4 FlashAttention-2
我们描述了FlashAttention-2算法,它包括对 FlashAttention 的一些调整,以减少 non-matmul FLOPs。
然后,我们将描述了如何在不同的线程块上并行化计算,以充分利用GPU资源。
最后,我们描述了在一个线程块内的不同warp之间划分工作,以减少共享内存的访问量。
2.4.1 算法调整
调整了FlashAttention的算法以减少 the number of non-matmul FLOPs.
这是因为现代 GPUs 有专门的计算单元( 例如,Nvidia图形处理器上的 Tensor Cores ),可以使乘法更快。
例如,A100 GPU的FP16/BF16 matmul的最大理论吞吐量为 312TFLOPs/s,而非matmul FP32的理论吞吐量只有19.5 TFLOPs/s。
另一种角度思考,每个非矩阵 FLOP 比一个矩阵FLOP 昂贵16×。
为了保持高吞吐量(例如,超过最大理论TFLOPs/s的50%),我们希望花尽可能多的时间在matmul FLOPs上。
2.4.1.1 前向传播
重新回到online softmax trick,做出了两个小的调整以减少非乘法FLOPs
-
在2.3.1 FlashAttention online softmax 中, 对于\(O^{(2)}\)的计算, 我们先对第二部分的中间计算结果\(\tilde{\mathbf{P}}^{(2)}\)进行了缩放 \(\tilde{\mathbf{P}}^{(2)}=\operatorname{diag}\left(\ell^{(2)}\right)^{-1} e^{\mathbf{S}^{(2)}-m^{(2)}}\)
然后在计算最终的输出 \(O^{(2)}\) 时, 又对第一部分的输出结果 \(O^{(1)}\) 进行了缩放调整 \(\operatorname{diag}\left(\ell^{(1)} / \ell^{(2)}\right)^{-1} \mathbf{O}^{(1)}\)
FlashAttention-2 对此进行改进, 避免对两项都进行缩放
方法是维护未缩放的 \(O^{(2)}\) 并保持统计信息 \(\ell^{(2)}\),具体计算如下:
\(\tilde{\mathbf{O}}^{(2)}=\operatorname{diag}\left(\ell^{(1)}\right)^{-1} \mathbf{O}^{(1)}+e^{\mathbf{S}^{(2)}-m^{(2)}} \mathbf{V}^{(2)}\) 这里并没有计算完整的\(O^{(2)}\), 没有缩放
只在循环的结束时, 通过 \(diag(\ell^{(last)})^{-1}\) 缩放最终的 \(\tilde{\mathbf{O}}^{\text {(last) }}\) 得到正确的output
-
在反向传播过程中, 不再需要保存最大值 \(m^{(j)}\) 和指数和 \(\ell^{(j)}\), 只需要存储 对数指数和 \(L^{(j)}=m^{(j)}+\log \left(\ell^{(j)}\right)\)
同样是一个简单的两个块的示例, online softmax trick 现在变为:
- \(m^{(1)}=\operatorname{rowmax}\left(\mathbf{S}^{(1)}\right) \in \mathbb{R}^{B_{r}}\) 计算第一部分的最大值
- \(\ell^{(1)}=\operatorname{rowsum}\left(e^{\mathbf{S}^{(1)}-m^{(1)}}\right) \in \mathbb{R}^{B_{r}}\) 计算第一部分的局部指数和
- \(\mathbf{O}^{\tilde{(1)}}=e^{\mathbf{S}^{(1)}-m^{(1)}} \mathbf{V}^{(1)} \in \mathbb{R}^{B_{r} \times d}\) 计算未缩放的\(\mathbf{O}^{\tilde{(1)}}\), 相当于这时还没有进行softmax
- \(m^{(2)}=\max \left(m^{(1)}, \operatorname{rowmax}\left(\mathbf{S}^{(2)}\right)\right)=m\) 计算第二部分的最大值, 由于上述提到,中间不再维护最大值进行缩放纠正,当前仅两个分块, 所以这里是再最后时刻才会统计最大值 !
- \(\ell^{(2)}=e^{m^{(1)}-m^{(2)}} \ell^{(1)}+\operatorname{rowsum}\left(e^{\mathbf{S}^{(2)}-m^{(2)}}\right)=\operatorname{rowsum}\left(e^{\mathbf{S}^{(1)}-m}\right)+\operatorname{rowsum}\left(e^{\mathbf{S}^{(2)}-m}\right)=\ell\) 有了最终的最大值, 对先前的指数和进行缩放调整, 并计算当前的指数和
- \(\tilde{\mathbf{P}}^{(2)}=\operatorname{diag}\left(\ell^{(2)}\right)^{-1} e^{\mathbf{S}^{(2)}-m^{(2)}}\) 对最后一部分进行缩放, 应用softmax
- \(\tilde{\mathbf{O}}^{(2)}=\operatorname{diag}\left(e^{m^{(1)}-m^{(2)}}\right)^{-1} \tilde{\mathbf{O}}^{(1)}+e^{\mathbf{S}^{(2)}-m^{(2)}} \mathbf{V}^{(2)}=e^{s^{(1)}-m} \mathbf{V}^{(1)}+e^{s^{(2)}-m} \mathbf{V}^{(2)}\) 对先前的\(\tilde{\mathbf{O}}^{(1)}\)进行缩放, 并加上当前块的输出
- \(\mathbf{O}^{(2)}=\operatorname{diag}\left(\ell^{(2)}\right)^{-1} \tilde{\mathbf{O}}^{(2)}=\mathbf{O}\) 对\(\tilde{\mathbf{O}}^{(2)}\)进行缩放, 得到最终正确的\(O^{(2)}\)
- 第6步 使用全局的指数和 对第二部分进行缩放, 这里的计算结果已经是正确的结果了, 后续没有用到 \(\tilde{\mathbf{P}}^{(2)}\) 为什么还需要计算这一步

结合上述算法, 再次对核心的计算部分进行总结:
对于每个块,
计算当前块为止的最大值 \(m_i^{(j)}\)
计算 \(\tilde{\mathbf{P}}_{i}^{(j)}=\exp \left(\mathbf{S}_{i}^{(j)}-m_{i}^{(j)}\right)\), 称它为未缩放的指数部分
计算 \(\ell_i^{(j)}\) 纠正之前的指数和 + 当前的指数和, 用的最大值是截止到当前块的最大值
计算 \(O_i^{(j)}\) 纠正之前的 \(O_i^{(j-1)}\) + 当前的指数部分×V
在每行的结束时, \(\ell_i^{(T_c)}\) 是整行的纠正过的指数和, \(O_i^{(T_c)}\) 是整行的纠正过的PV和
然后对整行的纠正过的PV和进行统一缩放: \(\mathbf{O}_{i}=\operatorname{diag}\left(\ell_{i}^{\left(T_{c}\right)}\right)^{-1} \mathbf{O}_{i}^{\left(T_{c}\right)}\)
需要缓存的内容:
- 每行结束时, 将\(O_i\) 写入HBM, 将\(L_i\)写入HBM, \(L^{(j)}=m^{(j)}+\log \left(\ell^{(j)}\right)\)
Causal masking
一个常见用例是在自回归语言建模中,我们需要对注意矩阵S应用一个因果掩码 (\(S_{i, j}\) when \(j>i\) is set to \(-∞\))
-
由于FlashAttention和FlashAttention-2已经通过块操作,对于任何所有列索引都超过行索引的块(对于长序列, 近似占到一般的块),我们可以跳过该块的计算。与没有因果掩码的注意力相比,这导致了大约1.7-1.8×的加速。
-
我们不需要对行索引保证严格小于列索引的块应用因果掩码。
This means that for each row, we only need apply causal mask to 1 block (assuming square block). ???
2.4.1.2 反向传播
FlashAttention-2的反向传播过程与FlashAttention几乎相同, 做出了一个小的调整, 仅使用每行的对数指数和\(L\)代替每行的最大值和每行的指数和.
对下图算法总结:
逐元素乘法计算 \(D=\operatorname{rowsum}(\mathbf{d} \mathbf{O} \circ \mathbf{O}) \in \mathbb{R}^{d}\)
反向传播时, 外层遍历列, 内层遍历行
通过\(Q_i, K_j^T\)恢复中间结果 \(\mathbf{S}_{i}^{(j)}=\mathbf{Q}_{i} \mathbf{K}_{j}^{T} \in \mathbb{R}^{B_{r} \times B_{c}}\)
通过\(S_{i, j}, L_i\) 恢复 \(P_i^{(j)}\), \(L^{(j)}=m^{(j)}+\log \left(\ell^{(j)}\right)\)
\(\begin{align} \mathbf{P}_{i}^{(j)} & = \exp \left(\mathbf{S}_{i j}-L_{i}\right) \in \mathbb{R}^{B_{r} \times B_{c}} \\ &= \exp(\mathbf{S}_{i, j} - (m^{(i)} + \log(\ell^{(i)}))) \\ &= \exp(\mathbf{S}_{i, j} - m^{(i)} - \log(\ell^{(i)}) ) \\ &= \exp(\mathbf{S}_{i, j} - m^{(i)}) \times \exp(-\log (\ell^{(i)})) \\ &= \exp(\mathbf{S}_{i, j} - m^{(i)}) \times \frac{1}{\ell^{(i)}} \end{align}\)
由于存储的\(L^{(i)}\)中均为每行的最大值和指数和, 所以这里恢复出来的\(P_i^{(j)}\)即为正确的结果
计算梯度, \(\mathbf{d} \mathbf{V}_{j} \leftarrow \mathbf{d} \mathbf{V}_{j}+\left(\mathbf{P}_{i}^{(j)}\right)^{\top} \mathbf{d} \mathbf{O}_{i} \in \mathbb{R}^{B_{c} \times d}\)
\(\mathbf{d} \mathbf{V}_{j}\) 初始为\(0\)矩阵, 所以这里没问题
计算梯度, \(\mathbf{d} \mathbf{P}_{i}^{(j)}=\mathbf{d} \mathbf{O}_{i} \mathbf{V}_{j}^{\top} \in \mathbb{R}^{B_{r} \times B_{c}}\)
计算梯度, \(\mathrm{dS}_{i}^{(j)}=\mathbf{P}_{i}^{(j)} \circ\left(\mathbf{d P}_{i}^{(j)}-D_{i}\right) \in \mathbb{R}^{B_{r} \times B_{c}}\) ???
计算梯度, \(\mathrm{dQ}_{i} \leftarrow \mathrm{dQ}_{i}+\mathrm{dS}_{i}^{(j)} \mathbf{K}_{j} \in \mathbb{R}^{B_{r} \times d}\)
计算梯度, \(\mathrm{d} \mathbf{K}_{j} \leftarrow \mathrm{dK}_{j}+\mathrm{dS}_{i}^{(j)^{\top}} \mathbf{Q}_{i} \in \mathbb{R}^{B_{c} \times d}\)

多查询注意力MQA 和 分组查询注意力GQA
多个查询头关注同一键和值的头,以减少推理过程中KV缓存的大小。
我们不必复制键和值头,而是隐式地操作头中的索引以执行相同的计算。
在反向传播期间, 需要对隐式重复的不同头部的梯度dK和dV进行求和。
多个查询头共享相同的键和值, 需要对这些共享键和值的梯度进行求和
如果一个键或值被多个查询头使用,那么在反向传播时,需要将这些查询头对应的梯度 𝑑𝐾 和 𝑑𝑉 进行累加,以确保梯度的正确更新。
3. 并行性
4. Warps之间的工作划分
三、FlashAttention-3
-
相比第二代又实现了1.5~2倍的速度提升。
-
FlashAttention-3 将H100的FLOP利用率再次拉到75%。
-
这一版的FlashAttention专攻H100 GPU,只能在H100或H800上运行,不支持其他GPU型号。
四、动画演示
https://www.youtube.com/playlist?list=PLBWdTDczuFNrxnetcH-5CVLRP1u4Ua87m
1. 标准注意力算法--短序列
-
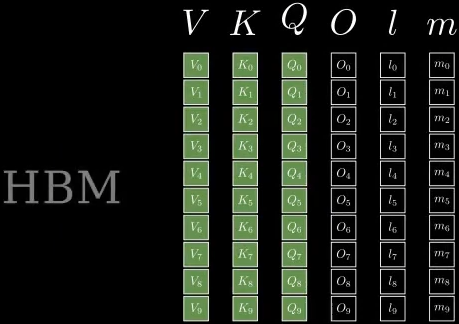
初始时,S、P存储中间计算结果,O存储输出结果,以及Q、K、V均存储在HBM中

-
将Q、K移动到SRAM

-
计算\(QK^T\),依次计算\(Q_0\)和\(K_0, K_1, K_2, K_3, K_4\)的乘积,依次向后填充


-
将计算好的中间结果$S_{0, 0}, S_{0, 1},S_{0, 2},... $,从SRAM移动到HBM。

-
对SRAM中的中间结果计算\(softmax\),每次计算一行 \(S_{0, 0}, ... S_{0, 4}\)
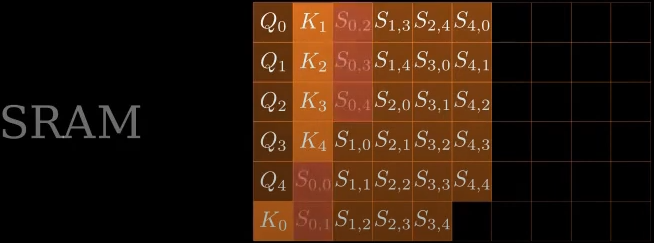

-
\(softmax\)结果\(P\)计算完成后,从SRAM移动到HBM
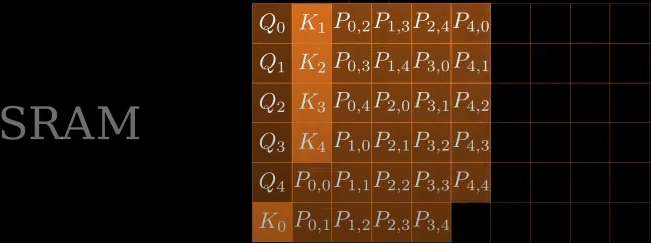

-
将SRAM中存储的\(Q和K\)清空,并将\(V\)从HBM移动到SRAM,进行后续计算
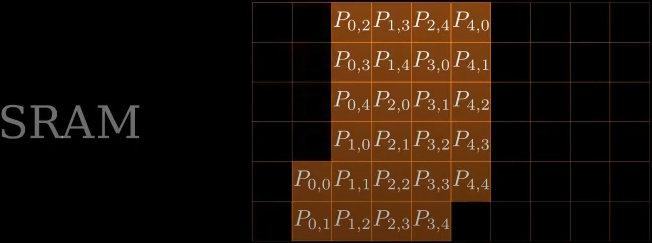
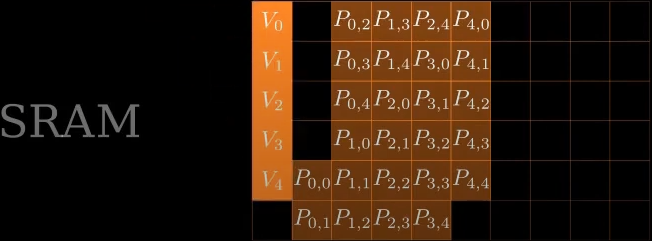
-
计算\(O_i = P_iV\),并将结果从SRAM移动到HBM
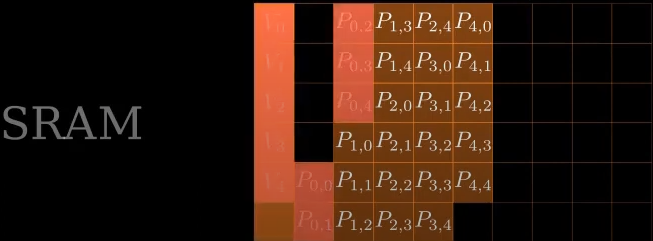
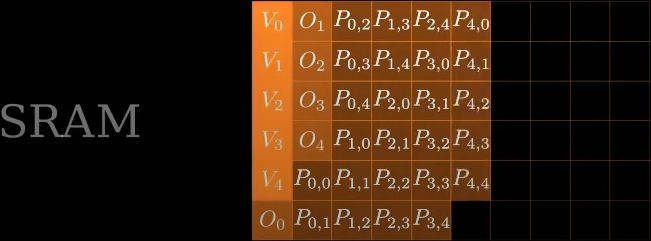

-
最终将SRAM置空

2. 标准注意力算法--长序列
计算过程与短序列一致
3.标准注意力算法--中等长度序列
计算过程与短序列一致
4. Flash Attention算法-长序列
-
初始


 浙公网安备 33010602011771号
浙公网安备 33010602011771号