OO第一章总结

一、程序结构

第一次作业采用了简单的“多项式—项”两层结构，仅考虑了幂函数。另外，对整个表达式的解析与化简完全由多项式类完成，导致多项式类过于臃肿，长度是另两个类的两倍有余，也相当不利于扩展。

 

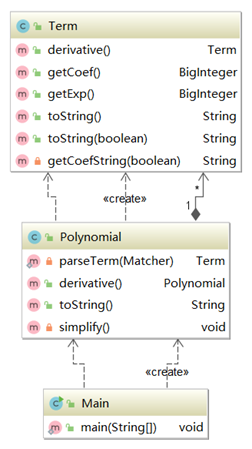
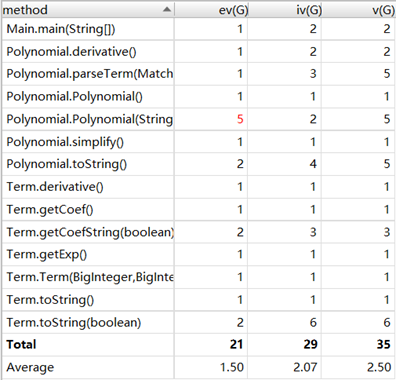
第二次作业全面改变了设计，将表达式分为常数、x、sin函数、cos函数、加和、乘积六类，并设置了一个共同基类，尽可能减少对于某一具体子类的依赖。在“在本次作业中”的指引下，sin和cos也预留了接受非x参数的接口。数据输入方面，我采用了递归下降法，避免了大正则的出现，但复杂度较高的方法也正是主要集中在递归下降的过程中。

 

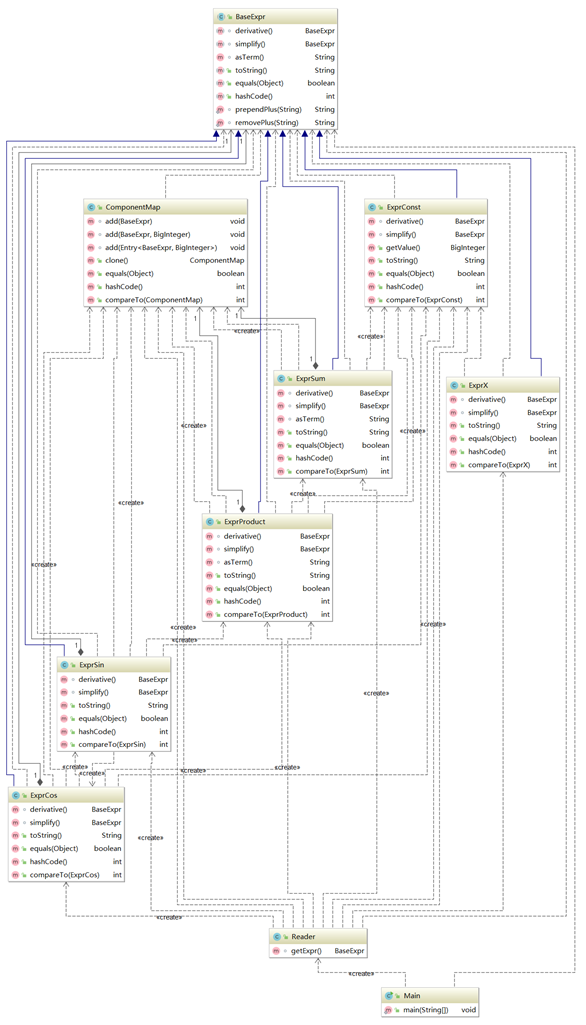
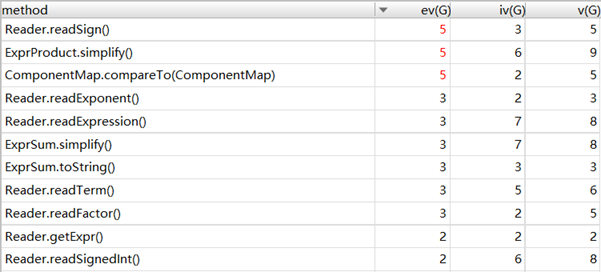
第三次作业的类图与第二次完 全 一 致。事实上，第三次作业是正确性部分耗时最短的一次，主要工作是修改文法及完善复合函数求导规则。至于性能，反正我是追不上数学性质优化的dalao们的，不如肝OS。

二、BUG分析

第一次作业中，由于对指导书中限制的理解错误，被全屋人用非法空白字符打了6下，然后一波同质修复带走，除此外未被测出其他bug。在线下互刀中发现了如下bug：

大正则爆栈。由于贪婪匹配的回溯特性，在输入过长时会超出递归层数限制。

只检查几种特定格式错误。这个方案虽然不像检查正确输入那样要用个巨大的正则，但极容易出现没考虑到的情况。

先合并符号再进行解析。这个本身不是大问题，但与上一条组合就出事了。我在互测中遇到一位同学，先检查了有无超过3个加减号相连的情况（因为+++1合法），然后把所有相连的加减号合并为一个，再进行解析，就放过了+++x这种非法输入。

多次调用toString。例如在加和和乘积的toString中先调用子表达式toString判断是否为0，若非0则再调用一次用于append。在第三次作业中，由于允许表达式的嵌套，这样的写法会导致运行时间随嵌套层数指数级增长，层数稍多就TLE掉。

对可变对象多次求导。部分同学的表达式设计为可变对象，求导方法直接修改自身，这样它的父对象的求导过程就可能将它求了不止一阶的导数。

伪·深拷贝。考虑[xf(x)]’=xf’(x)+f(x)，求导结果中有两部分来自f，对于使用可变对象的同学来说，很容易想到需要把f复制一份再求导，但复制时常出现仅复制了列表而没有复制列表中的元素，甚至共用一个列表的情况，这些都是可能在多层嵌套时爆炸的隐患。不可变对象天下第一！

三、找BUG策略

对于自己的程序和自己写的程序（是的这两个概念的外延并不相等），设计过程中会注意到许多坑点，可以针对这些坑点构造测试集。对于别人的程序，因为懒得搞对拍器，我采取的是读代码+手动测试。造测试集时应至少保证覆盖到程序中的每句话和指导书输入规范中的每句话，并适当进行边界情况检验。

四、应用对象创建模式

后两次作业中我采用的递归下降写法极其面向过程，能够改写为工厂模式，用工厂类的子类分别实现各种表达式的解析。