【总结】排序算法

排序

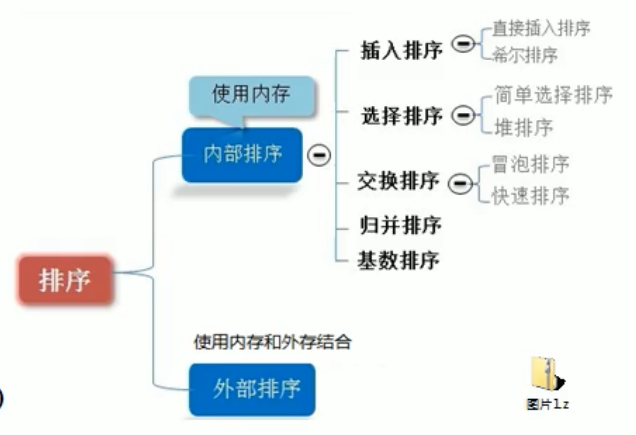
选择排序、快速排序、希尔排序、堆排序不是稳定的排序算法，而冒泡排序、插入排序、归并排序和基数排序是稳定的排序算法
（稳定的排序是指排序前后相同的两个数的相对位置是一致的）

一.冒泡排序 O(N2)

1.算法描述
比较相邻元素，如果第一个比第二个大，交换位置，这样每经过一趟就冒出一个最大的

2.代码实现

        public static int[] bubbleSort(int arr[]) {
        int len = arr.length;
        for (int i = 0; i < len; i++) {
            for (int j = 0; j < len - i - 1; j++) {
                if (arr[j] > arr[j + 1]) {
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
        return arr;
    }

3.优化
（1）如果一趟比较没有任何位置交换，说明它们已经有序，不用再继续下去了。可以设置一个标志位

public static void sort(int[] a) {
        int len = a.length;
        for (int i = 0; i < len; i++) {
            boolean flag = true;
            for (int j = 0; j < len - i - 1; j++) {
                if (a[j] > a[j + 1]) {
                    flag = false;
                    int temp = a[j];
                    a[j] = a[j + 1];
                    a[j + 1] = temp;
                }
            }
            if (flag) {
                return;
            }
        }
    }

（2）最后一次交换位置后面的元素其实已经有序，下次不需要再比较

    public static void sort(int[] a) {
        int len = a.length;
        int k= a.length;
        for (int i = 0; i < len; i++) {
            boolean flag = true;
            int pos = 0;//记录最后一次交换的位置
            for (int j = 0; j < k; j++) {
                if (a[j] > a[j + 1]) {
                    flag = false;
                    pos = j;
                    int temp = a[j];
                    a[j] = a[j + 1];
                    a[j + 1] = temp;
                }
            }
            if (flag) {
                return;
            }
            k = pos;
        }
    }

二.快速排序（nlog2N）

1.算法描述
（1）从数列中挑出一个元素，称为"基准"（pivot）
（2）从左向右找比这个第一个比这个基准大的数，从右往左找第一个比这个基准小的数，找到后互换位置
（3）继续在此基础上执行第二步，直到两个寻找指针相遇，将该位置的数与基准值互换
（4）递归的（recursive）把小于基准值的序列和大于基准值的序列排序

2.代码实现

 public static void quickSort(int[]arr, int left,int right) {
        if(left>right){return; }//递归的出口
        int i = left,j = right;
        int pivot = arr[left];//找到基准
        while (i < j) {
            //从右向左找第一个比基准值小的数
            while (i < j && arr[j] >= pivot) {
                j--;
            }
            //从左向右找第一个比基准值大的数
            while (i < j && arr[i] <= pivot) {
                i++;
            }

            //两面都找到后互换位置
            if (i < j) {
                int tmp = arr[i];
                arr[i] = arr[j];
                arr[j] = tmp;
            }
        }
        //left=right时于基准值互换
        int tmp = arr[j];
        arr[j] = arr[left];
        arr[left] = tmp;
        //分别递归的调用基准值的左边和右边
        quickSort(arr,left,i-1);
        quickSort(arr,i+1,right);

    }

三.简单选择排序 O(N2)

每次选出一个最小的放在已排好队列的末端

public static void sort(int[] a) {
        for (int i = 0; i < a.length; i++) {
            int min = i;
            for (int j = i; j < a.length; j++) {
                if (a[j] < a[min]) {
                    min = j;
                }
            }
            int temp = a[min];
            a[min] = a[i];
            a[i] = temp;
        }
    }

四.插入排序 O(N2)

每次从无序表中选出第一个元素，插在有序表中的正确位置

public static void sort(int[] a) {
        for (int i = 0; i < a.length-1; i++) {
            for (int j = i; j >= 0 && a[j+1] < a[j]; j--) {
                int temp = a[j+1];
                a[j+1] = a[j];
                a[j] = temp;
            }
        }
    }

五.希尔排序 O(N1.3)

插入排序每次只能将数据移动一位 所以希尔排序先将序列分为几个增量区域来分别的进行插入排序，最后对整个序列进行排序

public class Shell {
    public static void sort(int a[]){
        int N = a.length;
        for (int D=N/2;D>0;D/=2){  //增量函数-每次增量减少一半
            for (int i=D;i<N;i++){
                for (int j=i;j>=D&&a[j]<a[j-D];j-=D){
                    int t = a[j];
                    a[j] = a[j-D];
                    a[j-D] = t;
                }
            }
        }
 
    }
}

六.归并排序 （nlog2N）

归并排序首先将排序数组递归等分切割直到数组中的基本元素（1个元素），然后归并两个这样的基本单元，并逐渐向上层归并，直到回到排序数组左右各一半的情况，此时将进行最后一次归并，而左右子数组均已是有序数组
速度仅次于快速排序，为稳定排序算法

public class Merge {

    private static void sort(int[] a, int left, int right, int[] temp) {
        if (left < right) {
            int mid = (left + right) / 2;
            sort(a, left, mid, temp);
            sort(a, mid + 1, right, temp);
            merge(a, left, mid, right, temp);
        }
    }

    private static void merge(int[] a, int left, int mid, int right, int[] temp) {
        int i = left;//左序列指针
        int j = mid + 1;//右序列指针
        int t = 0;//临时数组指针

        while (i <= mid && j <= right) {
            if (a[i] < a[j]) {
                temp[t++] = a[i++];
            } else {
                temp[t++] = a[j++];
            }
        }
        while (i <= mid) {
            temp[t++] = a[i++];
        }
        while (j <= right) {
            temp[t++] = a[j++];
        }
        //将结果拷贝到原数组
        t = 0;
        while (left <= right) {
            a[left++] = temp[t++];
        }
    }
}