【总结】树

一.二叉树

1.满二叉树

高度为h，由2的h次-1个节点构成的二叉树称为满二叉树

2.完全二叉树

高度为h，除第h层外，其它各层节点数都到达最大节点数。且第h层的节点都连续集中在最左边

二.二叉查找树

又称二叉排序树或二叉搜索树。左子树的所有节点值均小于根节点的值，右子树所有节点值均大于根节点的值。且左右子树也分别为二叉排序树。
1.插入操作
（1） 若当前的二叉查找树为空，则插入的元素为根节点
（2） 若插入的元素值小于根节点值，则将元素插入到左子树中
（3） 若插入的元素值不小于根节点值，则将元素插入到右子树中

class Node {
    int key;
    int value;
    Node leftChild;
    Node rightChild;

    public Node(int key, int value) {
        this.key = key;
        this.value = value;
    }

}

public void insert(int key, int value) {
        if (root == null) {
            root = new Node(key, value);
            return;
        }
        Node currentNode = root;
        Node parentNode = root;
        boolean isLeftChild = true;
        while (currentNode != null) {
            parentNode = currentNode;
            if (key < currentNode.key) {
                currentNode = currentNode.leftChild;
                isLeftChild = true;
            } else {
                currentNode = currentNode.rightChild;
                isLeftChild = false;
            }
        }
        Node newNode = new Node(key, value);
        if (isLeftChild) {
            parentNode.leftChild = newNode;
        } else {
            parentNode.rightChild = newNode;
        }
}

2.查找操作

public Node find(int key) {
        Node currentNode = root;
        while (currentNode != null && currentNode.key != key) {
            if (key < currentNode.key) {
                currentNode = currentNode.leftChild;
            } else {
                currentNode = currentNode.rightChild;
            }
        }
        return currentNode;
}

三.平衡二叉树

对于一颗二叉查找树，其期望高度是log2n（树平衡时），时间复杂度o（log2n）。但是在某些极端情况下，如插入时的序列是有序时，这时将退化成一条链，这时将退化为线性，复杂度将变为n。于是就有了平衡二叉树。

平衡二叉树：左右两个子树的高度差绝对值不超过1.并且左右两个子树都是平衡二叉树。平衡二叉树的常用算法有红黑树、AVL树等。

1.平衡二叉树之AVL树

AVL树得名于它的发明者 G.M. Adelson-Velsky。左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。查找、插入和删除在平均和最坏情况下都是O(logn)。

2.平衡二叉树之红黑树

从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。

3.AVL和红黑树的区别

（1）红黑树放弃了追求完全平衡，追求大致平衡，保证每次插入最多只需要三次旋转就能达到平衡，实现起来也更为简单
（2）平衡二叉树追求绝对平衡，条件比较苛刻，旋转的次数无法预知
（3）如果是增删操作多的话，用红黑树。如果是查询操作多的话，用avl树

四.多路平衡查找树

树深度过大而造成磁盘IO读写过于频繁，进而导致效率低下。所以需要降低查找树的高度。出现了多路平衡查找树

1.B树

1.基本概念
（1）阶：结点的分支数等于关键字数+1，最大的分支数就是B-树的阶数，通常用m表示（比如最多关键字4个，它有5个分支，阶数为5）
（2）根结点至少有两个子女
（3）每个中间节点都包含k-1个元素和k个孩子，其中 m/2 <= k <= m
（4）所有的叶子结点都位于同一层。
（5）每个节点中的元素从小到大排列

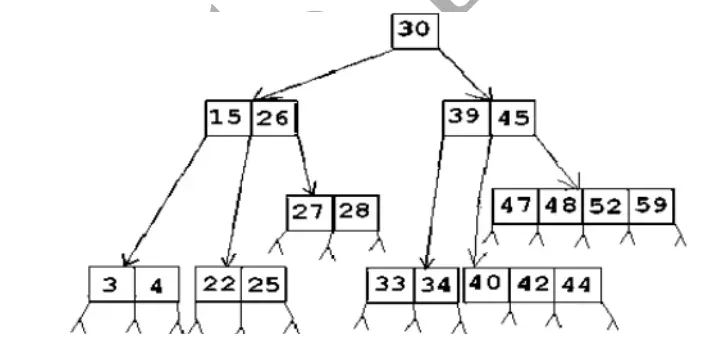
（如图：该树为5阶树）

2.B+树

1.基本概念
（1）有k个子树的中间节点包含有k个元素（B树中是k-1个元素），每个元素不保存数据，只用来索引，所有数据都保存在叶子节点。
（2）所有的叶子结点中包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。
（3）所有的中间节点元素都同时存在于子节点

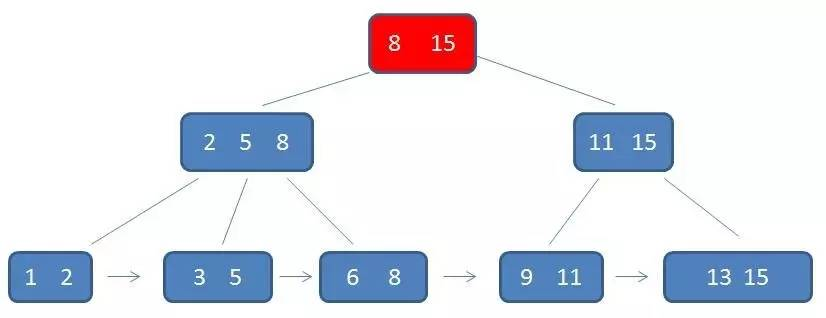
2.B+树相对于B树的优势
（1）单一节点存储更多的元素（中间节点不存储数据，值存储索引，所以同样的磁盘页可以容纳更多的节点元素），使得查询的IO次数更少。
（2）所有查询都要查找到叶子节点，查询性能稳定。
（3）所有叶子节点形成有序链表，便于范围查询。