python之二叉树
可以使用以下函数创建并操作二叉树
- BinaryTree()创建一个二叉树实例。
- getLeftChild()返回当前节点的左子节点所对应的二叉树。
- getRightChild()返回当前节点的右子节点所对应的二叉树。
- setRootVal(val)在当前节点中存在存储参数val中的对象。
- getRootVal()返回当前节点存储的对象。
- insertLeft(val)新建一棵二叉树,并将其作为当前节点的左子节点。
- insertRight(val)新建一棵二叉树,并将其作为当前节点的右子节点。
实现树的关键在于选择一个好的内部存储技巧。python提供两种有意思的方式,我们再选择前会仔细了解这两种方式。第一种称作为“列表之列表”,第二种称作“节点与引用”。
1.1、列表之列表
用“列表之列表”表示树时,先从python的列表数据结构开始,编写前面定义的函数。尽管为列表编写一套操作的接口与已经现实的其他抽象数据类型有些不同,但是做起来很有意思,因为这会给我们提供一个简单的递归数据类型,供我们直接查看和检查。在“列表之列表”的树中,我们将根节点的值作为列表的第一个元素;第二个元素是代表左子树的列表;第三个元素是代表右子树的列表。要理解这个存储技巧,来看一个例子,下图展示一棵简单的树及其对应的列表实现。
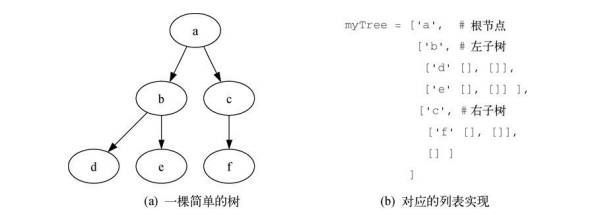
注意,可以通过标注的列表切片操作访问子树。树的根节点myTree[0],左子树是myTree[1],右子树是myTree[2]。以下会展示了如何使用列表创建树。一旦创建完成,就可以访问它的根节点、左子树和右子树。“列表之列表”表示法有个很好的性质,那就是表示子树的列表结构符合树的定义,这样的结构是递归的!由一个根节点和两个空列表结构的子树是一个叶子节点。还有一个很好的性质,那就是这种表示法可以推广到有很多子树的情况。如果树不是二叉树,则多一个子树只是多一个列表。
接下来提供一些便于将列表称作树使用的函数,以正式定义树的数据结构。注意,我们不是要定义二叉树类,而是要创建可用于标准列表的函数。
def BinartyTree(r): return [r, [], []]
Binarytree函数构造一个简单的列表,它仅有一个根节点和两个作为子节点的空列表,要给树添加左子树,需要在列表的第二个位置加入一个新列表。请务必当心:如果列表的第二个位置上已经有内容了,我们要保留已有内容,并将它作为新列表的左子树。一下给出了插入左子树的python代码。
def insertLeft(root,newBranch): t = root.pop(1) if len(t) > 1: root.insert(1, [newBranch, t, []]) else: root.insert(1, [newBranch, [], []]) return root
在插入左子树时,先获取当前的左子树所对应的列表(可能为空),然后加入新的左子树,将旧的左子树作为新节点的左子树。这样一来,就可以在树的任意位置插入新节点。insertRight与insertLeft类似,代码如下。
def insertRight(root,newBranch): t = root.pop(2) if len(t) > 1: root.insert(2, [newBranch, [], t]) else: root.insert(2, [newBranch, [], []]) return root
为了完整地创建树的函数集,让我们来编写一些访问数据,用于读写根节点与左右子树,如下代码所示。
def getRootVal(root): return root[0] def setRootVal(root, newval): root[0] = newval def getLeftChild(root): return root[1] def getRightChild(root): return root[2]
1.2、节点与引用
树的第二种表示法是利用节点与引用。我们将定义一个类,其中有根节点和左右子树的属性。这种表示法遵循面向对象编程范式,所以本章后续内容会采用这种表示方法。
采用“节点与引用”表示法时,可以将树想象成如图所示结构
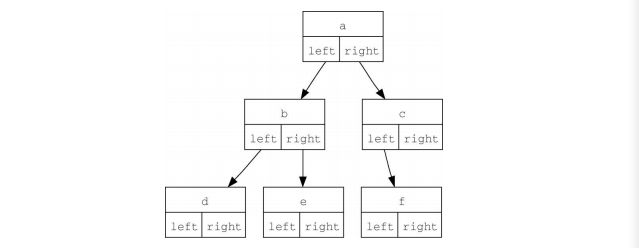
首先定义一个简单的类,如下代码所示。“节点与引用”表示法的要点是,属性left和right会指向BinaryTree类的其他实例。举例来说,在向树中插入新的左子树时,我们会创建另一个BinaryTree实例,并将根节点的self.leftChild改为指向新树。
class BinaryTree: def __init__(self,rootObj): self.key = rootObj self.leftChild = None self.rightChild = None
在上面代码清单中,构造方法接受一个对象,并将其存储到根节点中。正如能在列表中存储任何对象,根节点对象也可以成为任何对象的引用。就之前的例子而言,我们将节点名作为根节点的值存储。采用“节点与引用”法表示图中的树。
下面将看看基于根节点构建树所需要的函数。为了给树添加左子树,我们新建一个二叉树对象,将根节点的left属性指向新对象。以下代码给出了insertLeft函数的代码。
def insertLeft(self,newNode): if self.leftChild == None: self.leftChild = BinaryTree(newNode) else: t = BinaryTree(newNode) t.leftChild = self.leftChild print(t.left) self.leftChild = t
在插入左子树时,必须考虑两种情况。第一种情况是没有左子节点。此时,只需要往树中添加一个节点即可。第二种情况是已经存在左子节点。此时,插入一个节点,并将已有的左子节点降一层。上面代码中的else语句处理的就是第二种情况。
def insertRight(self,newNode): if self.rightChild == None: self.rightChild = BinaryTree(newNode) else: t = BinaryTree(newNode) t.rightChild = self.rightChild self.rightChild = t
def getRightChild(self): return self.rightChild def getLeftChild(self): return self.leftChild def setRootVal(self,obj): self.key = obj def getRootVal(self): return self.key



 浙公网安备 33010602011771号
浙公网安备 33010602011771号