手搓数据结构与算法 day1 树的概念

基本概念

• 节点：使用树结构存储的每一个数据元素都被称为“结点”。
• 节点度：有一个特殊的结点，这个结点没有前驱，我们将这种结点称之为根结点
• 叶子：：如果一个结点没有任何子结点，那么此结点就称之为叶子结点。
• 树的度：书中各个节点度的最大值
• 节点的关系：根节点，父节点，子节点，孙子节点，兄弟节点，叔叔节点
• 树的深度或者高度：结点的层次从根结点开始定义起，根为第一层，根的孩子为第二层。依次类推

例子

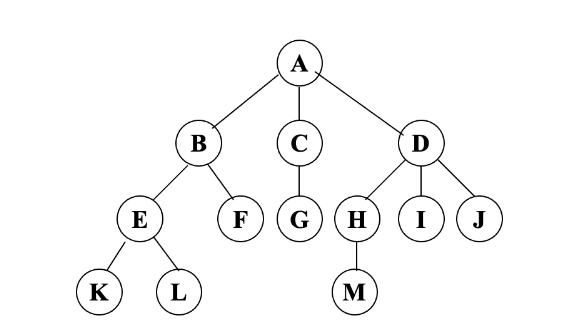
树的存储结构（了解即可）

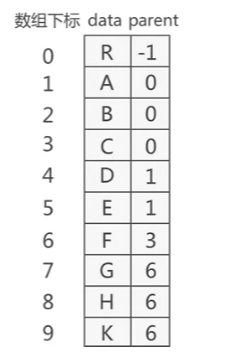
双亲表示法

双亲表示法采用顺序表（也就是数组）存储普通树，其实现的核心思想是：顺序存储各个节点的同时，给各节点附加一个记录其父节点位置的变量
根节点没有父节点（父节点又称为双亲节点），因此根节点记录父节点位置的变量通常置为 -1

• 利用顺序表存储，表元素由数据和父结点构成
• 特点分析：
  • 根结点没有双亲，所以位置域设置为-1
  • 知道一个结点，找他的父结点，非常容易，O(1)级
  • 找孩子节点，必须遍历整个表

例子

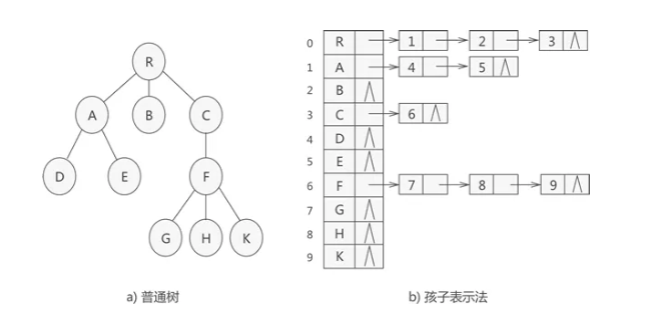
孩子表示法

• 孩子表示法存储普通树采用的是顺序表+链表的组合结构。
• 其存储过程是：从树的根节点开始，使用顺序表依次存储树中各个节点。需要注意，与双亲表示法不同的是，孩子表示法会给各个节点配备一个链表，用于存储各节点的孩子节点位于顺序表中的位置
• 如果节点没有孩子节点，则该节点链表为空链表

例子

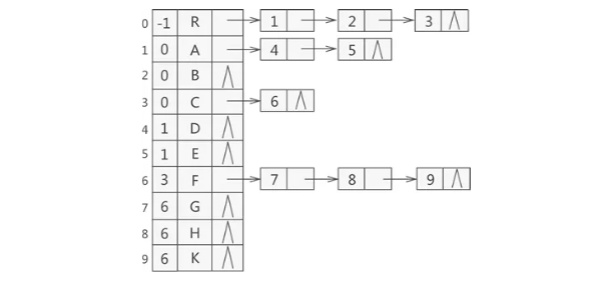
改进

• 使用孩子表示法存储的树结构，正好和双亲表示法相反，查找孩子结点的效率很高，而不擅⻓做查
  找父结点的操作。
• 我们还可以将双亲表示法和孩子表示法合二为一：

孩子兄弟表示法

• 所谓孩子兄弟表示法，指的是用将整棵树用二叉链表存储起来，具体实现方案是：从树的根节点开
  始，依次存储各个结点的孩子结点和兄弟结点
• 在二叉链表中，各个结点包含三部分内容，孩子指针域，数据域，兄弟指针域

例子

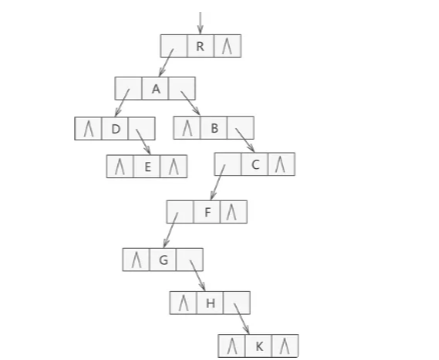
重构方法

在以孩子兄弟表示法构建的二叉链表中，如果要查找结点 x 的所有孩子，则只要根据该结点的 firstchild 指针找到它的第一个孩子，然后沿着孩子结点的 nextsibling 指针不断地找它的兄弟结点，就
可以找到结点 x 的所有孩子。