2022牛客暑期多校第四场
【思维】N
【题意】
给 n 个整数,每次随机选择其中两个整数 a,b,将其替换为 a AND b 和 a OR b(位运算),直到稳定,求最终稳定状态的方差,输出最简分数形式。$2 \leq n \leq 10^5, 1 \leq a_i \leq 2^{15}$
【题解】
通过位运算表不难发现,替换之后相当于把 a 和 b 的二进制各个位上的 1 都尽量集中到一个数上,那么最终的稳定状态就是把所有数的二进制的各个位上的 1 都尽量集中起来。比如:
0 0 1 0 0 1 0 0 0 0 0 0
1 0 1 1 1 0 -> 0 0 1 1 0 1
0 1 0 1 0 1 1 1 1 1 1 1
算方差时用$Var(X) = E(X^2) - E(X)^2 = \frac{n\sum X^2 - (\sum X)^2}{n^2}$得到整数分子分母。由于每一位上 1 的个数不变,数的个数也不变,$\sum x$不变。
【代码】
#include <bits/stdc++.h> using namespace std; const int N=1e5+5; int n,cnt[20]; long long t,sum,mx,res; void solve(long long x){ // 统计每一位上共有几个1 int len=1; while (x){ cnt[len]+=x%2; len++; x/=2; } } long long Pow(long long x,int y){ long long res=1ll; while (y){ if (y&1) res*=x; x*=x; y>>=1; } return res; } long long gcd(long long x,long long y){ return y==0?x:gcd(y,x%y); } int main() { scanf("%d",&n); for (int i=1;i<=n;i++){ scanf("%lld",&t); solve(t); sum+=t; } for (int i=1;i<=n;i++){ t=0ll; for (int j=15;j>=1;j--){ //最终稳定状态下的数 if (cnt[j]) t+=Pow(2ll,(long long)j-1ll),cnt[j]--; } res+=t*t; //sum(X^2) } sum*=sum; //sum(X)^2 res*=(long long)n; //n*sum(X^2) long long g=gcd(res-sum,(long long)n*(long long)n); printf("%lld/%lld",(res-sum)/g,(long long)n*(long long)n/g); return 0; }
【思维】K
【题意】
按顺序击杀 1 到 n 只怪,击杀第 i 只怪要求$A \equiv i\ (mod\ n)$,其中 A 的初值为 0,任意时刻可以对 A 进行任意次数的如下操作:选择一个整数$x \in [0,9]$,$A = 10A + x$。求最少操作几次。$1 \leq n \leq 10^6$
【题解】
假设当前值为 A,进行一次操作后$A \in [10A,10A+9]$。如果区间长度大于等于 n,则必然存在一个 x,使得同余式成立。如果区间长度小于 n,只需判断 i%n 是否被包含在内。对于新的 i,从小到大枚举操作次数即可。发现跑得很快,因此时间复杂度正确。
【代码】
#include <bits/stdc++.h> using namespace std; long long n,ans,l,r; int main() { scanf("%lld",&n); for (long long i=1;i<=n;i++){ l=i-1; r=i-1; while (1){ ans++; l=l*10; r=r*10+9; //进行一次操作后的区间 if (r-l+1>=n) break; if (l%n<=r%n&&l%n<=i%n&&r%n>=i%n) break; // 0 --- l%n ———— r%n --- n-1 的情况 if (l%n>r%n&&(l%n<=i%n||r%n>=i%n)) break; // 0 ———— r%n --- l%n ———— n-1 的情况 } } if (n!=1) printf("%lld",ans); else printf("0"); return 0; }
【构造+贪心】H
【题意】
给定一个整数 n,有 n 块 1x1,n-1 块 1x2,...,2 块 1x(n-1),1 块 1xn 的木板,求如何把他们拼成一个长方形,使得周长最小。输出每块木板左下角和右上角的坐标。$1 \leq T \leq 100, 1 \leq n \leq 100$
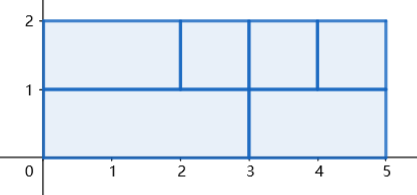
【题解】
解决边长:面积一定,越接近正方形周长约小,因此将最接近$\sqrt{S}$的一对因数作为边长,其中 S 为木板总面积。
解决怎么拼:贪心,每次选当前层放得下的最长的木板。经过验证发现可行。
【实现】
解决边长:将大的因数作为每层的长度,小的作为层的数量,因为小的有可能小于 n,即最长的木板的长度。
解决怎么拼:可以用 lower_bound 查找,添加 greater<int>()在单减序列中查找第一个小于等于目标的数,注意范围上界是 min(当前层剩余长度,n)
【代码】
#include <bits/stdc++.h> using namespace std; int T,n,cnt[105],flag[105],sum,a,ans[105][105][4],cur; int find(int x){ //返回边长 int b=(int)sqrt((double)x)+1; for (int i=b;i>=1;i--){ if (x%i==0) return max(x/i,i); //取较大的作为层宽 } } void solve(){ sum=0; //总面积 for (int i=1;i<=n;i++){ cnt[i]=n-i+1; //cnt[i]表示长度为i的木板还剩几个 flag[i]=1; //flag[i]表示长度为i的木板是否有剩余 sum+=cnt[i]*i; } a=find(sum); printf("%d\n",2*(a+sum/a)); for (int i=1;i<=sum/a;i++){ cur=0; while (cur<a){ int len=lower_bound(flag+1,flag+min(a-cur,n)+1,0,greater<int>())-flag-1; //查找当前层放得下的最长的木板 cnt[len]--; if (cnt[len]==0) flag[len]=0; int id=(n-len+1)-cnt[len]; //木板编号 ans[len][id][0]=cur; ans[len][id][1]=i-1; ans[len][id][2]=cur+len; ans[len][id][3]=i; cur+=len; } } } int main() { scanf("%d",&T); while (T--){ scanf("%d",&n); solve(); for (int i=1;i<=n;i++) for (int j=1;j<=(n-i+1);j++) printf("%d %d %d %d\n",ans[i][j][0],ans[i][j][1],ans[i][j][2],ans[i][j][3]); } return 0; }
【三维前缀或】D
【题意】
有 n 个公司,每个公司有 mi 份工作,每份工作对 IQ,EQ,AQ 有最低门槛,满足同一家公司的任意一份工作的要求就可以去这家公司。q 次询问,每次给一个人的三商,问他能去几家公司,强制在线。$1 \leq n \leq 10, 1 \leq m_i \leq 10^5, 1 \leq IQ,EQ,AQ \leq 400, 1 \leq q \leq 2 \times 10^6$,时限3s。
【题解】
超大询问次数+强制在线+范围较小的值(400),考虑预处理。
如果第 i 家公司存在三商最低门槛为 x,y,z 的工作,则 a[x][y][z] 的二进制第 i 位为 1。对 a 维护三维前缀或(或运算不用容斥),对于询问 x,y,z,答案即为 sum[x][y][z] 的二进制表示中有多少 1。
【代码】
#include <bits/stdc++.h> #include <random> using namespace std; const long long mod=998244353; int lastans=0,n,q,m,seed,sum[405][405][405],a,b,c; long long ans; long long Pow(long long x,long long y){ long long res=1ll; x%=mod; while (y){ if (y&1) res=res*x%mod; x=x*x%mod; y>>=1; } return res; } int solve(int x,int y,int z){ int res=0,tmp=sum[x][y][z]; while (tmp){ if (tmp&1) res++; tmp>>=1; } return res; } int main() { scanf("%d%d",&n,&q); for (int i=1;i<=n;i++){ scanf("%d",&m); for (int j=1;j<=m;j++){ scanf("%d%d%d",&a,&b,&c); sum[a][b][c]|=(1<<(i-1)); } } for (int i=1;i<=400;i++) for (int j=1;j<=400;j++) for (int k=1;k<=400;k++) sum[i][j][k]=sum[i][j][k]|sum[i-1][j][k]|sum[i][j-1][k]|sum[i][j][k-1]; scanf("%d",&seed); std::mt19937 rng(seed); //这两行必须放在主函数里 std::uniform_int_distribution<> u(1,400); for (int i=1;i<=q;i++){ int IQ=(u(rng)^lastans)%400+1; // The IQ of the i-th friend int EQ=(u(rng)^lastans)%400+1; // The EQ of the i-th friend int AQ=(u(rng)^lastans)%400+1; // The AQ of the i-th friend lastans=solve(IQ,EQ,AQ); // The answer to the i-th friend ans=(ans+1ll*lastans*Pow(1ll*seed,1ll*(q-i))%mod)%mod; //printf("qwq %d %d %d %d %lld\n",IQ,EQ,AQ,lastans,ans); } printf("%lld",ans); return 0; }
【偏序分析+线性dp】A
【题意】
有 n 台电脑,每台有两个属性 wi 和 pi,从中选 m 台并将它们排序,使得效率$\sum_{i=1}^{m} w_i \prod_{j=1}^{i-1} p_j$最大。$1 \leq n \leq 10^5, 1 \leq m \leq min(n,20)$
【题解】
首先解决顺序问题。对于序列中相邻的两台电脑 a 和 b,a 排在 b 前的效率为${prefix\ part} + w_a \prod p_{prefix} + w_b (\prod p_{prefix})p_a + {suffix\ part}$,b 排在 a 前的效率为${prefix\ part} + w_b \prod p_{prefix} + w_a (\prod p_{prefix})p_b + {suffix\ part}$,则 ab 比 ba 效率高须满足$w_b + w_a p_b > w_b + w_a p_b$,此条件符合偏序性质,因此可以据此对 n 台电脑排序。
dp[i][j] 表示考虑了第 i ~ n 台电脑,选择了 j 台时的最大效率,则 dp[i][j] = max(选第 i 台,不选第 i 台) = max(dp[i+1][j], dp[i+1][j-1] * p[i] + w[i])。初始状态为 dp[i][0] = 0,所求答案为 dp[1][m]。
【代码】
#include <bits/stdc++.h> using namespace std; int n,m; double dp[100005][25]; struct node{ double w,q; }a[100005]; bool cmp(node A,node B){ return A.w*10000+A.q*B.w>B.w*10000+B.q*A.w; } int main() { scanf("%d%d",&n,&m); for (int i=1;i<=n;i++) scanf("%lf",&a[i].w); for (int i=1;i<=n;i++) scanf("%lf",&a[i].q); sort(a+1,a+n+1,cmp); for (int i=n;i>=1;i--) for (int j=0;j<=m;j++){ if (j==0) dp[i][j]=dp[i+1][j]; else dp[i][j]=max(dp[i+1][j],dp[i+1][j-1]*a[i].q/10000+a[i].w); } printf("%.15lf",dp[1][m]); return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号