2022牛客暑期多校第一场
【几何】D
【题意】
给定一个以原点 O 为圆心,半径为 r 的圆,和一个在圆内的点 Q(x,y)。以 Q 为中点,作一条长为 2d 的线段 AB,方向不限(即 AB 可以绕 Q 旋转),数据保证 AB 始终在圆内。求 AB 对应的圆弧最长是多少。
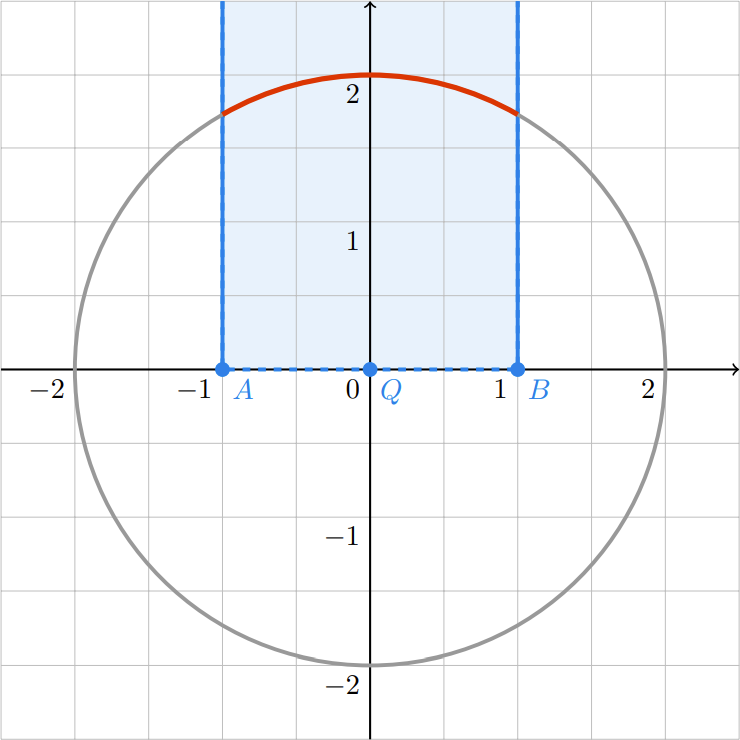
【题解】
结论就是(不难推测)当 AB 与 OQ 重合时对应的圆弧最长,可以依此用计算几何算。证明/更简单的计算方法如下:根据圆的对称性,可以将任意位置任意方向的 AB 都转移到 x 轴上,如图,
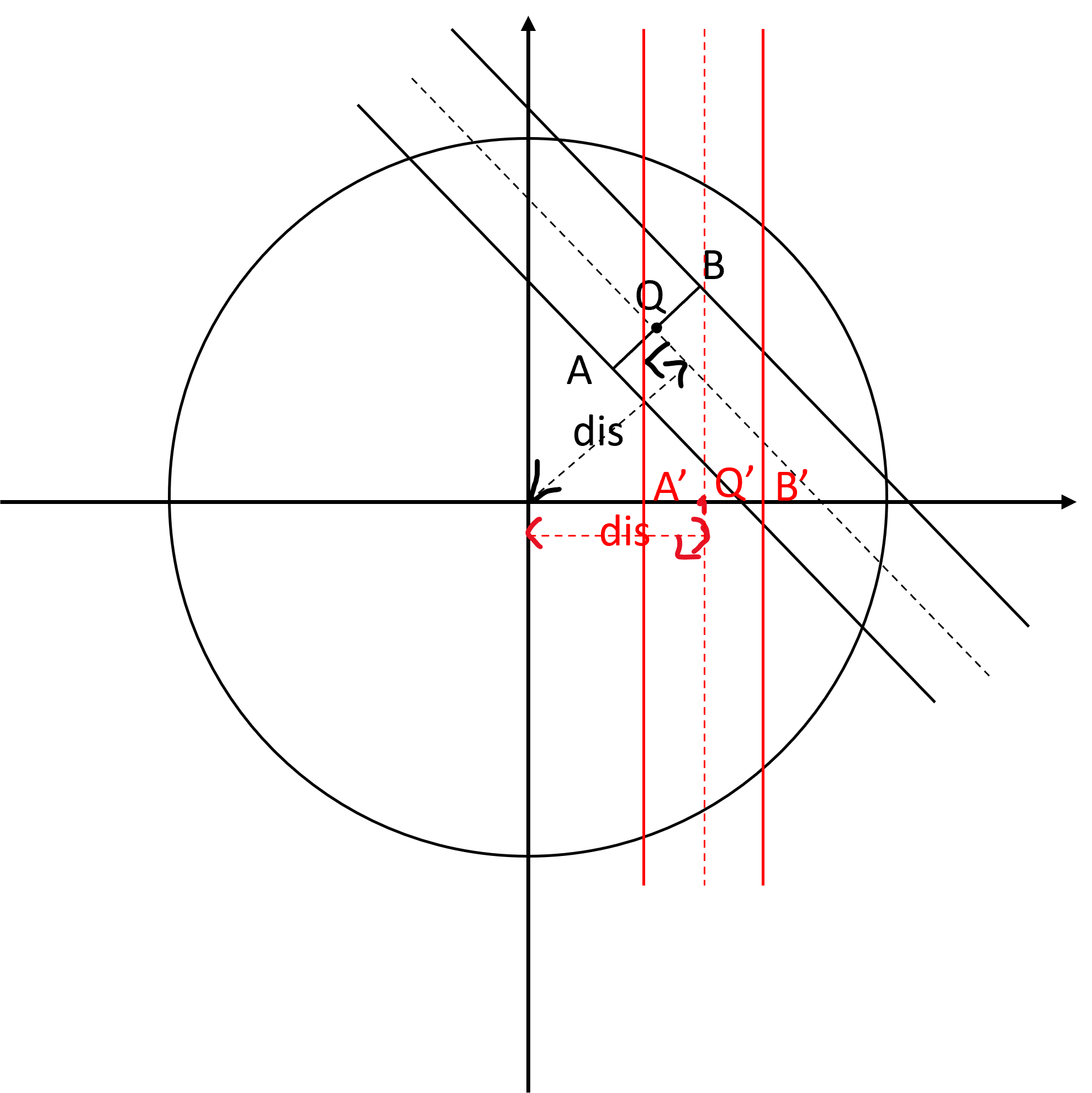
因此问题转化成在 x 轴上左右滑动 AB(不超出圆),使得对应的圆弧最长。可以很直观地观察到,在长度固定的情况下,圆弧越陡越长。因此 AB 最靠近圆边界,即 dis 最长,dis=OQ,AB 与 OQ 重合时,圆弧最长。
【实现】
比赛时用计算几何写的,涉及到判断两条平行线与圆相交的4个交点中,哪2个所夹圆弧是所求圆弧的问题。解决方法之一是比较各个交点到 A/B 的向量。但注意不要比较大小(归一化之后),会有精度损失。比较方向即可,注意方向相同是相乘>=0。
【观察+实现】C
【题意】
y 轴上从 (0,1) 到 (0,m) 是屏幕,屏幕右侧横坐标范围 [1,n],纵坐标范围 [1,m] 的整点是座位。有 k 个人已经占了座, 问还有几个空座位可以完整地看到屏幕。有 q 次询问,每次询问更改一个人的位置。$2 \leq n,m \leq 2 \times 10^5, 1 \leq k \leq 2 \times 10^5, 1 \leq q \leq 200$,时限5s。
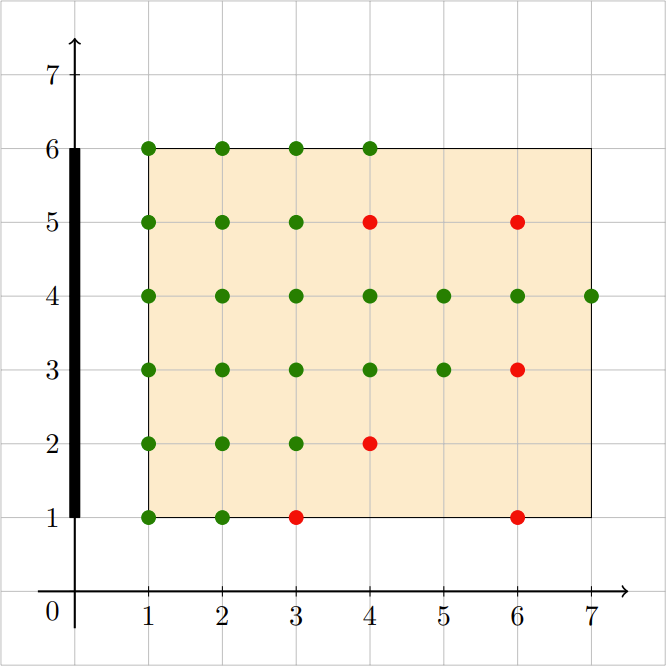
【题解】
对于每一个有人的座位(红点),它遮挡的区域的边界是屏幕的两个端点和这个点的连线:
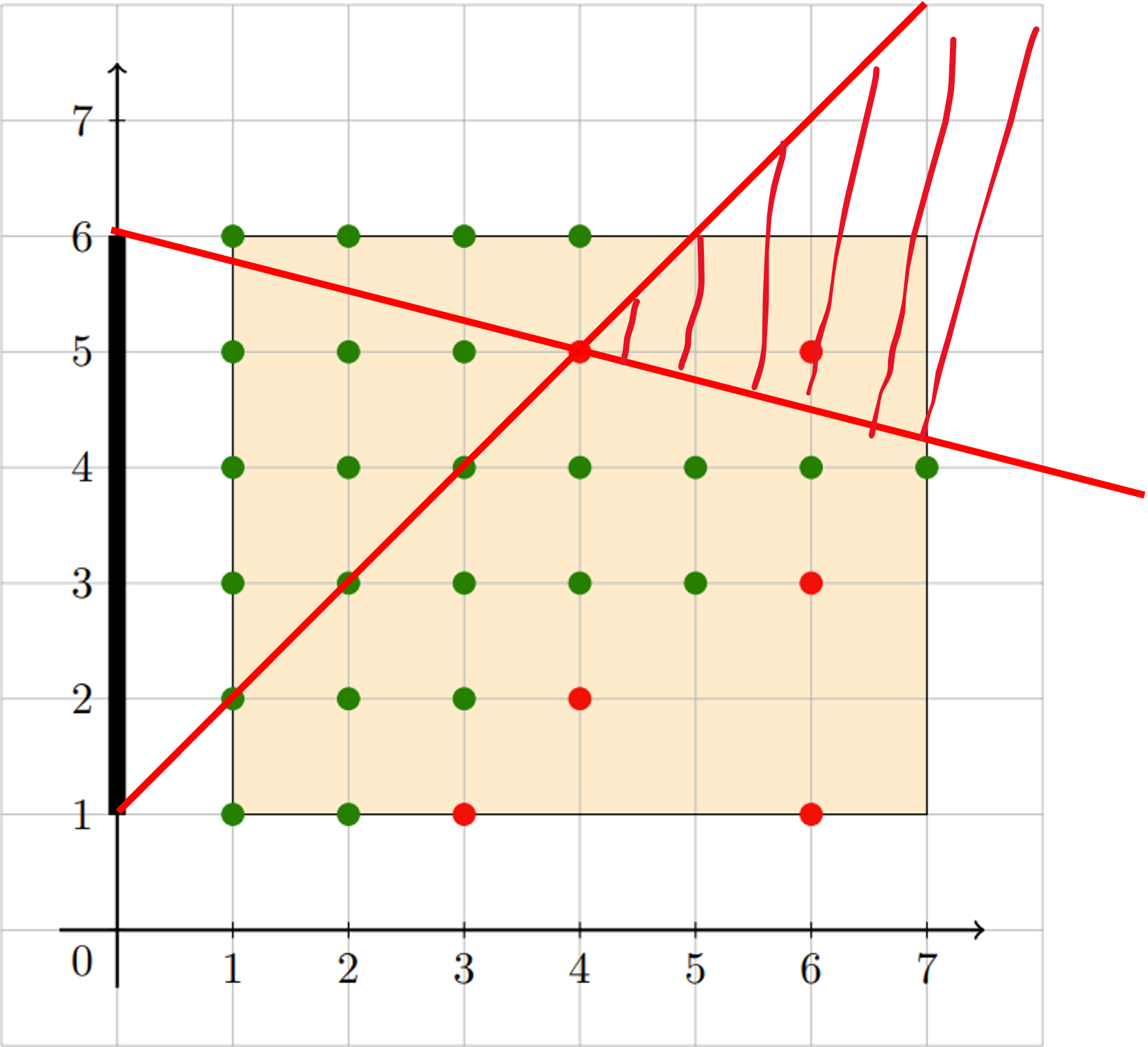
可以注意到同一行上的点,靠右的点遮挡的区域总是靠左的点遮挡的区域的子集,因此只需考虑每一行最左边的点。屏幕下端点 (0,1) 与某个点的连线,只可能遮挡行数>=该点的点,且斜率大的线遮挡的范围更大。因此处理方法是:对于 (0,1) 发出的射线,从下往上遍历每行最左边的点,维护当前最大斜率,更新每行能看见屏幕的座位数;对于 (0,m) 发出的射线,从上往下遍历,维护当前最小/绝对值最大的斜率,更新每行能看见屏幕的座位数。时间复杂度$O(qm)$。
【实现】
ceil() 函数卡精度。
下取整:(int)(x - eps)
上取整:(int)(x - eps) + 1
eps = 1e-9
【代码】
#include <bits/stdc++.h> using namespace std; const int N=2e5+5; const double EPS=1e-9; int n,m,K,q,a[N][2],p,leftmost[N],res[N]; //a: 点的坐标; leftmost[i]: 第i行最靠左的不合法的; res[i]: 第i行最靠右的合法的 double mxk,curk; long long ans; int main() { scanf("%d%d%d%d",&n,&m,&K,&q); for (int i=1;i<=K;i++) scanf("%d%d",&a[i][0],&a[i][1]); while(q--){ scanf("%d",&p); scanf("%d%d",&a[p][0],&a[p][1]); for (int i=1;i<=m;i++) leftmost[i]=n+1,res[i]=n; for (int i=1;i<=K;i++) //更新最靠左的有人的位置 leftmost[a[i][1]]=min(leftmost[a[i][1]],a[i][0]); ans=0ll; mxk=0.0; for (int i=1;i<=m;i++){ curk=(double)(i-1)/(double)leftmost[i]; if (curk>mxk) mxk=curk; if (mxk>0.0) res[i]=min(res[i],(int)((double)(i-1)/mxk - EPS)); //if判断,避免除0 } mxk=0.0; for (int i=m;i>=1;i--){ curk=(double)(m-i)/(double)leftmost[i]; //m-i取负 if (curk>mxk) mxk=curk; if (mxk>0.0) res[i]=min(res[i],(int)((double)(m-i)/mxk - EPS)); ans+=(long long)res[i]; } printf("%lld\n",ans); } return 0; }
【期望dp】I
【题意】
一副牌,34种牌面,每种4张。拥有7个对子时胡牌。初始手牌13张,保证每种不超过2张。每轮从牌堆中摸一张牌,判断是否胡牌,胡牌就终止,否则弃一张牌,弃牌不放回牌堆,开始下一轮。求最佳策略下胡牌所需轮数的期望。
【题解】
比较绕弯弯。
首先考虑最佳策略。每次摸牌会出现三种情况:
- 摸到已有一对的牌:弃该张牌,因为已经有一对了,单牌数量不变
- 摸到没有的牌:需要弃一张单牌,单牌数量不变
- 摸到只有一张的牌:弃手牌中的一张单牌,单牌数量-2
对于情况2,不妨就弃摸到的牌,这样可以保证对于手中的单牌,牌堆中总是剩余3张。这种策略是不劣的,因此是最优的。
然后考虑 dp。设 dp[i][j] 表示牌堆中还剩 i 张牌,手牌中还有 j 张单牌时,胡牌所需轮数的期望。根据以上策略,dp 转移式为:
$$ dp[i][j]=\left\{\begin{matrix}
1 + \frac{i-3j}{i}dp[i-1][j],\ j=1 \\
1 + \frac{i-3j}{i}dp[i-1][j] + \frac{3j}{i}dp[i-1][j-2],\ j>1\end{matrix}\right. $$
“+1”表示当前轮,$\frac{i-3j}{j}dp[i-1][j]$为情况1和情况2,$\frac{3j}{i}dp[i-1][j-2]$为情况3。
初始状态为 dp[3][1] = 1,所求答案为 dp[34*4-13=123][s0],s0 表示初始手牌中的单牌数。
【实现】
It can be shown that the answer can be represented as a fraction $p/q$, where $p$ and $q$ are both positive integers and coprime. If there exists a non-negative integer $r$ less than $10^9+7$ satisfying $q \cdot r mod (10^9+7) = p$, we call the integer $r$ the result of $p/q$ module $10^9+7$.
逆元操作。$\div x$变成$\times x^{mod-2}$。
以及记得乘 1ll。
【代码】
#include <bits/stdc++.h> using namespace std; const int mod=1e9+7; int T,s0,p[50],t; long long dp[135][15]; string s; long long Pow(long long a,long long b){ long long res=1ll; // a=a%mod; while (b){ if (b&1) res=res*a%mod; a=a*a%mod; b>>=1; } return res; } void solve(){ dp[3][1]=1ll; for (int i=4;i<=123;i++) for (int j=1;j<=13&&3*j<=i;j++){ dp[i][j]=(1ll+1ll*3*j*Pow(1ll*i,1ll*(mod-2))%mod*dp[i-1][max(j-2,0)]%mod+1ll*(i-3*j)*Pow(1ll*i,1ll*mod-2ll)%mod*dp[i-1][j]%mod)%mod; // //printf("dp[%d][%d]=%lld\n",i,j,dp[i][j]); } } int main() { solve(); cin>>T; for (int id=1;id<=T;id++){ cin>>s; memset(p,0,sizeof(p)); for (int i=0;i<s.length();i+=2){ t=s[i]-'0'; if (s[i+1]=='p') t+=10; else if (s[i+1]=='s') t+=20; else if (s[i+1]=='z') t+=30; p[t]++; } s0=0; for (int i=1;i<=37;i++) if (p[i]==1) s0++; printf("Case #%d: %lld\n",id,dp[123][s0]); } return 0; }
【图性质分析+随机化/启发式合并】J
【题意】
有一张$n$点$m$边的无重边无自环的有向图。初始时任选一点染黑。某个白点被染黑,当且仅当其所有入边的起点都被染黑。入度为 0 的点只有在被选择为起始点时才可被染黑。求最多有多少个点被染黑。$1 \leq n \leq 2 \times 10^5, 0 \leq m \leq 5 \times 10^5$,时限2s。
【题解】
首先,对图的性质进行分析,$S_i$表示以$i$为起始点,染黑的点的集合,可以得出一下性质:
- 如果$v \in S_u$,则$S_v \subseteq S_u$
- 如果$S_u \cap S_v \neq \varnothing$,则$S_v \subseteq S_u$或$S_u \subseteq S_v$
性质1显然成立,性质2证明如下:

因此,每个$S_i$形成一棵树,不同树之间要么不交,要么包含,最终形成一个森林。森林中最大的树就是答案。
对于如何寻找这颗最大的树,有两种方法:随机化或启发式合并。
—随机化—
以随机排列$p$遍历所有点,第$i$个被遍历的点为$p_i$,当且仅当$p_i \notin S_{p1} \cap S_{p2} \cap \cdots \cap S_{pi-1}$ ,即$p_i$没有被访问过时,由$p_i$开始搜索整个$S_{pi}$。如此,最大的树必然被搜索到。
该算法的期望时间复杂度为$O(mlogn)$,证明如下:
对于任意点$u$,考虑其出边被访问的期望次数。设$u$的出边在其所属的最大树中深度为$x$,记其被访问的期望次数为$f(x)$。每次搜索$u$的祖先时$u$的出边都会被访问到,由此可以写出(我没看懂TT,但手推了几个确实是正确的):
$$ f(x) = \left\{\begin{matrix}
1,\ x=1 \\
1 + \frac{1}{x} \sum_{i=1}^{x-1}f(i),\ x>1\end{matrix}\right. $$
粗略估计,可以列出以下方程及初值条件:
$$ \left\{\begin{matrix}
g(1) = 1 \\
g(x) = 1 + \frac{1}{x} \int_{1}^{{\color{Red} x}}f(i)\end{matrix}\right. $$
解得$g(x) = lnx + 1$,且$g(x) > f(x)$对于$x>1$成立,因此深度为$x$的出边期望被访问的$O(logx)$次,则总算法时间复杂度为$O(mlogn)$。
【实现】
图中可能存在环,但其实每次以指定点为起始点进行拓扑排序时只可能进入包含起始点的环,因此只需判断目标点是否为起始点即可。
注意代码中恢复现场(入度in数组)的操作。
【代码】
#include <bits/stdc++.h> using namespace std; const int N=2e5+5; int T,n,k,t,in[N],a[N],ans; bool vis[N]; vector<int> out[N]; void bfs(int s){ int res=1,len; queue<int> q; vector<int> v; //记录每次入度-1的点的编号 q.push(s); while (!q.empty()){ int u=q.front(); q.pop(); vis[u]=1; len=out[u].size(); for (int i=0;i<len;i++){ in[out[u][i]]--; v.push_back(out[u][i]); // if (out[u][i]==s||in[out[u][i]]) continue; res++; q.push(out[u][i]); } } len=v.size(); for (int i=0;i<len;i++) in[v[i]]++; //恢复in数组 ans=max(ans,res); } int main() { scanf("%d",&T); for (int id=1;id<=T;id++){ scanf("%d",&n); for (int i=1;i<=n;i++) out[i].clear(),a[i]=i,vis[i]=0; for (int i=1;i<=n;i++){ scanf("%d",&in[i]); for (int j=1;j<=in[i];j++){ scanf("%d",&t); out[t].push_back(i); } } random_shuffle(a+1,a+n+1); ans=0; for (int i=1;i<=n;i++){ if (vis[a[i]]) continue; bfs(a[i]); } printf("Case #%d: %d\n",id,ans); } return 0; }
—启发式合并—
启发式算法其实就是根据直觉对一些算法的优化。启发式合并的典型做法就是在集合合并时,将小集合往大集合里合并,这样可以保证每次合并集合大小至少翻倍,因此每个点最多被合并$logn$次,算法时间复杂度为$O(nlogn)$。其中树上启发式合并可以参考树上启发式合并 - OI Wiki (oi-wiki.org)
根据之前的分析,本题中的结点根据染黑关系,最终可划分为若干颗互不相交的树。这一过程可以通过合并实现:$I_{S_v}$表示$S_v$的前驱(其实就是$S_v$这棵树的根的前驱,因为其他点的前驱必然已经在$S_v$中),若$I_{S_v} \in S_u$,则$S_v$和$S_u$可以合并,同时要合并其出边。
运用启发式合并,每次将出边少的树向出边多的树里合并。点的合并用并查集,出边的合并可以用 set 解决:用 set 存储入边和出边,u 向 v 合并时,将 u 的出边丢到 v 的出边里去,同时从其指向的点的入边中删去 u 加入 v。每个点和每条边最多被合并$logn$次,时间复杂度为$O((n+m)logn)$,set 操作$O(logn)$,总复杂度为$O((n+m)log^2n)$。
【实现】
可以用队列存储需要合并的点对(bfs),也可以递归(dfs)。但 dfs 貌似快不少,有可能是队列的锅。
每次将 u 向 v 合并后把 v 到 u 的边(如果存在的话)删去,这样可以保证树内部的边不再被合并(因为我们不关心)。
【代码】
用的 dfs,注释掉的部分为 bfs。
[1]和[2]处标注了两个算法理解问题。
#include <bits/stdc++.h> using namespace std; const int N=2e5+5; int T,n,k,t,f[N],sz[N],ans; set<int> in[N],out[N]; //queue<pair<int,int>> q; int find(int x){ return f[x]==x?x:f[x]=find(f[x]); } void merge(int u,int v){ u=find(u),v=find(v); //[1]找到u,v所在树的代表点(注意这并不等同于树根, //因为合并时是按照出边多少而不是谁指向谁) if (u==v) return; if (out[u].size()>out[v].size()) swap(u,v); //u向v合并 f[u]=v; sz[v]+=sz[u]; ans=max(ans,sz[v]); vector<pair<int,int>> q; for (auto to:out[u]){ //[2]不用担心由于to不一定是其所在树的代表点 out[v].insert(to); //而导致其所在树的入边被分散存储 in[to].erase(u); //因为to必然是树根,而只有树根可能有来自树外部的入边 in[to].insert(v); //这也是合并时不合并入边的原因 if (in[to].size()==1) q.push_back({v,to}); } out[v].erase(u); //避免树内部的边被重复计算,可以极大加速 for (auto [x,y]:q) merge(x,y); } int main() { scanf("%d",&T); for (int id=1;id<=T;id++){ scanf("%d",&n); for (int i=1;i<=n;i++) f[i]=i,sz[i]=1,in[i].clear(),out[i].clear(); ans=1; //最小为1 for (int i=1;i<=n;i++){ scanf("%d",&k); for (int j=1;j<=k;j++){ scanf("%d",&t); in[i].insert(t); out[t].insert(i); } //if (k==1) q.push(make_pair(*in[i].begin(),i)); } /*while (!q.empty()){ merge(q.front().first,q.front().second); q.pop(); }*/ for (int i=1;i<=n;i++) if (in[i].size()==1) merge(*in[i].begin(),i); printf("Case #%d: %d\n",id,ans); } return 0; }
【背包+多项式】H
TBC.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号