Least-Square Estimation
刚刚用BioNJ跑完了一波数据,老板和我说这个算法其实挺简单的,你可以自己写一个(主要是BIONJ软件本身和Philip以及MEGA对输入文件要求都比较严,不方便处理),所以我初步学习了一下最原始的NJ树的构建方法
算法源于 The Neighbor-joining Method: A New Method for Reconstructing Phylogenetic Trees
假设我们有一棵无根树具有\(n\)个叶节点,\(n-1\)个内部节点,\(2n-3\)条边(edge,边的数量简记为\(N_E\)),以及由两两叶节点构成的\(\frac{n(n-1)}{2}\)条路径(path,路径的数量简记为\(N_P\))
对于边我们可以构建一个向量\(v_E\)(vector of edge)表示每一条边的长度
对于路径我们可以构建一个向量\(v_P\)(vector of path)表示每一条路径的长度,叶节点距离矩阵\(\{D_{ij}\}\)展开后的形式
于是我们可以构建一个矩阵(A),它的列数等于\(N_E\),它的行数等于\(N_P\),每一个元素等于1或者0,它表示一条边是否存在于某一个路径当中,或者说一条路径是由哪几个边组成的
如
\[
\left[\begin{array}{l}
1&1&0&0&0&0\\
1&0&1&0&0&1\\
1&0&0&1&0&1\\
1&0&0&0&1&1\\
0&1&1&0&0&1\\
0&1&0&1&0&1\\
0&1&0&0&1&1\\
0&0&1&1&0&0\\
0&0&1&0&1&0\\
0&0&0&1&1&0\\
\end{array}\right]
\]
于是我们可以得到一个关于边长与路径长的线性方程组
\[A\cdot v_{E}=v_{P}
\]
\[A^{T}Av_{E}=A^{T}v_{P}
\]
我们记
\[B = A^TA
\]
B是一个对称矩阵,它表示的是两条边同时出现的路径数量
于是我们能够得到
\[
v_{E} = B^{-1}A^{T}v_{P}
\]
这就是我们计算树中各个边长的方法,最理想的方法
但是我们不可能遍历树空间,来找到一个边长之和最小的树结构,所以NJ法中采取的方法是迭代寻找一个局部最优
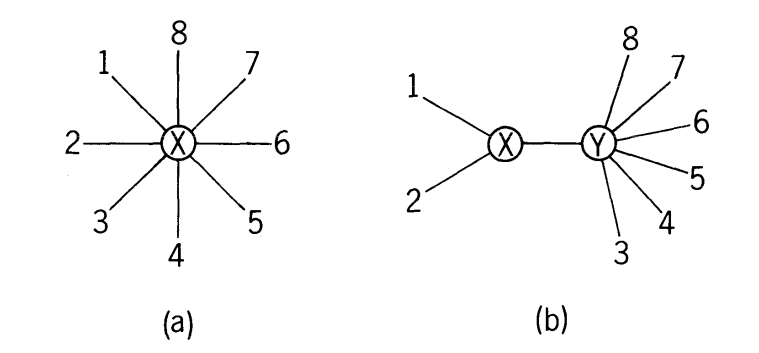
假设我们有一个初始的star-structure的树,我们需要从中将两个OTU(operational taxonomic unit)提取出,并连接到另一个内部节点上,并计算这样的一棵树的边长之和,遍历所有选择方式,共\(C_n^2\)种,选择边长之和最小的那一种树。
![]()
那么之前提到的矩阵B可以写成如下形式(其中N是边[edge]的数量)
\[v_E = [L_{1X},L_{2X},L_{3Y},L_{4Y},...,L_{NY},L_{XY}]\\
\]
\[v_P = [D_{12},D_{13},D_{14},D_{15},...D_{1N},D_{23},D_{24},...D_{2N},...D_{(N-1)N}]
\]
\[
B = \left[
\begin{array}{l}
N-1 & 1 & 1 & ... & 1 & N-2\\
1 & N-1 & 1 & ... & 1 & N-2\\
1 & 1 & N-1 & ... & 1 & 2\\
... & ... &... &...&...&...\\
1 & 1 & 1 & ... & N-1 & 2\\
N-2 & N-2 & 2 & ... & 2 & 2(N-2)\\
\end{array}
\right]
\]
上述公式为理论推导,能力有限,具体解的过程就跳过了,最后可以得到下面化简的公式便于我们进行计算
这里声明,下述公式中"1"和"2"代表选中进行研究的两个叶节点,X为两个叶节点所连的新的内部节点,Y为其它叶节点所连的内部节点,X和Y之间由一条边相连
\[
L_{1X} = \frac{1}{2}D_{12}+\frac{1}{2(N-2)}(P-Q)\newline
\quad\\*
\]
\[L_{1X} = \frac{1}{2}D_{12}+\frac{1}{2(N-2)}(Q-P)\\*
\quad\\*
\]
\[L_{iY} = \frac{1}{N-2}U_i-\frac{1}{(N-2)^2}(P+Q)-\frac{N-4}{(N-2)^2(N-3)}V,\quad(3\le i \le N)\\*
\quad\\*
\]
\[L_{XY} = \frac{1}{2(N-2)}(P+Q)-\frac{1}{2}D_{12}-\frac{1}{(N-2)(N-3)}V\\*
\quad\\*
\]
\[P = \sum^{N}_{j=3}{D_{1j}}\\*
\quad\\*
\]
\[Q = \sum^{N}_{j=3}{D_{2j}}\\*
\quad\\*
\]
\[U_i = \sum^{N}_{j=1,j\ne i}D_{ij}(i \ge 3)\\*
\quad\\*
\]
\[V = \sum_{3\le j < k}D_{jk}\\*
\quad\\*
\]
上述等式可计算自行验证
同时有将两个叶节点支出后的树的边长之和\(S_{12}\)的计算方式:
\[
S_{12} = \frac{1}{2(N-2)}(P+Q) + \frac{1}{2}D_{12}+\frac{1}{N-2}V
\]
\[
S_{12} = \frac{1}{2(N-2)}\sum_{j=3}^{N}{D_{1j}+D_{2j}} + \frac{1}{2}D_{12}+\frac{1}{N-2}\sum_{3\le i < j}^{N}{D_{ij}}
\]
\[
S_{12} = \frac{1}{2(N-2)}\sum_{j=3}^{N}{(L_{1X}+L_{2X}+2L_{XY}+2L_{Yj})} + \frac{1}{2}(L_{1X}+L_{2X})+\frac{N-3}{N-2}\sum_{j=3}^{N}{L_{Yj}}
\]
\[S_{12} = L_{1X}+L_{2X}+L_{XY}+\sum_{j=3}^{N}{L_{Yj}}
\]
之前提到我们是要寻找一个局部最优解,所以我们要遍历每一对叶节点,找到\(S_{12}\)最小的那一对叶节点,我们假设其名为\(A\),\(B\),并将其合并成一个新的叶节点\(\{A,B\}\)
新的叶节点与其它叶节比如叶节点\(C\)的距离\(D_{\{A,B\}C}\),为\(A\)和\(B\)到\(C\)的距离的均值
\[
D_{\{A,B\}C} = \frac{D_{AC}+D{BC}}{2}
\]
基于此构建新的距离矩阵 \(\{D_{ij}^{new}\}\)
我们不断重复上述步骤就可以得到一个完整的NJ树
NJ树本身是基于ME的(minimum evolution principle),相比于其它的构建系统发育树的方法,它速度非常快,后续衍生出来的还有BIONJ,FastME等等基于距离的构建系统发育树的方法,但是建树精度上不如ML或者Bayes基于替换模型的方法




 浙公网安备 33010602011771号
浙公网安备 33010602011771号