2018.09.08模拟总结
毒瘤的九校联考的终于开始了,而且学姐还说这两天的题出的特别“好“,我就感觉离爆零不远了……
T1 restaurant
这道题其实真的是一个完全背包送分题,然而当时的我就是不知咋的没想出来:一看题就觉得此题很难(难个矩阵啊),然后又感觉T2好像可做(实际上并不可做),就先贪心打了个暴力……
实际上这真是完全背包板子,只要把做每一盘菜的所有时间算出来就行了。
不多说,上代码

1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 #include<cstdlib> 7 #include<cctype> 8 #include<vector> 9 #include<stack> 10 #include<queue> 11 using namespace std; 12 #define enter puts("") 13 #define space putchar(' ') 14 #define Mem(a) memset(a, 0, sizeof(a)) 15 typedef long long ll; 16 typedef double db; 17 const int INF = 0x3f3f3f3f; 18 const db eps = 1e-8; 19 const int maxn = 5e3 + 5; 20 inline ll read() 21 { 22 ll ans = 0; 23 char ch = getchar(), last = ' '; 24 while(!isdigit(ch)) {last = ch; ch = getchar();} 25 while(isdigit(ch)) {ans = ans * 10 + ch - '0'; ch = getchar();} 26 if(last == '-') ans = -ans; 27 return ans; 28 } 29 inline void write(ll x) 30 { 31 if(x < 0) x = -x, putchar('-'); 32 if(x >= 10) write(x / 10); 33 putchar(x % 10 + '0'); 34 } 35 36 int n, m, Tmax; 37 ll v[maxn], c[maxn]; 38 ll dp[maxn]; 39 40 void init(int T) 41 { 42 for(int i = 1; i <= T; ++i) dp[i] = 0; 43 } 44 45 int main() 46 { 47 freopen("restaurant.in", "r", stdin); 48 freopen("restaurant.out", "w", stdout); 49 int T = read(); 50 while(T--) 51 { 52 n = read(), m = read(); Tmax = read(); 53 init(Tmax); 54 for(int i = 1; i <= n; ++i) c[i] = read(), v[i] = read(); 55 for(int i = 1; i <= m; ++i) c[i + n] = read(), v[i + n] = read(); 56 for(int i = 1; i <= m; ++i) 57 for(int j = 1; j <= n; ++j) c[i + n] += read() * c[j]; 58 for(int i = 1; i <= n + m; ++i) 59 for(int j = c[i]; j <= Tmax; ++j) 60 dp[j] = max(dp[j], dp[j - c[i]] + v[i]); 61 write(dp[Tmax]); enter; 62 } 63 return 0; 64 }
T2 olefin
考试的时候我觉得和我周五做的题有点像,感觉是什么跟树的直径有关的题,然后简单的推了一会儿,就开始码代码,然而快一个点了却只能过小样例,大样例不知怎么的就是差一点儿。回家才知道是因为我自以为选任意一个直径就行了,实际上是不对的,因为某些点不在选的这条直径上,却在可能其他直径上。反正调了快2个点,最终还是放弃……
!!!时隔五天,我终于来更新正解了!!!
题解说什么换根dp,反正我就感觉是某种树形dp吧,随便怎么叫~~
首先有一个数组dep[u]表示以u为根节点的子树中,离u最远的点的距离,这个一遍dfs维护就可以了。
然后就可以想一想如何维护每一个节点的答案了:对于u的一个子节点v,ans[v] 一定等于dep[v]加上某条链,我们令fro[v]表示这条链的长度。然后就是维护这个数组了:
首先肯定有fro[v] = max(fro[v], fro[u] + 1).
不过fro[v]可能也在u的子树中:于是我们先求出u的子树中的最长链和次长链经过的u的儿子的编号first, second。然后对于v,有这两种情况:
1.最长链经过了v(就是v == first),那么ans[v] = max(ans[v], dep[v] + 2 + dep[second]),加2是因为有v->u,u->second这两条边。同理还要用dep[first] + 2来更新fro[to]
2.最长链没经过v,那么如果次长链存在的话,ans[v] = max(ans[v], dep[v] + 2 + dep[first]).然后再用dep[second] + 2更新fro[to].
然后就会发现其实这两个情况很像~~

1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 #include<cstdlib> 7 #include<cctype> 8 #include<vector> 9 #include<stack> 10 #include<queue> 11 using namespace std; 12 #define enter puts("") 13 #define space putchar(' ') 14 #define Mem(a, x) memset(a, x, sizeof(a)) 15 #define rg register 16 typedef long long ll; 17 typedef double db; 18 const int INF = 0x3f3f3f3f; 19 const db eps = 1e-8; 20 const int maxn = 1e5 + 5; 21 inline ll read() 22 { 23 ll ans = 0; 24 char ch = getchar(), last = ' '; 25 while(!isdigit(ch)) {last = ch; ch = getchar();} 26 while(isdigit(ch)) {ans = ans * 10 + ch - '0'; ch = getchar();} 27 if(last == '-') ans = -ans; 28 return ans; 29 } 30 inline void write(ll x) 31 { 32 if(x < 0) x = -x, putchar('-'); 33 if(x >= 10) write(x / 10); 34 putchar(x % 10 + '0'); 35 } 36 37 int T, n, m; 38 vector<int> v[maxn]; 39 int ans[maxn], fro[maxn], dep[maxn]; 40 41 void init() 42 { 43 for(int i = 0; i < maxn; ++i) v[i].clear(); 44 Mem(ans, 0); Mem(dep, 0); Mem(ans, 0); 45 } 46 47 void dfs1(int now) 48 { 49 for(int i = 0; i < (int)v[now].size(); ++i) 50 { 51 dfs1(v[now][i]); 52 dep[now] = max(dep[now], dep[v[now][i]] + 1); 53 } 54 } 55 56 #define pr pair<int, int> 57 #define scd second 58 #define fst first 59 void dfs2(int now) 60 { 61 pr p(0, 0); //first最长链,second次长链 62 for(int i = 0; i < (int)v[now].size(); ++i) 63 { 64 int to = v[now][i]; 65 ans[to] = max(ans[to], dep[to] + 1 + fro[now]); 66 fro[to] = max(fro[to], fro[now] + 1); 67 if(dep[to] >= dep[p.scd]) p.scd = to; //跟新u的最长和次长链 68 if(dep[p.scd] >= dep[p.fst]) swap(p.scd, p.fst); 69 } 70 for(int i = 0; i < (int)v[now].size(); ++i) 71 { 72 int to = v[now][i]; 73 if(to != p.fst) 74 { 75 ans[to] = max(ans[to], dep[to] + 2 + dep[p.fst]); 76 fro[to] = max(fro[to], dep[p.fst] + 2); 77 } 78 else if(p.scd) 79 { 80 ans[to] = max(ans[to], dep[to] + 2 + dep[p.scd]); 81 fro[to] = max(fro[to], dep[p.scd] + 2); 82 } 83 dfs2(to); 84 } 85 } 86 87 int main() 88 { 89 read(); T = read(); 90 while(T--) 91 { 92 init(); 93 n = read(); m = read(); 94 for(int i = 2; i <= n; ++i) v[read()].push_back(i); 95 dfs1(1); dfs2(1); 96 for(int i = 1; i <= m; ++i) write(ans[read()]), i == m ? enter : space; 97 } 98 return 0; 99 } 100 /* 101 0 102 1 103 10 3 104 1 2 3 1 4 6 7 3 8 105 10 7 9 106 */
写完题解后发现这道题其实不是很难……
T3 tromino
此题直截了当的说:那是相当的毒瘤!推了半天dp式,然后终于发现有两种情况是分不出独立的一块的,于是一顿神算搞到了n<=5的解,结果竟然因为有些该删的东西没删然后就CE了……白白丢了10分……
那正解是啥咧?状压(ye)dp!反正我是想不到。
先不说状压,先想想dp的顺序:数据范围很大,所以一个一个填可定行不通(而且状态不好想),而是应该一列一列去填,然后我们规定这一列必须填满,而且必须紧挨着这一列开始填,也就是说,如果这一列的某一个格子满了,就不能挨着他再往右填。为什么要规定个顺序?就是为了防止统计到重复的情况。
那么状态是酱紫的:当前3 * 2 的方格中格子的填充情况。什么意思呢?还得上图:
比如我们称这样的情况为0号情况(就叫f0吧):

没错就是什么也没填。然后我们想一下他能转化成啥情况:

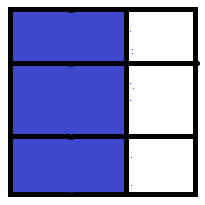
其中一种填法就是三个横着的1 * 3 骨牌全填上。然后因为接下来要往后窜一列,所以f0能转化到的其中一种情况就是右面的那幅图。
以此类推,我们还能从f0衍生出很多别的情况,同理,其他情况也可以互相转化,然后我在纸上画了半天,一共有9种情况。
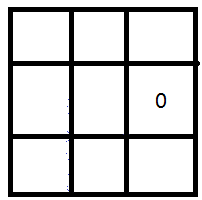

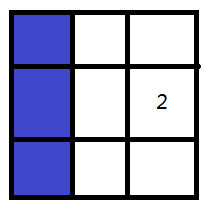
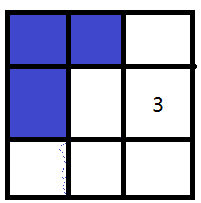
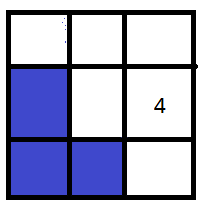
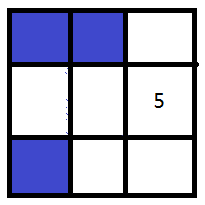


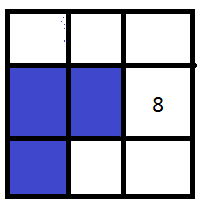 (画的我真不容易)
(画的我真不容易)
然后举个例子,画一画就可以得出5号可以由0号和4号转移过来,即f5 = f0 +f4。同理f0到f8的转移方程我们都可以画出来,这样整个dp方程组就得出来了。(我才不会都写出来,太累)。
然而有这些dp方程还AC不了这题,因为n实在太大了,那么怎么优化咧:
1.矩阵快速幂:由上面的转移方程,可以很容易得到转移矩阵,然后就有矩阵快速幂啦。
2.十进制快速幂:为啥么要这么干咧?考虑普通的快速幂:一般都是二进制的。然而题中的输入很显然是一个高精度数,自然是以十进制存的,那么一位一位的运算,十进制快速幂自然是最合适的了。举个例子:425 = (42)10 * 45。可见刚开始的底数,也就是4,我们可以预处理(既然数字可以,那矩阵自然也是行的通的),而后面的运算就没办法了,只能现算。
代码中我原本想x10用二进制快速幂算的,结果TLE了,然后就改成了x10 = x4 * x4 * x2。
发一下我可爱的代码吧:

1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 #include<cstdlib> 7 #include<cctype> 8 #include<vector> 9 #include<stack> 10 #include<queue> 11 using namespace std; 12 #define enter puts("") 13 #define space putchar(' ') 14 #define Mem(a) memset(a, 0, sizeof(a)) 15 #define rg register 16 typedef long long ll; 17 typedef double db; 18 const int INF = 0x3f3f3f3f; 19 const db eps = 1e-8; 20 const int mod = 998244353; 21 const int maxn = 4e4 + 5; 22 inline ll read() 23 { 24 ll ans = 0; 25 char ch = getchar(), last = ' '; 26 while(!isdigit(ch)) {last = ch; ch = getchar();} 27 while(isdigit(ch)) {ans = ans * 10 + ch - '0'; ch = getchar();} 28 if(last == '-') ans = -ans; 29 return ans; 30 } 31 inline void write(ll x) 32 { 33 if(x < 0) x = -x, putchar('-'); 34 if(x >= 10) write(x / 10); 35 putchar(x % 10 + '0'); 36 } 37 38 int n, b[maxn], len; 39 char c[maxn]; 40 41 struct Mat 42 { 43 ll a[10][10]; 44 Mat() {Mem(a);} 45 Mat operator * (const Mat& other)const 46 { 47 Mat ret; 48 for(rg int i = 0; i < 9; ++i) 49 for(rg int j = 0; j < 9; ++j) 50 for(rg int k = 0; k < 9; ++k) 51 ret.a[i][j] += a[i][k] * other.a[k][j], ret.a[i][j] %= mod; 52 return ret; 53 } 54 }; 55 56 const int f[9][9] = { 57 {1, 0, 1, 0, 0, 0, 0, 0, 0}, 58 {1, 0, 0, 0, 0, 0, 0, 0, 0}, 59 {2, 1, 0, 1, 1, 1, 1, 0, 0}, 60 {1, 0, 0, 0, 0, 0, 0, 0, 1}, 61 {1, 0, 0, 0, 0, 0, 0, 1, 0}, 62 {1, 0, 0, 0, 1, 0, 0, 0, 0}, 63 {1, 0, 0, 1, 0, 0, 0, 0, 0}, 64 {0, 0, 0, 0, 0, 1, 0, 0, 0}, 65 {0, 0, 0, 0, 0, 0, 1, 0, 0} 66 }; 67 68 Mat P[10]; 69 void init() 70 { 71 Mat F; 72 for(rg int i = 0; i < 9; ++i) 73 for(rg int j = 0; j < 9; ++j) F.a[i][j] = f[i][j]; 74 for(rg int i = 0; i < 9; ++i) P[0].a[i][i] = 1; 75 for(rg int i = 1; i < 10; ++i) P[i] = P[i - 1] * F; 76 } 77 78 Mat tp; 79 Mat qp_10() 80 { 81 Mat ret = P[0]; 82 for(rg int i = 1; i <= len; ++i) 83 { 84 tp = ret = ret * ret; 85 ret = ret * ret; 86 ret = ret * ret * tp * P[b[i]]; 87 } 88 return ret; 89 } 90 91 int main() 92 { 93 freopen("tromino.in", "r", stdin); 94 freopen("tromino.out", "w", stdout); 95 scanf("%s", c + 1); 96 len = strlen(c + 1); 97 for(int i = 1; i <= len; ++i) b[i] = c[i] - '0'; 98 init(); 99 Mat Ans = qp_10(); 100 write(Ans.a[0][0]); enter; 101 return 0; 102 }
挺短的。
然后我调了1个点,我不会告诉你是因为我的矩阵刚开始写成这样的:

1 const int f[9][9] = { 2 1, 0, 1, 0, 0, 0, 0, 0, 0, 3 1, 0, 0, 0, 0, 0, 0, 0, 0, 4 2, 1, 0, 1, 1, 1, 1, 0, 0, 5 1, 0, 0, 0, 0, 0, 0, 0, 1, 6 1, 0, 0, 0, 0, 0, 0, 1, 0, 7 1, 0, 0, 0, 1, 0, 0, 0, 0, 8 1, 0, 0, 1, 0, 0, 0, 0, 0, 9 0, 0, 0, 0, 0, 1, 0, 0, 0, 10 0, 0, 0, 0, 0, 0, 1, 0, 0 11 };
【宛若智障】
还有一个很重要的优化,然而我太菜了不会:就是把上述矩阵高斯消元然后怎么一搞,就变成了6 * 6的了,一定快了不少。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号