中文分词原理和代码实践
1 简介和分类
中文分词(Chinese Word Segmentation) 指的是将一个汉字序列切分成一个一个单独的词。分词就是将连续的字序列按照一定的规范重新组合成词序列的过程。
现有的分词算法可分为三大类：基于字符串匹配的分词方法、基于理解的分词方法和基于统计的分词方法（本文主要讲述该方法）
1.1基于字符串匹配的分词方法：
这种方法又叫做机械分词方法，它是按照一定的策略将待分析的汉字串与一个"充分大的"机器词典中的词条进行配，若在词典中找到某个字符串，则匹配成功（识别出一个词）
1）正向最大匹配法（由左到右的方向）
2）逆向最大匹配法（由右到左的方向）:
3）最少切分（使每一句中切出的词数最小）
4）双向最大匹配法（进行由左到右、由右到左两次扫描）
1.2基于理解的分词方法：
这种分词方法是通过让计算机模拟人对句子的理解，达到识别词的效果。其基本思想就是在分词的同时进行句法、语义分析，利用句法信息和语义信息来处理歧义现象。它通常包括三个部分：分词子系统、句法语义子系统、总控部分。在总控部分的协调下，分词子系统可以获得有关词、句子等的句法和语义信息来对分词歧义进行判断，即它模拟了人对句子的理解过程。这种分词方法需要使用大量的语言知识和信息。由于汉语语言知识的笼统、复杂性，难以将各种语言信息组织成机器可直接读取的形式，因此目前基于理解的分词系统还处在试验阶段。
1.3基于统计的分词方法：
给出大量已经分词的文本，利用统计机器学习模型学习词语切分的规律（称为训练），从而实现对未知文本的切分。例如最大概率分词方法和最大熵分词方法等。 随着大规模语料库的建立，统计机器学习方法的研究和发展，基于统计的中文分词方法渐渐成为了主流方法。
主要统计模型：N元文法模型（N-gram），隐马尔可夫模型（Hidden Markov Model ，HMM），最大熵模型（ME），条件随机场模型（Conditional Random Fields，CRF）等
2 正向最大匹配法和逆向最大匹配法
使用trie树建立词典，进行正向和反向查找
例如：大学生活动中心
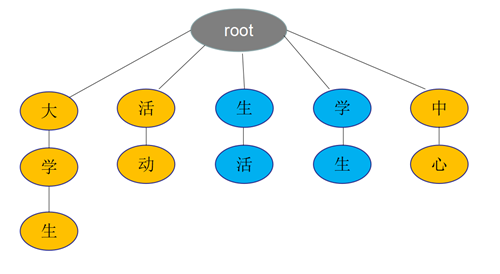
正向最大匹配法：根据中文句子，从左到右去trie树匹配查找长度最大的词语。
如上图，大学生/活动/中心，先匹配出"大学生"，然后"活动"，最后"中心"
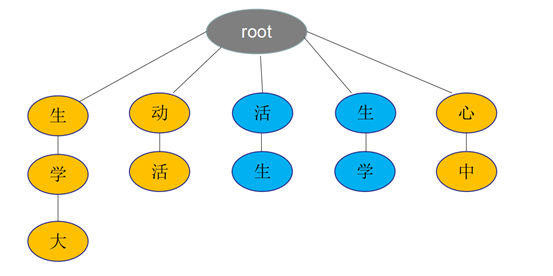
逆向最大匹配法：根据中文句子，从右（句子末尾）到左去trie树匹配查找长度最大的词语。
如上图，大学生/活动/中心，先匹配出"心中"，然后"动活"，最后"生学大"
3 基于统计分词介绍
3.1 概率语言模型
假设要分出来的词在语料库和词表中都存在，则最简单的切方法是按词计算概率，而不是按字计算概率（没有意义）。
分词问题，可以看作：输入一个字串C=c1,c2,c3...cn，输出一个词串S=w1,w2,w3...wm，m<=n,即分出的单词数m<=原来字串的长度。对于一个特定的字串C都有多种切分方案S，分词的目标就是找出最有可能出现的S方案，即使得P(S|C)概率最大，P(S|C)就是由字符串C切分出S方案的概率，也就是对输入字符串切分出最有可能的词序列。
例如，对于输入字符串"南京市长江大桥"，有下面2中切分方案S:
S1: 南京市/长江/大桥
S2: 南京/市长/江大桥
计算条件概率P(S1|C)，P(S2|C)，选择出概率较大的作为切分方案。
P(C)表示字串C在语料库中出现的概率。比如语料库中有1万的句子，"南京市长江大桥"在该语料库中出现了1次，则P(C)=P(南京市长江大桥)=万分之一。
由条件概率公式得知：p(C,S)=P(S|C)*P(C)=P(C|S)*P(S)，
故贝叶斯公式：p(S|C)=p(C|S)*p(S)/p(C)。
其中：P(C)是一个固定值，另外从词串恢复到字串的概率只有唯一一种方式，故P(C|S)=1
所以比较P(S1|C),P(S2|C)的大小，可以化简为：
P(S1|C)/P(S2|C)=P(S1)/P(S2)
因为P(S1)=p(南京市,长江,大桥)=P(南京市)P(长江)P(大桥)>P(S2)=p(南京,市长,江大桥)=P(南京)P(市长)P(江(大桥)，故选择S1
3.1.1一元模型
对于不同的S，m的值是不一样的，一般地，m越大，P(S)与越小，即分出的词越多，概率越小
P(S)计算公式：P(S)=P(w1)*P(w2)*P(w3)...P(wn)，
P(wi)=(wi在语料库中出现的次数n) / (语料库中的总词数N)
该公式是基于独立假设的，即词与词之间是相互独立的，因此该公式也叫一元模型
3.1.2 N元模型
假设在日本，和服是一个常见词，按照一元模型，可能会把"产品和服务"切分为：产品/和服/务，为了切分更准确需要考虑词所处的上下文
N元模型使用n个单词组成的序列来衡量切分方案的合理性：
估计单词w1出现后，w2出现的概率P(w1,w2)= P(w1)P(w2|w1)
同理，P(w1,w2,w3)= P(w1,w2)*P(w3|w1,w2)=P(w1)P(w2|w1)*P(w3|w1,w2)
更加一般的形式：
P(w1,w2,w3...wn)= P(w1)P(w2|w1)*P(w3|w1,w2)...*P(wn|w1,w2,w3...wn-1)
如果简化成一个词的出现仅仅依赖前面一个词，则为二元模型（Bigram）
P(S)=P(w1,w2,w3...,wn)≈P(w1)P(w2|w1)*P(w3|w2)...P(wn|wn-1)
3.1.3 马尔可夫模型（MM：Markov Model）
N元模型又可以看作马尔可夫模型：每个状态只依赖之前有限个状态
参数：
状态，由数字表示，假设共有M个
初始概率，由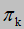
表示
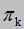
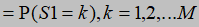
状态转移概率，由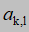
表示
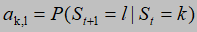k,l=1,2,...M
3.1.4 隐马尔可夫模型HMM（Hidden Markov Model）
马尔可夫模型是对一个序列建模，但有时我们需要对2个序列建模，
如机器翻译，源语言序列 -> 目标语言序列
语言识别，语言信号序列 -> 文字序列
通常一个序列称为观测序列，一个为隐藏序列，如语言识别中，声波信号为观测序列，记为O，实际上要表达的文字观测不到，记为S，我们要找的就是S，即"说了什么"。
观测序列O中的数据通常是由隐藏序列数据决定的，彼此间相互独立
隐藏序列数据间相互依赖，通常构成了马尔可夫序列
例如语言识别中，每段声波信号是相互独立的，有对应的文字决定
对应的文字序列中，文字间相互依赖，构成马尔可夫序列
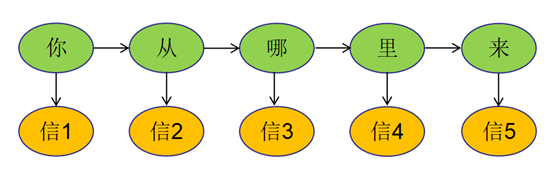
观测和隐藏序列共同构成隐马模型：
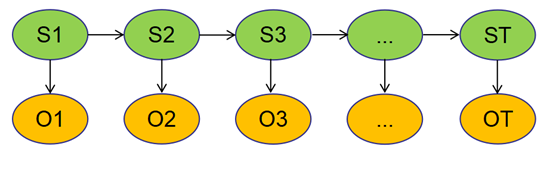
O(O1,O2,...OT)，观测序列，Ot只依赖St
S(S1,S2,...ST)，状态序列（隐藏序列），S是马尔可夫序列，假设一阶马尔可夫，则St+1只依赖于St
HMM参数
状态由数字表示，假设共有M个
观测由数字表示，假设共有N个
初始概率（所有初始状态中k状态的样本数/所有初始状态的样本数），由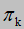
表示
状态转移概率（k状态到l状态的概率a(k,l)=所有k状态下到l的频次/所有k状态的频次），由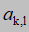
表示
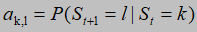k,l=1,2,...M
发射概率（由k状态发射到u观测值的概率=k状态下观测值u的频次/k状态的频次），由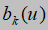
表示
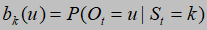u=1,2,...N k=1,2,...M
HMM生成过程：
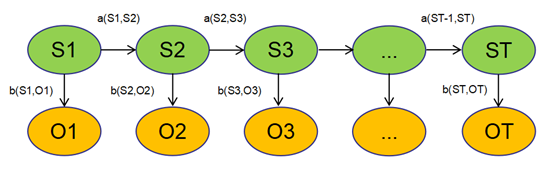
先生成第一个状态，然后依次由当前状态生成下一个状态，最后每个状态发射出一个观测值
公式：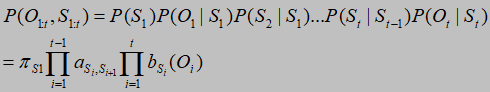
注意：p(S1)就是初始状态概率，当前观测值Ot依赖于当前状态St，当前状态St依赖于前一个状态St-1，该公式表示的是生成序列Ot和St的概率
问题：
根据给定的HMM参数（πk,a(k,l),bk(u)）和观测序列O，如何求隐藏序列S
分析：根据公式，每个可能的S序列都能计算出一个概率，而概率最大的那个S序列即为解
4 中文分词代码实践
allfiles.txt 链接：https://pan.baidu.com/s/17Dx5dBQRf8UyLzbvZ1BrGQ
提取码：uggl
''' 隐马尔可夫模型 三个参数θ的计算： 假设隐藏状态共M个 初始状态概率（M）= sum(每篇文章第一个字为k状态的频次) / sum(每篇文章第一个字的状态的频次) 状态转移概率（M*M）= sum(每篇文章k状态到l状态的频次) / sum(每篇文章k状态的频次) 发射概率（M*N，N表示句子的长度）= sum(每篇文章k状态下某观测值Ot的频次) / sum(每篇文章k状态的频次) 训练：样本为allfiles.txt，该文件一行是一篇文章，且每篇文章已经分词 即在已知每篇文章的分词序列后，计算θ，然后根据θ和观测序列O（如一个未分词的句子），计算最佳的隐藏序列S， 知道S后即可分词 θ的计算： 1 遍历每篇文章，计算每篇文章各个字的隐藏状态S（S in {BMES}） 2 统计各个初始状态的频次，某状态的频次，某状态到某状态的频次，某状态到某个文字的频次 3 根据公式计算3种概率 4 结果存储到磁盘 ''' import math import jieba '''读取数据''' wiki_flag=False pre = 'F:\\00-data\\' if wiki_flag: train_file='F:\\00-data\word2vec\\wiki.txt' else: train_file = pre + 'allfiles.txt' save_file = pre + 'out\\hmm\\hyj_hmm.model' # 隐藏状态数量 STATUS_NUM = 4 # 频次为0的默认无穷小概率 min_prob = -100000.0 def get_word_ch_list(word: str): ''' 将词语转换为文字列表 :param word: :return: ''' if word is None or word.strip() == '': return [] res = [] for ch in word: res.append(ch) return res def get_status_list_by_chlist(ch_list: []): ''' 根据词语的文字列表获取隐藏状态列表:BMES ->[0,1,2,3] :param ch_list: :return: BMES ->[0,1,2,3] ''' len_ch = len(ch_list) if len_ch == 0: return [] if len_ch == 1: # S return [3] res = [-1 for i in range(len_ch)] # B res[0] = 0 # E res[-1] = 2 for j in range(1, len_ch - 1): # M res[j] = 1 return res def count_b(b_matrix, ch_list, i, status_list): ''' 发射频次统计 :param b_matrix: :param ch_list: :param i: :param status_list: :return: ''' # 下标为i的文字 ch_i = ch_list[i] # 下标为i的状态 status_i = status_list[i] # 如果某状态下某文字为空，则初始化计数为0 if b_matrix[status_i].get(ch_i, -1) == -1: b_matrix[status_i][ch_i] = 0. b_matrix[status_i][ch_i] += 1 def train_theta(): ''' 训练入口 :return: ''' # 初始状态概率 M个 start_prob = [0. for i in range(STATUS_NUM)] # 状态转移概率矩阵 M*M a_matrix = [[0. for i in range(STATUS_NUM)] for i in range(STATUS_NUM)] # 发射概率矩阵 M*N，N表示某状态下的所有文字种数，由于N不确定，所以用dict存储(key=文字,value=概率) b_matrix = [dict() for i in range(STATUS_NUM)] # 初始状态总数 total_start_status = 0. # 每个状态的总频次数 total_status_dict = dict() with open(train_file, mode='r', encoding='utf-8') as f: ''' readline(): 1、每次读取下一行文件。 2、可将每一行数据分离。 3、主要使用场景是当内存不足时，使用readline()可以每次读取一行数据，只需要很少的内存。 readlines(): 1、一次性读取所有行文件。 2、可将每一行数据分离，从代码中可以看出，若需要对每一行数据进行处理，可以对readlines()求得的结果进行遍历。 3、若内存不足无法使用此方法。 ''' # 一行是一篇文章 line = f.readline() # 文件读完为止 while line and line.strip() != '': print('while line==True') # 每篇文章的所有单词 split()默认分隔符为空格 words = line.strip().split() if len(words) == 0: return # 统计初始状态频次 start_word = words[0] start_ch_list = get_word_ch_list(start_word) start_status_list = get_status_list_by_chlist(start_ch_list) start_prob[start_status_list[0]] += 1. total_start_status += 1 # 一篇文章相当于一个观测序列和一个隐藏序列，文章和文章之间没有关系，所以θ不会跨文章统计 # 每篇文章的隐藏状态序列S article_ch_status_list = [] # 每篇文章的文字序列O article_ch_list = [] # words[:-1]最后一个不是词语，需要过滤 if wiki_flag: word_list=words else: word_list=words[:-1] for word in word_list: # 词语的文字序列 ch_list = get_word_ch_list(word) # 词语的状态序列 status_list = get_status_list_by_chlist(ch_list) if len(ch_list) == 0 or len(status_list) == 0: continue # 将词语序列转换为文章序列 article_ch_list.extend(ch_list) article_ch_status_list.extend(status_list) # 每篇文章的频次统计 article_ch_len = len(article_ch_status_list) for i in range(0, article_ch_len - 1): # 状态转移频次统计 k_status = article_ch_status_list[i] j_status = article_ch_status_list[i + 1] a_matrix[k_status][j_status] += 1. count_status(k_status, total_status_dict) # 发射频次统计 count_b(b_matrix, article_ch_list, i, article_ch_status_list) # 由于i的最大长度减了1，故还要统计每篇文章最后一个字的状态频次和发射频次 count_status(article_ch_status_list[-1], total_status_dict) count_b(b_matrix, article_ch_list, i + 1, article_ch_status_list) line = f.readline() print('count pi:', start_prob) print('count A:', a_matrix) print('count B:', b_matrix) '''计算概率''' print('compute prob...') for i in range(STATUS_NUM): # 初始状态概率 # 概率取对数 prob = start_prob[i] / total_start_status if prob > 0: start_prob[i] = math.log(prob) else: # 如果频次为0 则给一个默认的无穷小概率 start_prob[i] = min_prob # 状态转移概率 for j in range(STATUS_NUM): prob = a_matrix[i][j] / total_status_dict[i] if prob > 0.: a_matrix[i][j] = math.log(prob) else: a_matrix[i][j] = min_prob # 发射概率 for single, count in b_matrix[i].items(): prob = count / total_status_dict[i] if prob > 0.: b_matrix[i][single] = math.log(prob) else: b_matrix[i][single] = min_prob print(' start-prob:', start_prob) print('a-prob:', a_matrix) print('b-prob:', b_matrix) print('save model...') with open(save_file, mode='w', encoding='utf-8') as f: f.write(str(start_prob) + '\n') f.write(str(a_matrix) + '\n') f.write(str(b_matrix) + '\n') print('save done:', save_file) def count_status(k_status, total_status_dict): if total_status_dict.get(k_status, -1) == -1: total_status_dict[k_status] = 0. total_status_dict[k_status] += 1. def viterbi(sentence, sep=' '): ''' 给定一个未分词的句子，使用维特比算法，寻找最优的切分序列S :param sentence: :param sep: 分隔符 :return: 返回不同的分词方案 ''' res = [] # 加载模型 # 初始状态概率 M PI = None # 状态转移概率 M*M A = None # 发射概率 M*N N表示某状态下的文字种数 B = None with open(save_file, mode='r', encoding='utf-8')as f: PI = eval(f.readline()) A = eval(f.readline()) B = eval(f.readline()) # 获取句子的文字列表 ch_list = get_word_ch_list(sentence) sentence_len = len(ch_list) # M*句子长度的矩阵，每个元素是一个数组[hmm概率值，上一列中最好的节点状态S] s_matrix = [[[0., 0] for j in range(sentence_len)] for i in range(STATUS_NUM)] # 找到h层的节点i，使得i到h+1层的j节点的hmm值最大 get_max_hmm_matrix(PI, A, B, ch_list, s_matrix, sentence_len) print('s_matrix:', s_matrix) '''找到hmm概率最大的S序列''' # 最后一列中，hmm最大的节点 best_end = None # 最后一列中，hmm的最大概率 best_p = None best_end_status = None # 最后一列的节点列表 last_node = [] for i in range(STATUS_NUM): end_i = s_matrix[i][-1] last_node.append((end_i[0], end_i[1], i)) if best_p is None or best_p < end_i[0]: best_p = end_i[0] best_end_status = i # best_end=end_i # 最后一列的节点列表以hmm概率倒序排列 last_node = sorted(last_node, key=lambda x: x[0], reverse=True) print(last_node) # 从后往前遍历hmm概率矩阵，找出S序列 s_list = [0 for i in range(sentence_len)] s_list[-1] = best_end_status for col_i in range(1, sentence_len + 1): s_list[sentence_len - col_i] = best_end_status i_node = s_matrix[best_end_status][sentence_len - col_i] best_end_status = i_node[1] # best_end=i_node print(s_list) # 切分句子 BMES 0123 word = '' for ch_i in range(sentence_len): if s_list[ch_i] == 3: word = ch_list[ch_i] res.append(word) word = '' continue if s_list[ch_i] == 2: word += ch_list[ch_i] res.append(word) word = '' continue word += ch_list[ch_i] return res def get_max_hmm_matrix2(PI, A, B, ch_list, s_matrix, sentence_len): ''' 最优路径动态规划 找到最优路径 使得hmm概率最大 分析： 定义在m*n的S矩阵中，i=m-1, j=n-1 , p,p0 in (0,i), q in (0,j) dp[p][q][0],dp[p][q][1]分别表示从（p0,0）位置(第一列某个节点)到达pq位置（q列某个节点p）的最大hmm概率值和q-1列中hmm最大的节点 则dp[p][q][0]= q-1列中的（hmm+ s到节点p的转移概率）最大值的节点s + p节点到文字Oq的发射概率 dp[p][q][0] = max(dp[s][q-1]+ A[s][p]) + B[p][Oq] dp[p][q][1]=s 第一列初始值 dp[p][0]= PI[p]+ B[p][O(0)] :param A: :param B: :param ch_list: :param s_matrix: :param sentence_len: :return: ''' # for p in range(STATUS_NUM): # dp(PI, A, B, ch_list, s_matrix, sentence_len, p, sentence_len - 1) # 递归废弃 直接返回s_matrix return s_matrix # def dp(PI, A, B, ch_list, s_matrix, sentence_len, p, q): # if q == 0: # return init_s_matrix(B, PI, ch_list, s_matrix) # # max_arr = max_dps(PI, A, B, ch_list, s_matrix, sentence_len, p, q) # # if B[p].get(ch_list[q], -1) != -1: # s_matrix[p][q][0] = max_arr[0] + B[p][ch_list[q]] # else: # s_matrix[p][q][0] = max_arr[0] + min_prob # s_matrix[p][q][1] = max_arr[1] # # return [s_matrix[p][q][0], s_matrix[p][q][1]] # # # def max_dps(PI, A, B, ch_list, s_matrix, sentence_len, p, q): # max_prob = None # max_status = None # for s in range(STATUS_NUM): # cur_prob = dp(PI, A, B, ch_list, s_matrix, sentence_len, s, q - 1)[0] + A[s][p] # if max_prob is None or max_prob < cur_prob: # max_prob = cur_prob # max_status = s # # return [max_prob, max_status] # # # def init_s_matrix(B, PI, ch_list, s_matrix): # # 初始化第一列 # max_prob = None # max_status = None # for i in range(STATUS_NUM): # if B[i].get(ch_list[0], -1) != -1: # s_matrix[i][0][0] = PI[i] + B[i][ch_list[0]] # else: # s_matrix[i][0][0] = PI[i] + min_prob # # 第一列不需要存储上一列的最优节点 所以赋值为-1 # s_matrix[i][0][1] = -1 # cur_prob = s_matrix[i][0][0] + B[i][ch_list[0]] # if max_prob is None or max_prob < cur_prob: # max_prob = cur_prob # max_status = i # return [max_prob, max_status] def get_max_hmm_matrix(PI, A, B, ch_list, s_matrix, sentence_len): ''' 找到最优路径 使得hmm概率最大 :param A: :param B: :param ch_list: :param s_matrix: :param sentence_len: :return: ''' # 计算第一列的hmm概率=PI(S1)*B(O1|S1) for i in range(STATUS_NUM): if B[i].get(ch_list[0], -1) == -1: s_matrix[i][0][0] = PI[i] + min_prob else: # 由于概率取了对数，相加即相乘 s_matrix[i][0][0] = PI[i] + B[i][ch_list[0]] s_matrix[i][0][1] = i for ch_j in range(1, sentence_len): # 某一行某个文字可能有M种状态 # 当前列的j for j in range(STATUS_NUM): max_p = None max_status = None # 上一列的i for i in range(STATUS_NUM): # i到j的转移概率 a_ij = A[i][j] # 当前i到j的hmm概率 cur_p = s_matrix[i][ch_j - 1][0] + a_ij if max_p is None or max_p < cur_p: max_p = cur_p max_status = i # j节点的hmm概率和i节点的状态S b_prob = min_prob if B[j].get(ch_list[ch_j], -1) != -1: b_prob = B[j][ch_list[ch_j]] s_matrix[j][ch_j][0] = max_p + b_prob s_matrix[j][ch_j][1] = max_status def read_file(path): with open(path, mode='r', encoding='utf-8') as f: line=f.readline() while line: print(line) line=f.readline() if __name__ == '__main__': # read_file('F:\\00-data\word2vec\\wiki.txt') # train_theta() st = '无边落木萧萧下，不尽长江滚滚来' st2='北京大学生活动中心' st3='南京市长江大桥' seq_list=[st,st2,st3] for s in seq_list: res = viterbi(s) print('hmm:'+str(res)) print('jieba:'+str([x for x in jieba.cut(s,cut_all=False)])) # ch_list = get_word_ch_list(st3) # slist = get_status_list_by_chlist(ch_list) # print(ch_list) # print(slist)
浙公网安备 33010602011771号