数据结构之刷题记录

删除链表中的某个x数据

void Del_x(LinkList& L, ElementType x) {
	LNode* pre = L, * p = L->next, * q;
	while (p != null) {
		if (p->data == x) {
			q = p;
			p = p->next;
			pre->next = p;
			free(q);
		}
		else {
			pre = p;
			p=p->next
		}
	}
}

将两个有序表合成一个有序表，返回有序表

 

bool Merge(Sqlist a, Sqlist b, Sqlist& c) {
	int i = 0, j = 0, k = 0;
	if (a.length + b.length < c.maxSize)//c辅助表无法容纳两个表元素
		return false;
	while (i < a.length && j < b.length) {//从两个表中各取一个，谁小存入c表
		if (a.data[i] = b.data[j]) {
			c.data[k++] = a.data[i++];
		}
		else {
			c.data[k++] = b.data[j++];
		}
	}
	while (i < a.length) {//a表有剩余，全放入c
		c.data[k++] = a.data[i++];
	}
	while (j < b.length) {//b表有剩余，全放入c
		c.data[k++] = b.data[j++];
	}
	c.length = k;
	return true;
}

将顺序表倒置，空间复杂度为O（1）

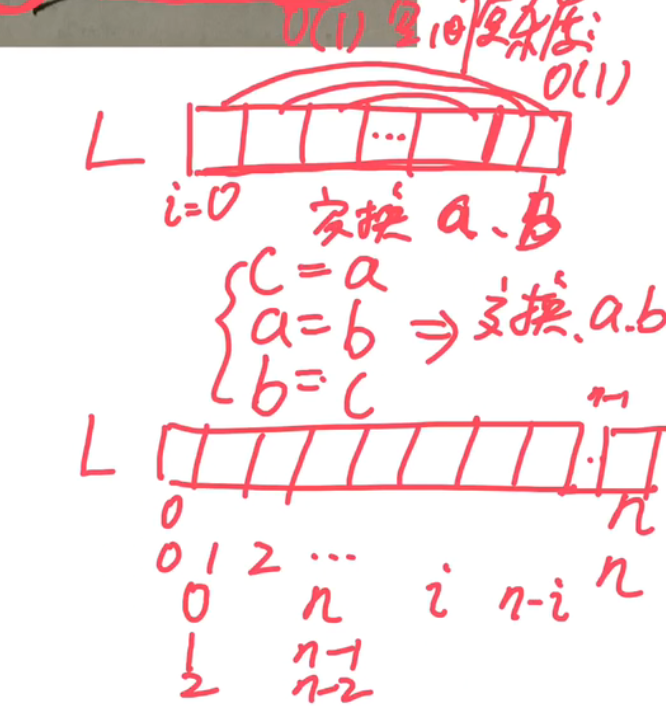
两者交换关系：i   n-i    不过n=L.length-1;

void Reverse(SqList& L) {
	ElemType temp;
	for (int i = 0; i < L.length / 2; i++) {
		temp = L.data[i];
		L.data[i] = L.data[L.length - 1 - i];
		L.data[L.length - 1 - i] = temp;
	}
}

使用递归方法

void Reverse(int* a, int low, int high) {
	if (low < high) {
		swap(a[low], a[high]);
		Reverse(a, low + 1, high - 1);
	}
}

 

 

算法思想：扫描顺序表，记录值为x的个数k,将其中不为x的元素向前移动k个单位

void Del_x(Sqlist& L,ElemType x) {
	int i = 0;
	while (i < L.length) {
		int k = 0;
		if (L.data[i] == x)
			k++;
		else {
			L.data[i - k] = L.data[i];
			
		}
		i++;
       
	}
    L.length=L.length-k;
}

法二：

算法思想：扫描顺序表，保留下不是x的元素(删除所有值为x的元素)，k++记录值不为x元素个数

void Del_x(Sqlist& L,ElemType x) {
	int k = 0;
	for (int i = 0; i < L.length; i++) {
		if (L.data[i] != x)
		{
			L.data[k] = L.data[i];
			k++;
		}
	}
	L.length = k;
}

 

算法思想：

顺序扫描顺序表，k记录值在这两个区间的元素的个数，将值不在这两个区间的元素向前移动k个位置

bool Del_StoT(Sqlist& L, elemType s, elemType t)
{
	if (s >= t || L.length == 0)
		return false;
	int k = 0;
	int i = 0;
	while (i < L.length) {
		if (L.data[i] >= s && L.data[i] <= t)
			k++;
		else
			L.data[i - k] = L.data[i];
	}
	L.length = L.length - k;
	return true;
}

法二：

算法思想：

扫描顺序表，将值不在st之间的元素保留下来（删除值在这两个区间的元素），k记录新的数组的下标

bool Del_StoT(Sqlist& L, elemType s, elemType t)
{
	if (s >= t ||L.length==0)
		return false;
	int k = 0;
	for (int i = 0; i < L.length; i++) {
		if (!(L.data[i] >= s && L.data[i] <= t)) {
			L.data[k] = L.data[i];
			k++;
		}

	}
	L.length = k;
    return true;
}

 

算法思想：第一个元素（不重复），i指向第一个元素，j指向第二个元素，两者依次向后扫描，i,j所指的元素不重复就保留，j向后移动，重复就不保留，j后移，删除所有重复元素

bool Del_same(Sqlist& L) {
	if (L.length == 0)
		return false;
	for (int i = 0, j = 1; j < L.length; j++) {
		if (L.data[i] != L.data[j]) {
			L.data[++i] = L.data[j];
		}
	}
	L.length = i + 1;
	return true;
}

算法思想：

将前m个a1......am逆置，后n个b1.....bn逆置，将m+n个数据逆置一次，三次逆置

void Reverse(Sqlist& L, int low, int high) {
	elemType temp;
	for (int i = 0; i <(high-low+1)/2; i++) {
		temp = L.data[low+i];
		L.data[low+i] = L.data[high - i];
		L.data[high - i] = temp;
	}
}
void exchange(Sqlist& L, int n, int m) {
	Reverse(L, 0, m- 1);
	Reverse(L, m,(m+n)- 1);
	Reverse(L, 0, m + n - 1);
}

 

算法思想：将前面（x0....xp-1)的元素逆置，将后面的(xp,....xn-1)个元素逆置，将逆置完成的所有元素再逆置一次，得出的序列即为所求（三次逆置）

void Reverse(int a[], int from, int to) {
	int temp;
	for (int i = 0; i < (to-from+1)/2; i++) {
		temp = a[from + i];
		a[from + i] = a[to - i];
		a[to - i] = temp;
	}
}
void exchange(int a[], int n, int p) {
	Reverse(a,0,p-1 );
	Reverse(a,p,n-1);
	Reverse(a,0,n-1);
	
}

算法思想：

指针p遍历链表，pre指向p的前驱，minp标记最小值结点，minpre指向minp的前驱，扫描过程中，若p->data<,inp->data,将p,pre分别赋值给minp,minpre,扫描完毕，此时minp指向最小值结点，minpre最小值结点的前驱结点，将minp结点删除即可。

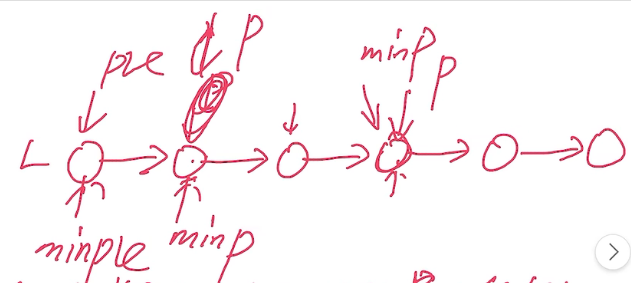
void Del_min(List& L) {
	LNode* p, * pre, * minp, * minpre;
	pre = L;
	p = L->next;
	minp = p;//最小值结点minp
	minpre = pre;//最小值结点的前驱
	while (p != null) {//找最小值结点
		if (minp->data > p->data) {//p所指的结点小于最小值结点的值
			minp = p;
			minpre = pre;
		}
		pre = p;//p,pre向前移动
		p = p->next;
	}
	//删除最小值结点
	minpre->next = minp->next;
	free(minp);
	
}

Linklist CreateList(Linklist&L) {
	LNode* s, int x;
	L = (Linklinst)malloc(sizeof(LNode));
	L->next = null;
	cin >> x;
	while (x != -1) {
		s = (LNode*)malloc(sizeof(LNode));
		s->data = x;
		s->next = L->next;
		L->next = s;
		cin >> x;
	}
	return L;
	
}

Linklist List_TailInsert(Linklist&L) {
	LNode* s, *r;//尾指针r,新指针s
	L = (Linklinst)malloc(sizeof(LNode));//创建头节点
	r = L;//r指向头节点
	cin >> x;//输入x的值
	while (x != -1) {
		s = (LNode*)malloc(sizeof(LNode));//创建s结点
		s->data = x;
		r->next = s;//尾插法插入s结点
		r = s;
		cin >> x;
	}
	r->next = null;
	return L;
	
}

分析：1.头插法

Linklist List_TailInsert(Linklist&L) {
	LNode* p, * r;
	p = L->next;
	L->next = null;
	while (p != null) {
		r = p->next;//保留后继指针，防止断链
		p->next = L->next;//头插法
		L->next = p;
		p = r;
	}
	return L;
	
}

法二：

Linklist List_TailInsert(Linklist&L) {
	LNode* pre,*p, * r;
	pre = L->next;
	p = pre->next;
	r = p->next;
	while (r) {
		p->next = pre;
		pre = p;
		p = r;
		r = r->next;
	}
	p->next = pre;
	L - next = p;
	return L;
	
}

算法思想：

遍历链表，删除在最小值s和最大值t之间的元素。

void del_StoT(Linklist&L,int s,int t) {
	LNode* pre,*p, *q;
	pre = L;
	p = L->next;
	while (p != null) {
		if (p->data < t && p->data >s) {
			pre->next = p->next;
			q = p;
			p = p->next;
			free(q);
		}
		else {
			pre = p;
			p = p->next;
		}
	}
}

LNode search_common(linklist& la, linklist& lb) {
	LNode* p = la->next, * q = lb->next;
	while (p != null) {
		while (q != null) {
			if (p== q) {
				return p;//找到共同结点时返回
			}
			q = q->next;
		}
		p = p->next;
		q = lb->next;
	}
}

共同结点

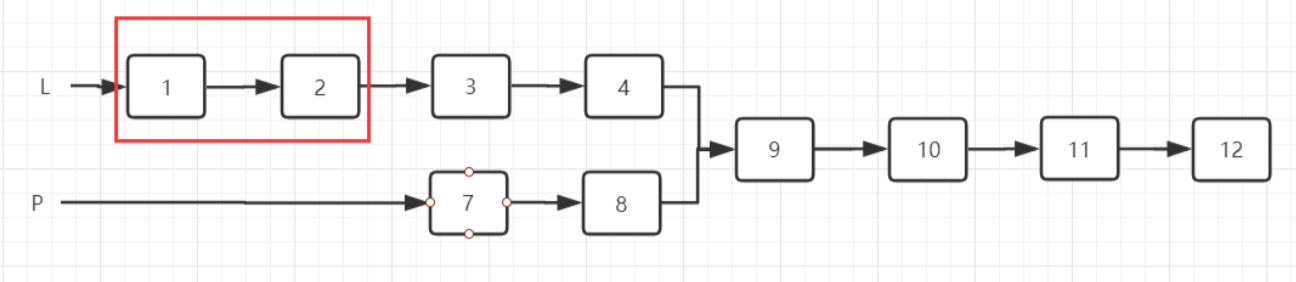
时间复杂度：O（la*lb）

法二：

我们从头节点开始遍历,寻找第一个公共节点,由于两个链表的长度可能不同,我们让两个链表相减得出最长链表多余的部分,然后让长度相同的两个链表,同时开始遍历,找的地址相同的第一个节点,则后面的节点都为公共节点, 

LNode search_common(linklist* la, linklist* lb) {
	int lenA = length(la);
	int lenB = length(lb);
	if (lenA - lenB > 0) {
		k = lenA - lenB;
		p = la->next;
		q = lb->next;
	}
	else {
		k = lenB - lenA;
		p = lb->next;
		q = la->next;
	}
	while (k--) {
		p = p->next;//让p向前移动k位
	}
	while (p != null) {
		if (p == q)//若p==q,则找到公共结点
			return p;
		else {//若不等，则同步向后移动（同时抵达表尾）
			p = p->next;
			q = q->next;
		}
	}
	return 0;
}

时间复杂度：O(la+lb)

 

 算法思想：

不断使用尾插法，依次生成链表a,b

 

 

linklist create(linklist& A) {
	int i = 0;
	LNode B = (linklist)malloc(sizeof(LNode));
	LNode* ra=A, * rb = B;
	p = A->next;
	A->next = null;
	while (p != null) {
		if (i % 2) {//若是奇数插入a表
			ra->next = p;
			ra = p;
		}
		else {//若是偶数，插入b表
			rb->next = p;
			rb = p;
		}
		i++;
		p = p->next;
	}
	ra->next = null;
	rb->next = null;
	return B;
}