排序算法
排序的定义:
整理表中的元素,使之按关键字递增或者递减有序排列
排序的稳定性
如果待排序的列表中存在多个关键字相同的元素,经过排序后这些元素之间的相对次序不变,这种排序算法就是稳定的

两个9经过排序后位置不变,这个算法是稳定的
内排序和外排序
排序时不涉及数据的内外存交换,元素个数少--内排序
反之是外排序
性能
最好的算法时间复杂度:O(nlog2n)
比如:堆排序、二路归并排序、快速排序``
数据结构
typedef int KeyType;
typedef struct
{
KeyType key;
infoType data;
}RecType;
1.插入排序
有直接插入排序、折半插入排序、希尔排序
直接插入排序
思路:
待排序的元素放在a[0....n-1]中,a被划分成a[0...i-1],a[i....n-1]
前一个是排好序的有序区,后面的是无序区,初始时i=1,有序区是只有a[0];
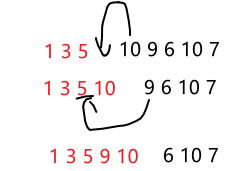
将无序区的开头元素a[i]插入到有序区[0....i-1]中的适当位置,使之成为a[0.....i]的有序区
这种方法将增量法,因为每次都使有序区增加一个元素
如何将a[i]插入到有序区中?(第i趟排序)
先将a[i]暂放到temp中,j在有序表中从后向前查找,关键字大于tmp的均后移一个位置。若找到小于或者等于temp的,将temp放在它后面。
算法实现
点击查看代码
typedef int KeyType;
typedef struct
{
KeyType key;
infoType data;//记录的其他数据项
}RecType;
void InsertSort(RecType a[], int n)
{
int i, j, RecType temp;
for (i = 1; i < n; i++)
{
if (a[i].key < a[i - 1].key) {
temp = a[i];
j = i - 1;
do {
a[j + 1] = a[j];//比temp大的往后移动一个位置
j--;//指针向前移动一个位
} while (j >= 0 && a[j].key > temp.key);
a[j + 1] = temp;//找到比它小或者相等的,放在其后面
}
}
}
算法分析
初始数据有序:
比较次数:n-1;
移动次数:0;
初始数据为反序:
比较次数:nn;
(1+2+3+.....n-1)=(n-1+1)(n-1)/2=O(n^2)
移动次数:nn;
(一趟移动a[0....i-1] 移动i次 还有temp=a[i] a[j+1]=temp的移动两次 共i+2次)=3+4+....n+1=(3+n+1)(n+1-2)/2=(n+4)*(n-1)/2
平均情况下:
a[0...i-1]有i个元素,
比较次数:i/2;
移动次数:i/2+2;
两者:i/2+i/2+2=i+2(1<=i<=n-1)=(n+1-2)*(n+1+3)/2=O(n^2)
直接插入排序只使用了i,j,temp辅助变量,所以空间复杂度为o(1)
因为关键字小于等于temp的,将temp插在其后面,所以关键字相同的记录相对次序不变,算法是稳定的
折半插入排序
思路:
有序区是有序的,可先采用折半查找方法在a[0...i-1]中找到插入位置,再移动元素插入
第i趟:
a【low...high】(low=0,high=i-1)
折半查找插入a[i]的位置为a【high+1】,再将a[high+1..i-1]元素后移一位,然后a[high+1]=a[i];
点击查看代码
typedef int KeyType;
typedef struct
{
KeyType key;
infoType data;//记录的其他数据项
}RecType;
void BinInsertSort(RecType a[], int n) {
int i, j, low, high, mid;
RecType temp;
for (i = 1; i < n; i++) {
if (a[i].key < a[i - 1].key) {
temp = a[i];
low = 0;
high = i - 1;
while (low <= high) {
mid = (low + high) / 2;
if (temp.key < a[mid].key)
high = mid - 1;
else
low = mid + 1;
}//找位置high
for (j = i - 1; j >= high + 1; j--)//集中移动
a[j + 1] = a[j];
a[high + 1] = temp;
}
}
}
算法分析
与直接插入不同的是一个是分散移动,一个是集中移动
折半查找的平均比较次数:
log2(i+1)-1
平均移动:i/2+2;
平均:log2(i+1)-1+i/2+2=O(n^2)
和直接插入排序相比,仅仅减少关键字的比较次数,性能不咋地,且空间复杂度:O(1),也是比较稳定的
希尔排序
思路:
分组插入方法。
取<n的整数d作为第一个增量,把表分成d个组,将所有距离为d的倍数的元素放在同一组,在各组内进行直接插入排序;
然后取d2(<d)重复上述分组和排序,直到dn=1...即所有元素直接插入排序
六分钟视频链接:
https://www.bilibili.com/video/BV1rE411g7rW/?spm_id_from=333.337.search-card.all.click&vd_source=bfaaef27306ec641467155b6686ff096
算法实现:
点击查看代码
void ShellSort(RecType a[], int n) {
int i, j, d;
RecType temp;
d = n / 2;
while (d > 0) {
for (i = d; i < n; i++) {
temp = a[i];
j = i - d;
while (j >= 0 && temp.key < a[j].key) {
a[j + d] = a[j];
j = j - d;
}
a[j + d] = temp;
}
d = d / 2;
}
}
2.交换排序
基本思想:两两比较元素的关键字,次序相反就交换,直到没有反序的元素为止。
有两种:冒泡排序和快速排序
冒泡排序
思路:
通过无序区相邻元素比较,交换使最小的元素往前面移动。
从最下面的元素开始,煤两个相邻关键字进行比较,使得一趟之后,最小的元素达到最上端,以此类推。
算法实现:
点击查看代码
void BubbleSort(RecType a[], int n) {
int i, j;
for (i = 0; i < n - 1; i++) {
for (j = n - 1; j > i; j--) {
if (a[j].key < a[j - 1].key) {
RecType temp;
temp = a[j];
a[j] = a[j - 1];
a[j - 1] = temp;
}
}
}
}
如果某一趟比较时不出现元素交换动作,说明可以结束算法,改进之后:
点击查看代码
void BubbleSort(RecType a[], int n) {
int i, j;
bool exchange = false;
for (i = 0; i < n - 1; i++) {
for (j = n - 1; j > i; j--) {
if (a[j].key < a[j - 1].key) {
RecType temp;
temp = a[j];
a[j] = a[j - 1];
a[j - 1] = temp;
exchange = true;
}
}
if (!exchange)
return;
}
}
改进前的算法:
初始数据是正序
比较:n-1;
移动:0
初始数据是反序
比较:n-1+n-2+....+1=n(n-1)/2=O(n^2)
移动:3n*(n-1)/2=O(n^2)
平均情况下,因为算法会在中间的某一道排序后终止,但证明平均的趟数是O(n),由此得出比较次数仍是O(n^2)
比直接插入排序的性能还低,只用了三个辅助变量,空间复杂度为o(1),当两个元素关键字相等时,相对位置不变,是一个稳定的算法
快速排序
思路:
由冒泡改进,在待排序区取一个元素作为基准,以此分为两部分,比它小的放它前面,大的放它后面,对这产生的两部分重复上述过程,,直到每一部分只有一个元素或空为止。
算法实现:
点击查看代码
int partition(RecType a[], int s, int t) {
int i = s, j = t;
RecType temp = a[i];
while (i < j) {
while (j > i && a[j].key >= temp.key)
j--;
a[i] = a[j];
while (j > i && a[i].key <= temp.key)
i++;
a[j] = a[i];
}
a[i] = temp;
return i;
}
void QuickSort(RecType a[], int s, int t) {
int i;
if (s < t) {
i = partition(a, s, t);
QuickSort(a, s, i - 1);
QuickSort(a, i + 1, t);
}
}
算法分析:
最好情况是:每次选的基准是当前表的中值,每次划分的两部分都长度相等,这样递归树高度为log2(N)每次划分时间:O(n)
时间复杂度:O(nlog2(n))
空间复杂度:O(log2(n))
最坏情况是:每次基准是当前表的最小值,左子区为空,右为n-1个元素,递归树高度:n,需要n-1次划分
时间复杂度:O(n^2)
空间复杂度:O(n)
平均复杂度:n*log2(n),空间复杂度:log2(n)
正反序都是最坏情况,最好的是每次都划分为两个相等的子区间。
该算法是不稳定的算法
选择排序
基本思想:每一趟从待排序的元素中选最小的,放在排好的表最后,直到全部排完。
简单选择排序
基本思路:
第i趟:0<=i<n-1
有序区:a[0...i-1]
无序区:a[i..n-1]
无序区选最小:a[k]
将a[k]和无序区第一个交换,a[0...i],a[i+1,...n-1]成为新的有序区和无序区
n-1趟a[0...n-1]为有序表
算法实现
点击查看代码
typedef int KeyType;
typedef struct {
KeyType key;
infoType data;
}RecType;
void SelectSort(RecType a[], int n) {
int i, j, k;
for (i = 0; i < n - 1; i++) {
k = i;
for (j = i + 1; j < n; j++) {
if (a[j].key < a[k].key) {
k = j;
}
if (k != i) {
RecType temp;
temp = a[j];
a[j] = a[k];
a[k] = temp;
}
}
}
}
算法分析
内循环:(n-1)-(i+1)+1=n-i-1次比较
外循环:0...n-2--n-1次
总比较次数:n-1+n-2+....+1=n*(n-1)/2=0(n^2)
表为正序时:移动次数为0
表为反序:移动次数:3(n-1)
无论什么序列,比较平均时间复杂度:O(n^2)
简单选择排序算法的使用i,j,k,temp四个辅助变量,空间复杂度:O(1)
是不稳定的算法
比如5,3,2,5,1,7
第一趟,把5和5的相对位置改变了
堆排序
思路:
树形选择排序方法
将a[1...n]看成一棵完全二叉树的顺序存储结构,利用双亲结点和孩子结点之间的位置关系在无序区中选择关键字最大(最小)的元素
堆的定义:a[1..n]中的n个关键字序列k1,k2,k3....kn称为堆,满足以下性质:
ki<=k2i且ki<=k2i+1 或者 ki>=k2i且k>=k2i+1(1<=i<=[n/2]下取整)
第一种小根堆,第二种大根堆
下面讨论大根堆:
堆排序和选择排序差不多,挑选最大最小时方法不同
用筛选法实现:
完全二叉树根结点:a[i],左右子树是大根堆,将a[2i]和a[2i+1]与a[i]的比较,a[i]较小,与最大交换。
筛选算法实现
必须以low为根节点的左右子树是大根堆
创建初始堆a[1...n],从i=[n/2]下取整~1,大的浮上来,小的沉下去。由于最后是a[1]为最大,所以把它与最后叶子结点交换,最大元素已排,整个待排序队伍少一个,根节点改变,n-1不一定为堆,但左右子树均为堆,再调用sift算法,a[1...n-1]调整成堆,根节点为次大,将其放到倒二位置,堆中根与最后一个叶子交换,待排变n-2,如此,直到完全二叉树变成值剩一个根位置。
点击查看代码
void sift(RecType a[], int low,int high) {
int i = low, j = 2 * i;
RecType temp = a[i];
while (j <= high) {
if (j < high && a[j].key < a[j + 1].key)
j++;
if (temp.key < a[j].key) {
a[i] = a[j];
i = j;
j = 2 * i;
}
else break;
}
a[i] = temp;
}
void HeapSort(RecType a[], int n) {
int i;
for (i = n / 2; i >= 1; i--)//初始化堆
sift(a, i, n);
for (i = n; i >= 2; i--)
{
RecType temp;
temp = a[i];
a[i] = a[1];
a[1] = temp;
sift(a, 1, i - 1);//对a[1...i-1]进行筛选,得到i-1个结点的堆;
}
}
算法分析
时间主要由建立初始堆和反复建堆构成,均是通过调用sift函数实现
对于高度为k,调用sift函数,while循环最多执行k-1次,2(k-1)次比较, k+1次移动,主要以关键字比较来分析时间复杂度
n个结点的完全二叉树高度h=[log2N]下取整+1
初始化堆:
调整的层:h-1~1
第i层高度:h-i+1
第i层结点最多:2^(i-1)
比较次数:2^(i-1)*2(h-i+1 -1)(1<=i<=h-1)= 2^i *(h-i)= 2^h-1 *1 +2^h-2 2+....2(h-1)=2^(h+1) - 2h-2
< 2 ^ [ log2 N ]+2 < 4* 2^log2N =4n
重复建堆的关键字比较:< 2nLog2(N)
最坏时间复杂度:4n+nLog2(N)=O(nlog2(N))
不适合元素较少的排序表,只使用了i,j,temp所以空间复杂度为:O(1)
不稳定的排序
归并排序
思路:
将两个或两个以上的有序表合成一个有序表
最简单的叫二路归并(两个表)
基本思路:将a[0...n-1]看作n个长度为1的有序序列,两两归并,得到上取整【n-2】个长度为2的有序序列,再两两归并。。。直到得到长度为n的有序序列
两有序表归并成一个有序表的算法Merge()
a[low...mid] a[mid+1..high]先将其合并到一个暂存的数组中a1,合并完后将a1复制到a
每次从两个段中取出一个元素进行关键字的比较,较小的放a1,各段余下的全部复制到a1中。这样a1是一个有序表,再复制到a中
算法实现
点击查看代码
void Merge(RecType a[], int low, int mid, int high) {
RecType* a1;
int i = low, j = mid + 1, k = 0;//k是a1的下标,i,j分别是第一段,第二段的下标
a1 = (RecType*)malloc((high - low + 1) * sizeof(RecType)); //动态分配空间
while (i <= mid && j <= high) {//第一段和第二段未扫描完时循环
if (a[i].key <= a[j].key)//第一段的元素放入a1中
{
a1[k] = a[i];
i++;
k++;
}
else {//第二段的元素放入a1
a1[k] = a[j];
j++;
k++;
}
}
while (i <= mid) {//将第一段的余下部分复制到a1
a1[k] = a[i];
i++;
k++;
}
while (j <= high) {
a1[k] = a[j];
j++;
k++;
}
for (k = 0, i = low; i <= high; i++, k++)//a1复制到a[low,high]
a[i] = a1[k];
free(a1);
}
Merge实现了一次归并,辅助空间是要归并的元素个数,Merge来解决一趟归并问题。
某趟:
各子表长度length,a[0...n-1]中共上取整【n/length】个有序子表;
a[0...length-1] ||| a[length....2*length-1]....
有两个特殊情况:表的个数可能为奇数||最后一个子表的长度小于length
解决方法:最后一个子表无需和其他子表归并,子表个数为偶数,注意最后一对子表中后一个子表的区间上界:n-1
一趟归并:
点击查看代码
void MergePass(RecType a[], int length, int n)
{
int i;
for (i = 0; i + 2 * length - 1 < n; i = i + 2 * length)//归并length长的两相邻子表
Merge(a, i, i + length - 1, i + 2 * length - 1);
if (i + length - 1 < n - 1) {//余下两个子表,后者长度小于length
Merge(a, i, i + length - 1, n - 1);//归并这两个子表
}
}
总趟数为:上取整:log2(N)
二路归并排序算法实现:
点击查看代码
void MergeSort(RecType a[], int n) {
int length;
for (length = 1; length < n; length = 2 * length) {//log2(n)趟排序
MergePass(a, length, n);
}
}
算法分析
趟数:log2(n) 每趟时间为O(n),最好最坏时间复杂度为:nlog2(n),平均也是
总的辅助空间复杂度:O(n)
是一种稳定的排序算法
基数排序
思路:
通过分配和收集过程来实现排序,不需要进行关键字的比较。
元素a[i].key是由多个数字组成,k^(d-1), k^(d-2).......每一位都在[0,r)范围内,r是基数。
基数排序有两种,最低位优先,最高位优先。主要讨论前者
最低位优先过程:
先按最低位的值对元素进行排序,再排较低位。。。。类推
由低位向高位,每趟都是根据关键字的一位并在前一趟的基础上对所有元素进行排序,直到最高位。
排序过程:
分配:使用Q1.。。。。Qr-1 这些队列置空,考察每个元素,如果元素aj的关键字k^i=k,就把元素插入Qk队列
收集:将Q0.....Qr-1各个队列的元素依次首尾相接,得到新元素序列,从而组成新的线性表
算法实现:
点击查看代码
typedef struct node {
char data[MAXD];//MAXD为最大的关键字位数
struct node* next;
}NodeType;
void RadixSort(NodeType*& p, int r, int d) {//LSD基数排序算法
NodeType* head[MAXD], * tail[MAXD], * t;//定义各个链队收尾指针
int i, j, k;
for (i = 0; i <= d - 1; i++)//低位到高位循环
{
for (j = 0; j < r; j++)//初始化各个链队的收尾指针
head[j] = tail[j] = NULL;
while (p != NULL)//分配:对于原链表中的每个结点循环
{
k = p->data[i] - '0';//找第k个链队
if (head[k] == NULL) {//第k个链队空时,队头队尾均指向p
head[k] = p;
tail[k] = p;
}
else {//第k个链队非空时结点p进队
tail[k]->next = p;
tail[k] = p;
}
p = p->next;
}
p = NULL;//重新用p来收集所有结点
for(j=0;j<r;j++)//收集:对于每一个链队循环
if (head[j] != NULL) {//若第j个链队是第一个非空链队
if (p == NULL) {
p = head[j];
t = tail[j];
}
else {//若第j个链队是其他非空链队
t->next = head[j];
t = tail[j];
}
}
t->next = NULL;//最后一个结点next域置为NULL
}
}
算法分析
共进行d趟的分配和收集,分配需要扫描所有结点,收集是按队列进行的 一趟:O(n+r)
时间复杂度:O(d(n+r))
需要辅助空间:r(r个队列) 空间复杂度:O(r)
是一种稳定的排序算法



 浙公网安备 33010602011771号
浙公网安备 33010602011771号