一、平面点集 *\(n\) 维空间

1.平面点集

由平面解析几何知道，当在平面上引入了一个平面直角坐标系后，平面上的点 \(P\) 与有序二元实数组 \((x, y)\) 之间就建立了一一对应。于是，我们常把有序实数组 \((x, y)\) 与平面上的点 \(P\) 视作是等同的。这种建立了坐标系的平面称为坐标平面。二元有序实数组 \((x, y)\) 的全体，即 \(\mathbb{R}^2 = \mathbb{R} \times \mathbb{R} = \{ (x, y) | x, y \in \mathbb{R} \}\) 就表示坐标平面。

坐标平面上具有某种性质 \(P\) 的点的集合，称为平面点集，记作

例如，平面上以原点为中心、\(r\) 为半径的圆内所有的点的集合是

如果以点 \(P\) 表示 \((x, y)\) ，\(|OP|\) 表示点 \(P\) 到原点 \(O\) 的距离，那么集合 \(C\) 也可以表成

现在引入 \(\mathbb{R}^2\) 中邻域的概念。

设 \(P_0 (x_0, y_0)\) 是 \(xOy\) 平面上的一个点，\(\delta\) 是某一正数。与点 \(P_0 (x_0, y_0)\) 距离小于 \(\delta\) 的点 \(P(x, y)\) 的全体，称为点 \(P_0\) 的 \(\delta\) 邻域 ，记作 \(U(P_0, \delta)\) ，即

也就是

点 \(P_0\) 的去心 \(\delta\) 邻域，记作 \(\mathring{U} (P_0, \delta)\) ，即

在几何上，\(U(P_0, \delta)\) 就是 \(xOy\) 平面上以点 \(P_0(x_0, y_0)\) 为中心、\(\delta > 0\) 为半径的圆内部的点 \(P(x, y)\) 的全体。

如果不需要强调领域的半径 \(\delta\) ，则用 \(U(P_0)\) 表示点 \(P_0\) 的某个邻域，点 \(P_0\) 的去心邻域记作 \(\mathring{U}(P_0)\) 。

利用邻域来描述点和点集之间的关系。

任意一点 \(P \in \mathbb{R}^2\) 与任意一个点集 \(E \subset \mathbb{R}^2\) 之间必有一下三种关系中的一种：

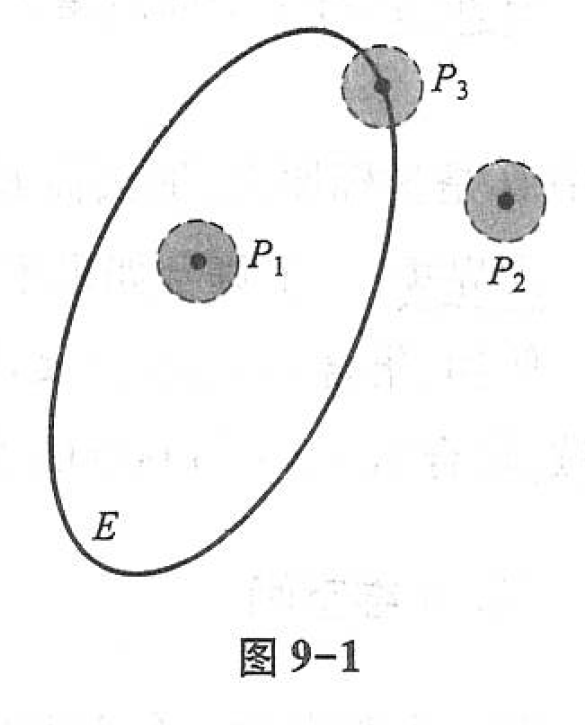
（1）内点 ：如果存在点 \(P\) 的某个邻域 \(U(P)\) ，使得 \(U(P) \subset E\) ，那么称 \(P\) 为 \(E\) 的内点（如图9-1中，\(P_1\) 为 \(E\) 的内点）；

（2）外点 ：如果存在点 \(P\) 的某个邻域 \(U(P)\) ，使得 \(U(P) \cap E = \varnothing\) ，那么称 \(P\) 为 \(E\) 的外点（如图9-1中，\(P_2\) 为 \(E\) 的外点）；

（3）边界点 ：如果点 \(P\) 的任一邻域内既含有属于 \(E\) 的点，又含有不属于 \(E\) 的点，那么称 \(P\) 为 \(E\) 的边界点（如图9-1中，\(P_3\) 为 \(E\) 的边界点）。

\(E\) 的边界点的全体，称为 \(E\) 的 边界 ，记作 \(\partial E\) 。

\(E\) 的内点必属于 \(E\) ；\(E\) 的外点必定不属于 \(E\) ；而 \(E\) 的边界点可能属于 \(E\) ，也可能不属于 \(E\) 。

任意一点 \(P\) 与一个点集 \(E\) 之间除了上述三种关系之外，还有另外一种关系，这就是聚点。

聚点 ：如果对于任意给定的 \(\delta > 0\) ，点 \(P\) 的去心邻域 \(\mathring{U}(P, \delta)\) 内总有 \(E\) 中的点，那么称 \(P\) 是 \(E\) 的 聚点 。

由聚点的定义可知，点集 \(E\) 的聚点 \(P\) 本身，可以属于 \(E\) ，也可以不属于 \(E\) 。

例如，设平面点集

满足 \(1 < x^2 + y^2 < 2\) 的一切点 \((x, y)\) 都是 \(E\) 的内点；满足 \(x^2 + y^2 = 1\) 的一切点 \((x, y)\) 都是 \(E\) 的边界点，它们都不属于 \(E\) ；满足 \(x^2 + y^2 = 2\) 的一切点 \((x, y)\) 也是 \(E\) 的边界点，它们都属于 \(E\) ；点集 \(E\) 以及它的边界 \(\partial E\) 上的一切点都是 \(E\) 的聚点。

根据点集所属点的特征，再来定义一些重要的平面点集。

开集 ：如果点集 \(E\) 的点都是 \(E\) 的内点，那么称 \(E\) 为开集。

闭集 ：如果点集 \(E\) 的边界 \(\partial E \subset E\) ，那么称 \(E\) 为闭集。

例如，集合 \(\{ (x, y) | 1 < x^2 + y^2 < 2 \}\) 是开集；集合 \(\{ (x, y) | 1 \leqslant x^2 + y^2 \leqslant 2 \}\) 是闭集；而集合 \(\{ (x, y) | 1 < x^2 + y^2 \leqslant 2 \}\) 既非开集，也非闭集。

连通集 ：如果点集 \(E\) 内任何两点，都可用折线连接起来，且该折线上的点都属于 \(E\) ，那么称 \(E\) 为连通集。

区域 （或 开区域）：连通的开集称为区域或开区域。

闭区域 ：开区域连同它的边界一起所构成的点集称为闭区域。

例如，集合 \(\{ (x, y) | 1 < x^2 + y^2 < 2 \}\) 是区域，而集合 \(\{ (x, y) | 1 \leqslant x^2 + y^2 \leqslant 2 \}\) 是闭区域。

有界集 ：对于平面点集 \(E\) ，如果存在某一正数 \(r\) ，使得

其中 \(O\) 是坐标原点，那么称 \(E\) 为有界集。

无界集 ：一个集合如果不是有界集，就成这个集合为无界集。

例如，集合 \(\{ (x, y) | 1 \leqslant x^2 + y^2 \leqslant 2 \}\) 是有界闭区域，集合 \(\{ (x, y) | x + y > 0 \}\) 是无界开区域，集合 \(\{ (x, y) | x + y \geqslant 0 \}\) 是无界闭区域。

*2. \(n\) 维空间

设 \(n\) 为取定的一个正整数，我们用 \(\mathbb{R}^n\) 表示 \(n\) 元有序实数组 \((x_1, x_2, \cdots, x_n)\) 的全体所构成的集合，即

\(\mathbb{R}^n\) 中的元素 \((x_1, x_2, \cdots, x_n)\) 有时也用单个字母 \(\boldsymbol{x}\) 来表示，即 \(\boldsymbol{x} = (x_1, x_2, \cdots, x_n)\) .当所有的 \(x_i(i = 1, 2, \cdots, n)\) 都为零时，称这样的元素为 \(\mathbb{R}^2\) 中的零元，记为 \(\boldsymbol{0}\) 或 \(O\) 。在解析几何中，通过直角坐标系，\(\mathbb{R}^2\) （或 \(\mathbb{R}^3\)）中的元素分别与平面（或空间）中的点或向量建立一一对应，因而 \(\mathbb{R}^n\) 中的元素 \(\boldsymbol{x} = (x_1, x_2, \cdots, x_n)\) 也称为 \(\mathbb{R}^n\) 中的一个点或一个 \(n\) 维向量，\(x_i\) 称为点 \(x\) 的第 \(i\) 个坐标或 \(n\) 维向量 \(\boldsymbol{x}\) 的第 \(i\) 个分量。特别地，\(\mathbb{R}^2\) 中的零元 \(\boldsymbol{0}\) 称为 \(\mathbb{R}^n\) 中的坐标原点或 \(n\) 维零向量。

为了在集合 \(\mathbb{R}^n\) 中的元素之间建立联系，在 \(\mathbb{R}^n\) 中定义线性运算如下：

设 \(\boldsymbol{x} = (x_1, x_2, \cdots, x_n)\) ，\(\boldsymbol{y} = (y_1, y_2, \cdots, y_n)\) 为 \(\mathbb{R}^n\) 中的任意两个元素，\(\lambda \in \mathbb{R}\) ，规定

这样定义了线性运算的集合 \(\mathbb{R}^n\) 称为 \(n\) 维空间。

\(\mathbb{R}^n\) 中的点 \(\boldsymbol{x} = (x_1, x_2, \cdots, x_n)\) 和点 \(\boldsymbol{y} = (y_1, y_2, \cdots, y_n)\) 间的距离，记作 \(\rho(\boldsymbol{x}, \boldsymbol{y})\) ，规定

显然，\(n = 1, 2, 3\) 时，上述规定与数轴上、直角坐标系下平面及空间中两点间的距离一致。

\(\mathbb{R}^n\) 中元素 \(\boldsymbol{x} = (x_1, x_2, \cdots, x_n)\) 与零元 \(\boldsymbol{0}\) 之间的距离 \(\rho (\boldsymbol{x}, \boldsymbol{0})\) 记作 \(\| \boldsymbol{x} \|\) （在 \(\mathbb{R}^1, \mathbb{R}^2, \mathbb{R}^3\) 中，通常将 \(\| \boldsymbol{x} \|\) 记作 \(|\boldsymbol{x}|\)），即

采用这一记号，结合向量的线性运算，便得

在 \(n\) 维空间 \(\mathbb{R}^n\) 中定义了距离以后，就可以定义 \(\mathbb{R}^n\) 的变元的极限：

设 \(\boldsymbol{x} = (x_!, x_2, \cdots, x_n) , \boldsymbol{a} = (a_1, a_2, \cdots, a_n) \in \mathbb{R}^n\) 。如果

那么称变元 \(\boldsymbol{x}\) 在 \(\mathbb{R}^n\) 中趋于固定元 \(\boldsymbol{a}\) ，记作 \(\boldsymbol{x} \to \boldsymbol{a}\) 。

显然，

在 \(\mathbb{R}^2\) 中引入线性运算和距离，使得有关平面点集的一些列概念，可以方便地引入到 \(n(n \geqslant 3)\) 维空间中来。例如，

设 \(\boldsymbol{a} = (a_1, a_2, \cdots, a_n) \in \mathbb{R}^n\) ，\(\delta\) 是某一正数，则 \(n\) 维空间内的点集

就定义为 \(\mathbb{R}^n\) 中点 \(\boldsymbol{a}\) 的 \(\delta\) 邻域。以邻域为基础，可以定义点集的内点、外点、边界点和聚点以及开集、闭集、区域等一系列概念。

二、多元函数的概念

定义1 设 \(D\) 是 \(\mathbb{R}^2\) 上的一个非空子集，称映射 \(f:D \to \mathbb{R}\) 为定义在 \(D\) 上的 二元函数 ，通常记为

或

其中点集 \(D\) 称为该函数的 定义域 ，\(x\) 和 \(y\) 称为 自变量 ，\(z\) 称为 因变量 。

上述定义中，与自变量 \({x}\) 和 \({y}\) 的一对值（即二元有序实数组）\({(x, y)}\) 相对应的因变量 \({z}\) 的值，也称为 \({f}\) 在点 \({(x, y)}\) 处的函数值，记作 \({f(x, y)}\) ，即 \({z=f(x, y)}\) ．函数值 \({f(x, y)}\) 的全体所构成的集合称为函数 \({f}\) 的值域，记作 \({f(D)}\) ，即

与一元函数的情形相仿，记号 \({f}\) 与 \({f(x, y)}\) 的意义是有区别的，但习惯上常用记号 ＂\({f(x, y),(x, y) \in D}\)＂或＂\({z=f(x, y),(x, y) \in D}\)＂来表示 \({D}\) 上的二元函数 \({f}\) ．表示二元函数的记号 \({f}\) 也是可以任意选取的，例如也可以记为 \({z=\varphi(x, y), z=z(x, y)}\) 等．

类似地，可以定义三元函数 \({u=f(x, y, z),(x, y, z) \in D}\) 以及三元以上的函数．一般地，把定义 1 中的平面点集 \({D}\) 换成 \({n}\) 维空间 \({\mathbb{R}^{n}}\) 内的点集 \({D}\) ，映射 \({f: D \rightarrow \mathbb{R}}\) 就称为定义在 \({D}\) 上的 \({n}\) 元函数，通常记为

或简记为

也可记为

当 \({n=2}\) 或 \({n=3}\) 时，习惯上将点 \({\left(x_{1}, x_{2}\right)}\) 与点 \({\left(x_{1}, x_{2}, x_{3}\right)}\) 分别写成 \({(x, y)}\) 与 \({(x, y, z)}\) ．这时，若用字母表示 \({\mathbb{R}^{2}}\) 或 \({\mathbb{R}^{3}}\) 中的点，即写成 \({P(x, y)}\) 或 \({M(x, y, z)}\) ，则相应的二元函数及三元函数也可简记为 \({z=f(P)}\) 及 \({u=f(M)}\) ．

当 \({n=1}\) 时，\({n}\) 元函数就是一元函数；当 \({n \geqslant 2}\) 时，\({n}\) 元函数统称为多元函数．

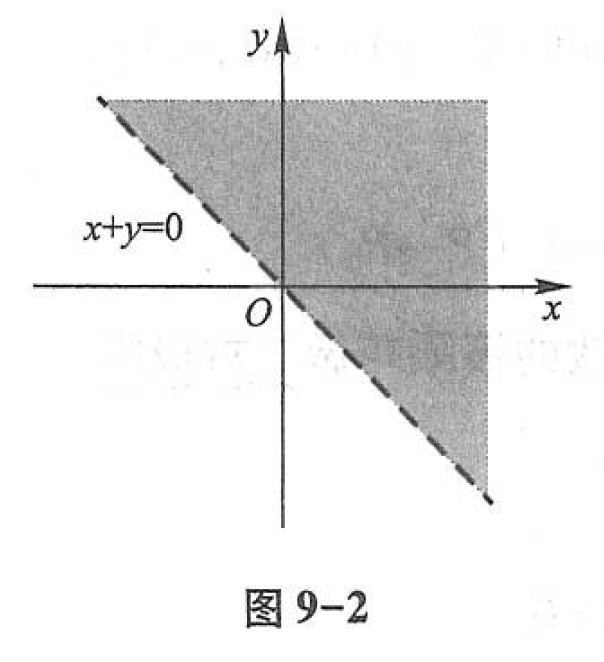
关于多元函数的定义域，与一元函数相类似，我们作如下约定：在一般地讨论用算式表达的多元函数 \({u=f(x)}\) 时，就以使这个算式有意义的变元 \({x}\) 的值所组成的点集为这个 多元函数的自然定义域 。因而，对这类函数，它的定义域不再特别标出。例如，函数 \({z=\ln (x+y)}\) 的定义域为

（图 9－2），这是一个无界开区域．

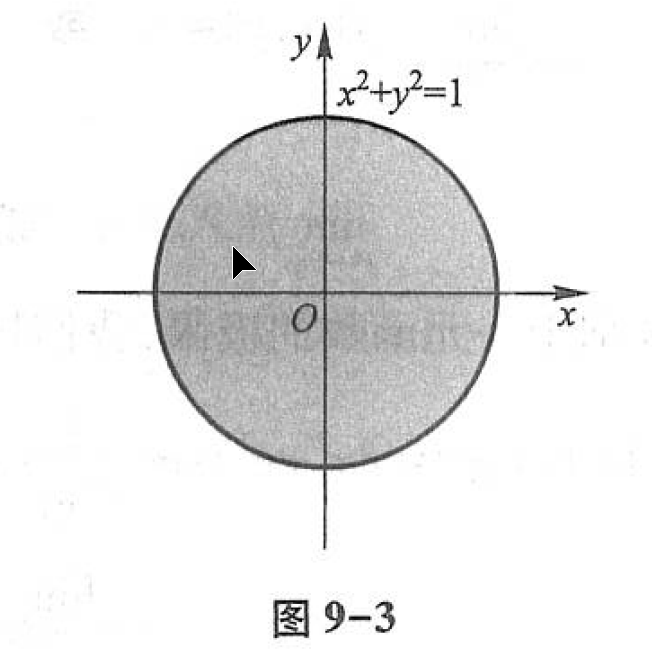
又如，函数 \({z=\arcsin \left(x^{2}+y^{2}\right)}\) 的定义域为

（图9－3），这是一个有界闭区域．

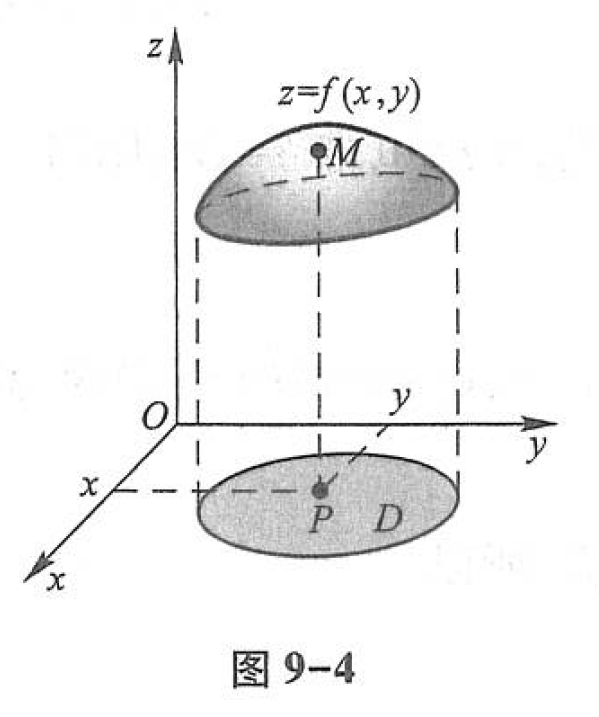
设函数 $ z=f(x, y) $ 的定义域为 \(D\) ．对于任意取定的点 \(P(x, y) \in D\) ，对应的函数值为 $ z=f(x, y) $ ．这样，以 \(x\) 为横坐标、 \(y\) 为纵坐标和 $ z=f(x, y) $ 为竖坐标在空间就确定一点 \(M(x, y, z)\) ．当 \((x, y)\) 遍取 \(D\)上的一切点时，得到一个空间点集

这个点集称为 二元函数 $ z=f(x, y) $ 的图形 （图9－4）．通常我们也说二元函数的图形是一张曲面．

例如，由空间解析几何知道，线性函数 \(z=a x+b y+c\)的图形是一张平面，而函数 \(z=x^{2}+y^{2}\) 的图形是旋转抛物面．

三、多元函数的极限

先讨论二元函数 \(z=f(x, y)\) 当 \((x, y) \rightarrow\left(x_{0}, y_{0}\right)\) ，即 \(P(x, y) \rightarrow P_{0}\left(x_{0}, y_{0}\right)\) 时的极限．
这里 \(P \rightarrow P_{0}\) 表示点 \(P\) 以任何方式趋于点 \(P_{0}\) ，也就是点 \(P\) 与点 \(P_{0}\) 间的距离趋于零，即

与一元函数的极限概念类似，如果在 \(P(x, y) \rightarrow P_{0}\left(x_{0}, y_{0}\right)\) 的过程中，对应的函数值 $ f(x, y) $ 无限接近于一个确定的常数 \(A\) ，那么就说 \(A\) 是函数 $ f(x, y) $ 当 \((x, y) \rightarrow \left(x_{0}, y_{0}\right)\) 时的极限．下面用＂\(\varepsilon-\delta\)＂语言描述这个极限概念．

定义 2 设二元函数 \(f(P)=f(x, y)\) 的定义域为 \(D, P_{0}\left(x_{0}, y_{0}\right)\) 是 \(D\) 的聚点．如果存在常数 \(A\) ，对于任意给定的正数 \(\varepsilon\) ，总存在正数 \(\delta\) ，使得当点 \(P(x, y) \in D \cap \stackrel{\circ}{U}\left(P_{0}, \delta\right)\) 时，都有

成立，那么就称常数 \(A\) 为函数 \(f(x, y)\) 当 \((x, y) \rightarrow\left(x_{0}, y_{0}\right)\) 时的极限，记作

也记作

为了区别于一元函数的极限，我们把二元函数的极限叫做 二重极限 。

必须注意，所谓二重极限存在，是指 \(P(x, y)\) 以任何方式趋于 \(P_{0}\left(x_{0}, y_{0}\right)\) 时， $ f(x, y) $ 都无限接近于 \(A\) 。因此，如果 \(P(x, y)\) 以某一特殊方式，例如沿着一条定直线或定曲线趋于 \(P_{0}\left(x_{0}, y_{0}\right)\) 时，即使 $ f(x, y) $ 无限接近于某一确定值，我们还不能由此断定函数的极限存在．但是反过来，如果当 \(P(x, y)\) 以不同的方式趋于 \(P_{0}\left(x_{0}, y_{0}\right)\) 时， $ f(x, y) $ 趋于不同的值，那么就可以断定这函数的极限不存在．

以上关于二元函数的极限概念，可相应地推广到 \(n\) 元函数 \(u=f(P)\) ，即 \(u=f\left(x_{1}\right.\) ， \(\left.x_{2}, \cdots, x_{n}\right)\) 上去．

关于多元函数的极限运算，有与一元函数类似的运算法则．

四、多元函数的连续性

定义 3 设二元函数 \(f(P)=f(x, y)\) 的定义域为 \(D, P_{0}\left(x_{0}, y_{0}\right)\) 为 \(D\) 的聚点，且 \(P_{0} \in D\)．如果

那么称函数 $ f(x, y) $ 在点 \(P_{0}\left(x_{0}, y_{0}\right)\) 连续．
设函数 $ f(x, y) $ 在 \(D\) 上有定义，\(D\) 内的每一点都是函数定义域的聚点。如果函数 $ f(x, y) $ 在 \(D\) 的每一点都连续，那么就称函数 $ f(x, y) $ 在 \(D\) 上连续，或者称 $ f(x, y) $ 是 \(D\)上的 连续函数 ．

以上关于二元函数的连续性概念，可相应地推广到 \(n\) 元函数 \(f(P)\) 上去．

定义 4 设函数 $ f(x, y) $ 的定义域为 \(D, P_{0}\left(x_{0}, y_{0}\right)\) 是 \(D\) 的聚点．如果函数 $ f(x, y) $ 在点 \(P_{0}\left(x_{0}, y_{0}\right)\) 不连续，那么称 \(P_{0}\left(x_{0}, y_{0}\right)\) 为函数 $ f(x, y) $ 的间断点．

一切多元初等函数在其定义区域内是连续的。所谓 定义区域 是指包含在定义域内的区域或闭区域。

由多元初等函数的连续性，如果要求它在点 \(P_0\) 处的极限，而该点又在此函数的定义区域内，那么此极限值就是函数在该点的函数值，即

在有界闭区域上连续的多元函数具有如下性质：

性质1（有界性与最大值最小值定理） 在有界闭区域 \(D\) 上的多元连续函数，必定在 \(D\) 上有界，且能取得它的最大值和最小值．

性质1就是说，若 \(f(P)\) 在有界闭区域 \(D\) 上连续，则必定存在常数 \(M>0\) ，使得对一切 \(P \in D\) ，有 \(|f(P)| \leqslant M\) ；且存在 \(P_{1}, P_{2} \in D\) ，使得

性质2（介值定理） 在有界闭区域 \(D\) 上的多元连续函数必取得介于最大值和最小值之间的任何值．
＊性质3（一致连续性定理） 在有界闭区域 \(D\) 上的多元连续函数必定在 \(D\) 上 一致连续 ．

性质3就是说，若 \(f(P)\) 在有界闭区域 \(D\) 上连续，则对于任意给定的正数 \(\varepsilon\) ，总存在正数 \(\delta\) ，使得对于 \(D\) 上的任意两点 \(P_{1}, P_{2}\) ，只要当 \(\left|P_{1} P_{2}\right|<\delta\) 时，都有

成立．