高等数学 8.6 空间曲线及其方程

目录

一、空间曲线的一般方程

我们已经知道空间曲线可以看做两个曲面的交线。设

\[F(x, y, z) = 0 \quad 和 \quad G(x, y, z) = 0 \]

是两个曲面的方程，则方程组

\[\begin{equation*} \begin{cases} F(x, y, z) = 0, \\ G(x, y, z) = 0. \end{cases} \end{equation*} \tag{6-1} \]

就是这两个曲面的交线 \(C\) 的方程，方程组 \((6-1)\) 也叫做 空间曲线 \(C\) 的一般方程 。

8.6例1

8.6例2

二、空间曲线的参数方程

空间曲线 \(C\) 的方程除了一般方程之外，也可以用参数形式表示，只要将 \(C\) 上动点的坐标 \(x, y\) 和 \(z\) 表示为参数 \(t\) 的函数

\[\begin{equation*} \begin{cases} x = x(t), \\ y = y(t), \\ z = z(t). \end{cases} \end{equation*} \tag{6-2} \]

当给定 \(t = t_1\) 时，就得到曲线 \(C\) 上的一个点 \((x_1, y_1, z_1)\) ；随着 \(t\) 的变动便可得曲线 \(C\) 上的全部点。方程组 \((6-2)\) 叫做 空间曲线的参数方程 。

8.6例3

*曲面的参数方程

介绍一下曲面的参数方程。曲面的参数方程通常是含两个参数的方程，形如

\[\begin{equation*} \begin{cases} x = x(s, t), \\ y = y(s, t), \\ z = z(s, t). \end{cases} \end{equation*} \tag{6-3} \]

例如空间曲线 \(\Gamma\)

\[\begin{equation*} \begin{cases} x = \varphi(t), \\ y = \psi(t), \\ z = \omega(t). \end{cases} \quad (\alpha \leqslant t \leqslant \beta) \end{equation*} \]

绕 \(z\) 轴旋转，所得旋转曲面的方程为

\[\begin{equation*} \begin{cases} x = \sqrt{[\varphi (t)]^2 + [\psi (t)]^2} \cos \theta, \\ y = \sqrt{[\varphi (t)]^2 + [\psi (t)]^2} \sin \theta, \\ z = \omega (t). \end{cases} \quad \alpha \leqslant t \leqslant \beta, 0 \leqslant \theta \leqslant 2 \pi \end{equation*} \tag{6-4} \]

这是因为，固定一个 \(t\) ，得 \(\Gamma\) 上一点 \(M_1 (\varphi (t), \psi (t), \omega (t))\) ，点 \(M_1\) 绕 \(z\) 轴旋转，得空间的一个圆，该圆在平面 \(z = \omega (t)\) 上，其半径为点 \(M_1\) 到 \(z\) 轴的距离 \(\sqrt{[\varphi (t)]^2 + [\psi (t)]^2}\) ，因此，固定 \(t\) 的方程 \((6-4)\) 就是该圆的参数方程。再令 \(t\) 在 \([\alpha, \beta]\) 内变动，方程 \((6-4)\) 便是旋转曲面的方程。

例如直线

\[\begin{equation*} \begin{cases} x = 1, \\ y = t, \\ z = 2t. \end{cases} \end{equation*} \]

绕 \(z\) 轴旋转所得的旋转曲面（如图8-56）的方程为

\[\begin{equation*} \begin{cases} x = \sqrt{1+ t^2} \cos \theta, \\ y = \sqrt{1+ t^2} \sin \theta, \\ z = 2t. \end{cases} \end{equation*} \]

\(\left( 上式消去t和\theta ，得曲面的直角坐标方程为 x^2 + y^2 = 1 + \cfrac{z^2}{4} \right)\) 。

8.6图8-56

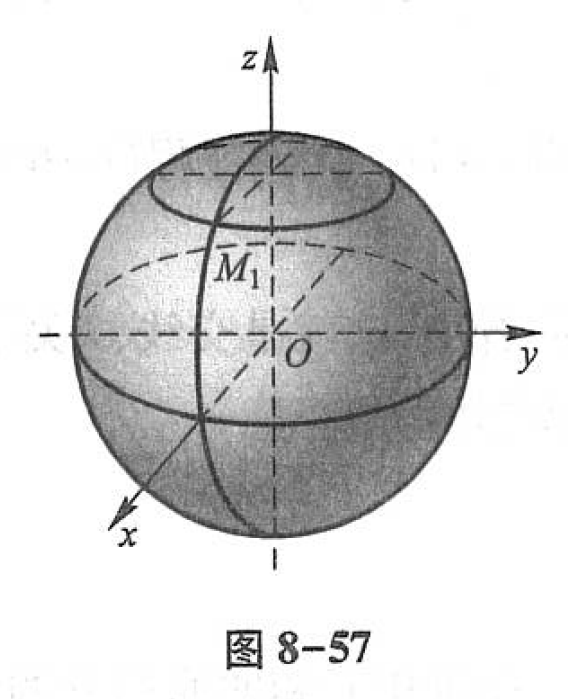
又如球面 \(x^2 + y^2 + z^2 = a^2\) 可以看成 \(zOx\) 面上的半圆周

\[\begin{equation*} \begin{cases} x = a \sin \varphi, \\ y = 0, \\ z = a \cos \varphi, \end{cases} \quad 0 \leqslant \varphi \leqslant \pi \end{equation*} \]

绕 \(z\) 轴旋转所得（图8-57），故球面方程为

\[\begin{equation*} \begin{cases} x = a \sin \varphi \cos \theta, \\ y = a \sin \varphi \sin \theta, \\ z = a \cos \varphi, \end{cases} \quad 0 \leqslant \varphi \leqslant \pi, 0 \leqslant \theta \leqslant 2 \pi. \end{equation*} \]

8.6图8-57

三、空间曲线在坐标平面上的投影

设空间曲线 \(C\) 的一般方程为 \((6-1)\) ，现在来研究由方程组 \((6-1)\) 消去变量 \(z\) 后（如果可能的话）所得的方程

\[H(x, y) = 0 \tag{6-5} \]

由于方程 \((6-5)\) 是由方程组 \((6-1)\) 消去 \(z\) 后所得的结果，因此当 \(x, y\) 和 \(z\) 满足方程组 \((6-1)\) 时，前两个坐标 \(x, y\) 必定满足方程 \((6-5)\) ，这说明曲线 \(C\) 上的所有点都在由方程 \((6-5)\) 所表示的曲线上。

方程 \((6-5)\) 表示一个母线平行于 \(z\) 轴的柱面。由上面的讨论可知，这柱面必定包含曲线 \(C\) 。以曲线 \(C\) 为准线、母线平行于 \(z\) 轴（即垂直于 \(xOy\) 面）的柱面叫做曲线 \(C\) 关于 \(xOy\) 面的 投影柱面 ，投影柱面与 \(xOy\) 面的交线叫做空间曲线 \(C\) 在 \(xOy\) 面上的 投影曲线 ，或简称 投影 。因此，方程 \((6-5)\) 所表示的柱面必定包含投影柱面，而方程

\[\begin{equation*} \begin{cases} H(x, y) = 0, \\ z = 0 \end{cases} \end{equation*} \]

所表示的曲线必定包含空间曲线 \(C\) 在 \(xOy\) 面上的投影。

同理，消去方程组 \((6-1)\) 中的变量 \(x\) 或变量 \(y\) ，再分别和 \(x = 0\) 或 \(y = 0\) 联立，我们就可得到包含曲线 \(C\) 在 \(yOz\) 面或 \(zOx\) 面上的投影的曲线方程

\[\begin{equation*} \begin{cases} R(y, z) = 0, \\ x = 0, \end{cases} \quad 或 \quad \begin{cases} T(x, z) = 0, \\ y = 0. \end{cases} \end{equation*} \]

8.6例4

8.6例5

posted @ 2025-08-19 20:46  暮颜  阅读(44)  评论(0)    收藏  举报