一、数量积

对两个向量做运算 \(\boldsymbol{a}\) 和 \(\boldsymbol{b}\) ，运算结果是一个数，它等于 \(|\boldsymbol{a}|\) ，\(|\boldsymbol{b}|\) 及它们的夹角 \(\theta\) 的余弦的乘积。我们把它叫做向量 \(\boldsymbol{a}\) 和 \(\boldsymbol{b}\) 的数量积，记作 \(\boldsymbol{a} \cdot \boldsymbol{b}\) ，即

由于 \(|\boldsymbol{b}| \cos \theta = |\boldsymbol{b}| \cos{(\widehat{\boldsymbol{a}, \boldsymbol{b}})}\) ，当 \(\boldsymbol{a} \neq \boldsymbol{0}\) 时是向量 \(\boldsymbol{b}\) 在向量 \(\boldsymbol{a}\) 方向上的投影，用 \(\mathrm{Prj}_{\boldsymbol{a}} \boldsymbol{b}\) 来表示这个投影，便有

同理，当 \(\boldsymbol{b} \neq \boldsymbol{0}\) 时有

这就是说，两向量的数量积等于其中一个向量的模和另一个向量在这个向量的方向上的投影的乘积。

由数量积的定义可以推得
（1）\(\boldsymbol{a} \cdot \boldsymbol{a} = |\boldsymbol{a}|^2\) ;
（2）对于两个非零向量 \(\boldsymbol{a}, \boldsymbol{b}\) ，如果 \(\boldsymbol{a} \cdot \boldsymbol{b} = 0\) ，那么 \(\boldsymbol{a} \perp \boldsymbol{b}\) ；反之，如果 \(\boldsymbol{a} \perp \boldsymbol{b}\) ，那么 \(\boldsymbol{a} \cdot \boldsymbol{b} = 0\) .

由于可以认为零向量与任何向量都垂直，因此，向量 \(\boldsymbol{a} \perp \boldsymbol{b}\) 的充分必要条件是 \(\boldsymbol{a} \cdot \boldsymbol{b} = 0\)

数量积符合下列运算规律

（1）交换律 \(\boldsymbol{a} \cdot \boldsymbol{b} = \boldsymbol{b} \cdot \boldsymbol{a}\) .
（2）分配律 \((\boldsymbol{a} + \boldsymbol{b}) \cdot \boldsymbol{c} = \boldsymbol{a} \cdot \boldsymbol{c} + \boldsymbol{b} \cdot \boldsymbol{c}\) .
（3）\((\lambda \boldsymbol{a}) \cdot \boldsymbol{b} = \lambda (\boldsymbol{a} \cdot \boldsymbol{b})\) .

设 \(\boldsymbol{a} = a_x \boldsymbol{i} + a_y \boldsymbol{j} + a_z \boldsymbol{k}, \boldsymbol{b} = b_x \boldsymbol{i} + b_y \boldsymbol{j} + b_z \boldsymbol{k}\) ，则两个向量的数量积的坐标表示式为

因为 \(\boldsymbol{a} \cdot \boldsymbol{b} = |\boldsymbol{a}| |\boldsymbol{b}| \cos \theta\) ，所以当 \(\boldsymbol{a}\) 与 \(\boldsymbol{b}\) 都不是零向量时，有

将数量积的坐标表示式及向量的模的坐标表示式代入上式，就得到两向量夹角余弦的坐标表示式：

二、向量积

设向量 \(\boldsymbol{c}\) 有两个向量 \(\boldsymbol{a}\) 与 \(\boldsymbol{b}\) 按下列方式定出：

\(\boldsymbol{c}\) 的模 \(|\boldsymbol{c}| = |\boldsymbol{a}| |\boldsymbol{b}| \sin \theta\) ，其中 \(\theta\) 为 \(\boldsymbol{a}\) 与 \(\boldsymbol{b}\) 的夹角；\(\boldsymbol{c}\) 垂直于 \(\boldsymbol{a}\) 与 \(\boldsymbol{b}\) 所决定的平面（即 \(\boldsymbol{c}\) 垂直于 \(\boldsymbol{a}\) ，又垂直于 \(\boldsymbol{b}\)），\(\boldsymbol{c}\) 的正向按右手定则从 \(\boldsymbol{a}\) 转向 \(\boldsymbol{b}\) 来确定，向量 \(\boldsymbol{c}\) 叫做向量 \(\boldsymbol{a}\) 与 \(\boldsymbol{b}\) 的向量积，记作 \(\boldsymbol{a} \times \boldsymbol{b}\) ，即

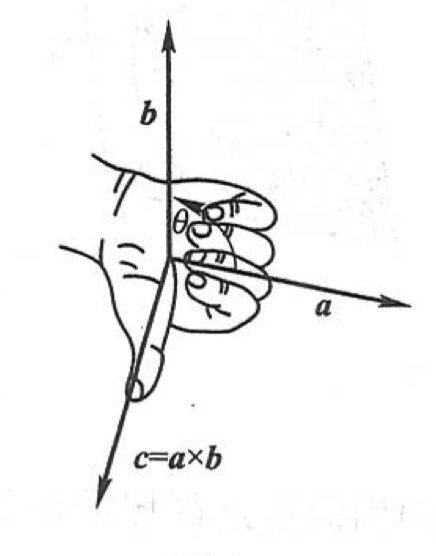
由数量积的定义可以推得

（1）\(\boldsymbol{a} \times \boldsymbol{a} = \boldsymbol{0}\) .
（2）对于两个非零向量 \(\boldsymbol{a}, \boldsymbol{b}\) ，如果 \(\boldsymbol{a} \times \boldsymbol{b} = \boldsymbol{0}\) ，那么 \(\boldsymbol{a} \parallel \boldsymbol{b}\) ；反之，如果 \(\boldsymbol{a} \parallel \boldsymbol{b}\) ，那么 \(\boldsymbol{a} \times \boldsymbol{b} = \boldsymbol{0}\) .
由于可以认为零向量与任何向量都平行，因此，向量 \(\boldsymbol{a} \parallel \boldsymbol{b}\) 的充分必要条件是 \(\boldsymbol{a} \times \boldsymbol{b} = \boldsymbol{0}\) .

向量积符合下列运算规律：

（1）\(\boldsymbol{b} \times \boldsymbol{a} = - \boldsymbol{a} \times \boldsymbol{b}\) .
（2）分配律 \((\boldsymbol{a} + \boldsymbol{b}) \times \boldsymbol{c} = \boldsymbol{a} \times \boldsymbol{c} + \boldsymbol{b} \times \boldsymbol{c}\) .
（3）结合律 \((\lambda \boldsymbol{a}) \times \boldsymbol{b} = \boldsymbol{a} \times (\lambda \boldsymbol{b}) = \lambda (\boldsymbol{a} \times \boldsymbol{b}) \quad (\lambda 为数)\) 。

设 \(\boldsymbol{a} = a_x \boldsymbol{i} + a_y \boldsymbol{j} + a_z \boldsymbol{k}, \boldsymbol{b} = b_x \boldsymbol{i} + b_y \boldsymbol{j} + b_z \boldsymbol{k}\) ，则向量积 \(\boldsymbol{a} \times \boldsymbol{b}\) 为

利用三阶行列式，上式可写成

三、*混合积

设已知三个向量 \(\boldsymbol{a}, \boldsymbol{b}\) 和 \(\boldsymbol{c}\) 。先做两向量 \(\boldsymbol{a}\) 和 \(\boldsymbol{b}\) 的向量积 \(\boldsymbol{a} \times \boldsymbol{b}\) ，把所得到的向量与第三个向量 \(\boldsymbol{c}\) 再作数量积 \((\boldsymbol{a} \times \boldsymbol{b}) \cdot \boldsymbol{c}\) ，这样得到的数叫做三向量\(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\) 的混合积，记作 \([\boldsymbol{a} \ \boldsymbol{b} \ \boldsymbol{c}]\) 。

设 \(\boldsymbol{a} = (a_x, a_y, a_z), \boldsymbol{b} = (b_x, b_y, b_z), \boldsymbol{c} = (c_x, c_y, c_z)\) ，则三向量的混合积的坐标表示式为

向量的混合积的几何意义：
向量的混合积 \([\boldsymbol{a} \ \boldsymbol{b} \ \boldsymbol{c}] = (\boldsymbol{a} \times \boldsymbol{b}) \cdot \boldsymbol{c}\) 是这样一个数，它的绝对值表示以向量 \(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\) 为棱的平行六面体的体积。如果向量 \(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\) 组成右手系（即 \(\boldsymbol{c}\) 的方向按右手规则从 \(\boldsymbol{a}\) 转向 \(\boldsymbol{b}\) 来确定），那么混合积的符号是正的；如果向量 \(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\) 组成左手系（即 \(\boldsymbol{c}\) 的方向按左手规则从 \(\boldsymbol{a}\) 转向 \(\boldsymbol{b}\) 来确定），那么混合积的符号是负的。

由混合积的几何意义可知，若混合积 \([\boldsymbol{a} \ \boldsymbol{b} \ \boldsymbol{c}] \neq 0\) ，则能以 \(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\) 三向量为棱构成平行六面体，从而 \(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\) 三向量不共面；反之，若 \(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\) 三向量不共面，则必能以 \(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\) 为棱构成平行六面体，从而 \([\boldsymbol{a} \ \boldsymbol{b} \ \boldsymbol{c}] \neq 0\) 。于是有下述结论：
三向量 \(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\) 共面的充分必要条件是它们的混合积 \([\boldsymbol{a} \ \boldsymbol{b} \ \boldsymbol{c}] = 0\) ，即