利用导数描绘函数图形的一般步骤如下：
（1）确定函数 \(y = f(x)\) 的定义域及函数所具有的某些特性（如奇偶性、周期性等），并求出函数的一阶导数 \(f^{'}(x)\) 和二阶导数 \(f^{''}(x)\) ；
（2）求出一阶导数 \(f^{'}(x)\) 和二阶导数 \(f^{''}(x)\) 在函数定义域内的全部零点，并求出函数 \(f(x)\) 的间断点及 \(f^{'}(x)\) 和 \(f^{''}(x)\) 不存在的点，用这些点把函数的定义域划分成几个部分区间；
（3）确定这些部分区间内 \(f^{'}(x)\) 和 \(f^{''}(x)\) 的符号，并由此确定函数图形的升降、凹凸和拐点；
（4）确定函数图形的水平、铅直渐近线以及其他变化趋势；
（5）算出 \(f^{'}(x)\) 和 \(f^{''}(x)\) 的零点以及不存在的点所对应的函数值，定出图形上相应的点；为了把图形描绘的更准确些，有时还需补充一些点，然后结合第（3）、（4）步中得到的结果，连接这些点画出函数 \(y = f(x)\) 的图形。

例 描绘函数 \(y = 1 + \cfrac{36x}{(x + 3)^2}\) 的图形。
解：（1）所给函数 \(y = f(x)\) 的定义域为 \((- \infty, -3) \cup (-3, \infty)\) .

（2）\(f^{'}(x)\) 的零点为 \(x = 3\) ; \(f^{''}(x)\) 的零点为 \(x = 6\) ；\(x = -3\) 是函数的间断点。点 \(x = -3\) ，\(x = 3\) ，\(x = 6\) 把定义域划分为四个部分区间：

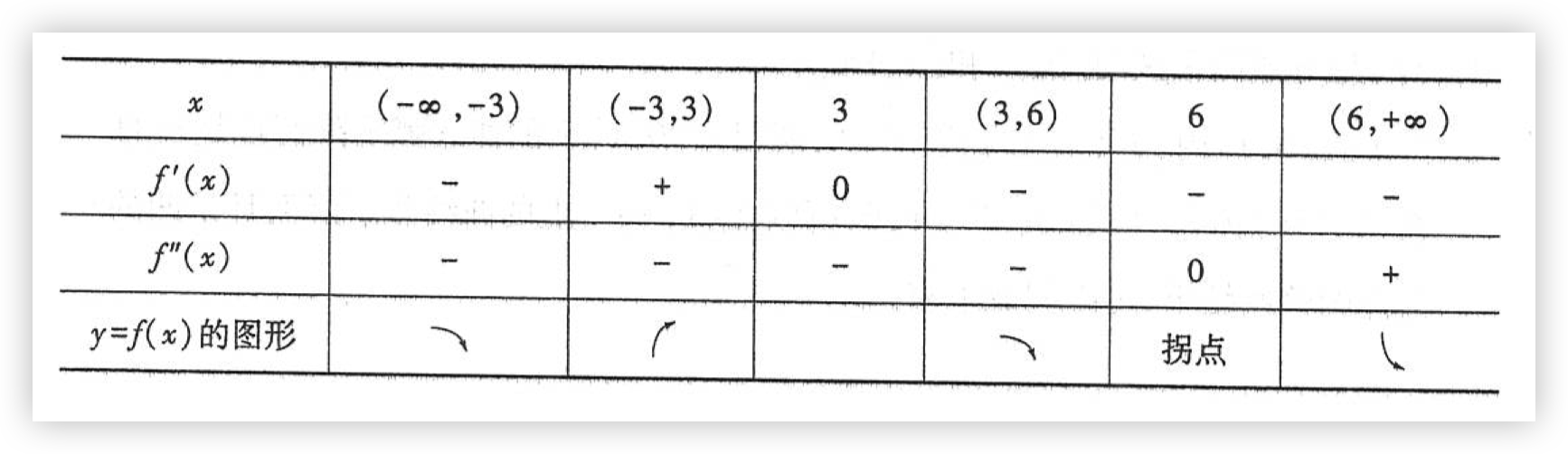
（4）由于 \(\lim \limits_{x \to + \infty} f(x) = 1\) ，\(\lim \limits_{x \to -3} f(x) = - \infty\) ，所以图形有一条水平渐近线 \(y = 1\) 和一条铅直渐近线 \(x = -3\) .
（5）计算出 \(x = 3\) ，\(x = 6\) 处的函数值：

从而得到图形上的两个点

又由于

得图形上的四个点

结合（3）、（4）中得到的结果，画出函数 \(y = 1 + \cfrac{36x}{(x + 3)^2}\) 的图形如下图