莫比乌斯反演 超级详细推导
莫比乌斯反演
今天是世纪性的一天,因为我又又又又来看数论且弄懂了qwq。
前置知识: , (我们需要将式子化为整数分块可以解决的形式)
莫比乌斯函数
->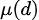
函数构成
- 当
![]() 时,
时,![]()
- 当
![]()
![]() ,且
,且![]() 为互异质数时,
为互异质数时,![]() ;
;
(也就是就是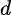 分解质因数后,没有幂次大于2的质因子,此时函数值根据分解的个数决定)
分解质因数后,没有幂次大于2的质因子,此时函数值根据分解的个数决定)
- 只要
![]() 含有任何质因子的幂次大于等于2,则
含有任何质因子的幂次大于等于2,则![]()
![]()
性质
- 对于任意正整数
![]() ,
,![]()
![]()
- 对于任意正整数
![]() ,
,![]()
![]()
![]()
code
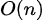 版本,如果超时请去学杜教筛
版本,如果超时请去学杜教筛
云剪贴板 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
注意
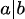 的意思为b除以a为整数(b为a的倍数),即a能整除b
的意思为b除以a为整数(b为a的倍数),即a能整除b
莫比乌斯反演
定理
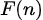 和
和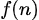 是定义在非负整数集合上的两个函数,它们之间满足关系
是定义在非负整数集合上的两个函数,它们之间满足关系
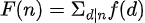
那么就有结论
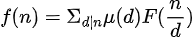
这个定理即为莫比乌斯反演定理.
还有另外一种形式
若
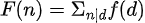
则
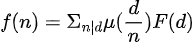
证明
这里只给出第一种形式的证明,第二种形式同理.
由定理可设
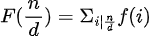
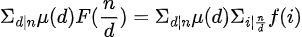
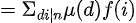 //这一步没看懂的去看交换求和,接下来都为交换求和的知识点
//这一步没看懂的去看交换求和,接下来都为交换求和的知识点
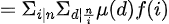
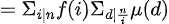
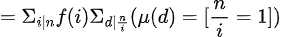
//(莫比乌斯函数性质1)只有在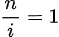 时才有值,其他时候为0;
时才有值,其他时候为0;
//因此
//故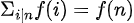
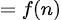
得证.
例题
P2257 YY的GCD - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
观察定理可知,我们在反演前需要设出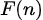 与
与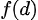
而对于这种有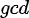 的题目,一般套路为将
的题目,一般套路为将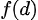 设为
设为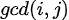
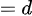 的对数,将
的对数,将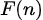 设为
设为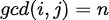 或n的倍数的对数;
或n的倍数的对数;
(对数为满足条件的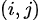 对数)
对数)
即有
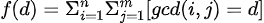
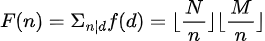
带入反演公式后有
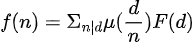
接下来开始计算答案
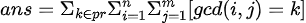
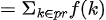 //反演
//反演
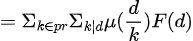
为了将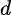 消去,设
消去,设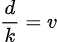
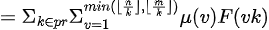
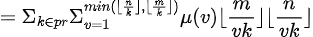
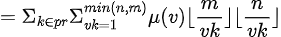
由于我们需要将式子向整除分块,即形如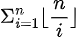 的形式
的形式
所以我们设
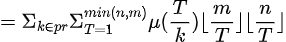
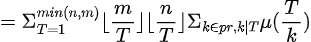
接下来就可以开始运算啦
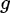 为
为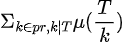 ,即
,即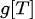
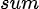 为
为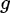 的前缀和,用来计算整除分块.
的前缀和,用来计算整除分块.
code


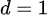 时,
时,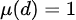
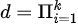
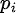 ,且
,且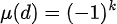 ;
;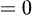
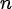 ,
,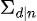
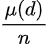
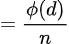

 浙公网安备 33010602011771号
浙公网安备 33010602011771号