FFT变换仿真作业 笔记
本周要完成的作业
记录一下可以用的参考资料
需要实现2种方法,也就是奇偶和虚实的方法对噪声进行fft变换
然后再算加权和不加权的方法
白噪声?
一个DIT也就是奇偶变换的fft,比较好的资料
https://blog.csdn.net/grace_fight/article/details/83515402
DIF,DIT FFT
DIF
http://blog.sina.com.cn/s/blog_65906d030100qicu.html
dit dif
https://wenku.baidu.com/view/28039d6da417866fb84a8e42.html
https://www.cnblogs.com/zhaojihui/p/6684208.html
谱级
https://zhuanlan.zhihu.com/p/102303274
谱级是指定信号在某一频率的谱密度与基准纳密度之比的以10为底的对数乘以10,以分贝计。只适用于对所读频率范围内为连续谱的信号。
谱级:
可以理解为某一带宽下能量的分布:
上式中 为信号的带宽,参考带宽
为1赫兹。
频域上是对应频点下单频信号幅值的N/2倍,而任意单频信号
幅度有效值为
,因此离散信号的谱级为:
所以对FFT后的序列乘以 再取对数即为信号的谱级图谱。
噪声中的加权-什么是加权
http://www.elecfans.com/d/1213145.html
噪音一般用分贝(dB)来表示噪声的大小,信噪比(S/N)来表示噪声对有用信号的影响程度。测量信噪比时通常会标注加权还是不加权。什么是加权和不加权呢?
介绍加权之前,先介绍测量带宽。由于噪声具有频谱扩散特性,其测量只有在说明了测量带宽的前提下才有意义。在噪声测量仪器中使用技术指标要求的带通和加权滤波器,才能准确比较实际噪声测量结果和噪声指标间的差异。
广播和民用音频频应用中最常用的噪声测量带宽是20Hz~20kHz, 也有CCIR468技术规定写的是22Hz~22kHz,都差不多。如果是纯粹在通讯应用中,由于通讯质量的语音要求带宽要窄得多,因此常用的技术指标为300Hz~3.5kHz。
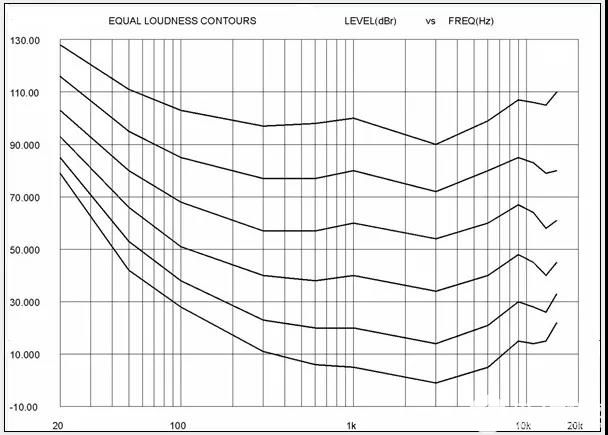
加权:实际上就是加滤波器。加权是为模拟人耳听觉对不同频率的声音有不同灵敏度的特性,在噪声测试仪内设计的一种特殊的滤波器。在测量中使用加权滤波器,可使测量结果与未加权的测量结果相比更能与人耳感知相吻合。人耳的灵敏度是不平坦的,其随频率而变化,同时人耳的频率响应还会随声压级的幅度不同而改变,例如下图展示了纯音的等响度频响曲线。所以音响等应用中,加权噪声是更贴合实际应用的。例如在100K高频有很大的噪音,如果不加权,测试出来指标很差,但是人耳根本无法听到。
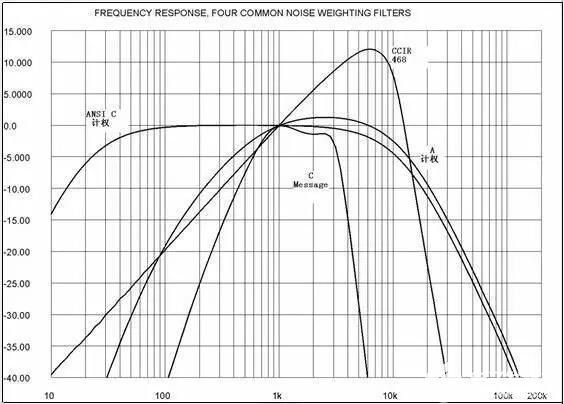
A加权:不同的加权滤波器开发者假定了不同的声压级应用,所以他们使用Fletcher-Munson中的不同曲线。我们最熟悉的就是A加权了。它是目前世界上最广泛应用的指标,主要是因为A加权是模拟人耳对40方纯音的响度,当信号通过时,其低频、中段频(1000Hz以下)有较大的衰减。由于其特性曲线接近于人耳的听感特性,许多与噪声有关的规范都是按A加权作为指标的。
关于白噪声
一、概念
英文名称:white Gaussian noise; WGN
定义:均匀分布于给定频带上的高斯噪声;
所谓高斯白噪声中的高斯是指概率分布是正态函数,而白噪声是指它的二阶矩不相关,一阶矩为常数,是指先后信号在时间上的相关性。这是考察一个信号的两个不同方面的问题。
高斯白噪声:如果一个噪声,它的幅度服从高斯分布,而它的功率谱密度又是均匀分布的,则称它为高斯白噪声。
热噪声和散粒噪声是高斯白噪声。
二、matlab举例
Matlab有两个函数可以产生高斯白噪声,wgn( )和awgn( )。
1. WGN:产生高斯白噪声
y = wgn(m,n,p)
y = wgn(m,n,p) %产生一个m行n列的高斯白噪声的矩阵,p以dBW为单位指定输出噪声的强度。
y = wgn(m,n,p,imp)
y = wgn(m,n,p,imp) %以欧姆(Ohm)为单位指定负载阻抗。
y = wgn(m,n,p,imp,state)
y = wgn(m,n,p,imp,state) %重置RANDN的状态。
在数值变量后还可附加一些标志性参数:
y = wgn(…,POWERTYPE) 指定p的单位。POWERTYPE可以是'dBW', 'dBm'或'linear'。线性强度(linear power)以瓦特(Watt)为单位。
y = wgn(…,OUTPUTTYPE) 指定输出类型。OUTPUTTYPE可以是'real'或'complex'
2. AWGN:在某一信号中加入高斯白噪声
y = awgn(x,SNR)
y = awgn(x,SNR) %在信号x中加入高斯白噪声。信噪比SNR以dB为单位。x的强度假定为0dBW。如果x是 复数,就加入复噪声。
y = awgn(x,SNR,SIGPOWER) 如果SIGPOWER是数值,则其代表以dBW为单位的信号强度;如果SIGPOWER为'measured',则函数将在加入噪声之前测定信号强度。
y = awgn(x,SNR,SIGPOWER,STATE) 重置RANDN的状态。
y = awgn(…,POWERTYPE) 指定SNR和SIGPOWER的单位。POWERTYPE可以是'dB'或'linear'。如果POWERTYPE是'dB',那么SNR以dB为单位,而SIGPOWER以dBW为单位。如果POWERTYPE是'linear',那么SNR作为比值来度量,而SIGPOWER以瓦特为单位
关于FFT
FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
模拟信号经过ADC采样之后变成数字信号,可对此数字信号做FFT变换。N个采样点经过FFT之后就可以得到N个点的FFT结果。为了方便进行FFT运算,通常N取2的整数次幂。
假设采样频率为Fs,信号频率为F,采样点数为N。则FFT之后结果为N点复数,其中每一个点对应着一个频率点,该点复数的模值为原始信号在该频率值下的幅度特性。具体为:假设原始信号在某频率点的幅值为A,则该频点对应的FFT点复数的模值为A的N/2倍。而FFT第一点为原始信号的直流分量,其模值为原始信号模值的N倍。对于相位,FFT复数的相位即为原始信号在该频率点处的相位。
FFT后的N点复数,第一点表示直流分量(0Hz),而最后一点的下一点(实际不存在,假设为第N+1点)表示的频率为采样频率(Fs),这中间被N-1个点平均分为N等份,每点频率依次增加。例如,第k点所表示的频率为:FK=(K-1)Fs/N。所以FFT所能达到的频率分辨率为Fs/N。
FFT结果以N/2(换算为频率即为乃奎斯特频率,Fs/2)对称。因此我们只需要前半部分的结果,即在乃奎斯特频率内的结果。
FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
虽然很多人都知道FFT是什么,可以用来做什么,怎么去做,但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。
现在就根据实际经验来说说FFT结果的具体物理意义。一个模拟信号,经过ADC采样之后,就变成了数字信号。采样定理告诉我们,采样频率要大于信号频率的两倍,这些我就不在此罗嗦了。
采样得到的数字信号,就可以做FFT变换了。N个采样点,经过FFT之后,就可以得到N个点的FFT结果。为了方便进行FFT运算,通常N取2的整数次方。
假设采样频率为Fs,信号频率F,采样点数为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值,就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍。而第一个点就是直流分量,它的模值就是直流分量的N倍。而每个点的相位呢,就是在该频率下的信号的相位。第一个点表示直流分量(即0Hz),而最后一个点N的再下一个点(实际上这个点是不存在的,这里是假设的第N+1个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率Fs,这中间被N-1个点平均分成N等份,每个点的频率依次增加。例如某点n所表示的频率为:Fn=(n-1)*Fs/N。由上面的公式可以看出,Fn所能分辨到频率为为Fs/N,如果采样频率Fs为1024Hz,采样点数为1024点,则可以分辨到1Hz。1024Hz的采样率采样1024点,刚好是1秒,也就是说,采样1秒时间的信号并做FFT,则结果可以分析到1Hz,如果采样2秒时间的信号并做FFT,则结果可以分析到0.5Hz。如果要提高频率分辨力,则必须增加采样点数,也即采样时间。频率分辨率和采样时间是倒数关系。
假设FFT之后某点n用复数a+bi表示,那么这个复数的模就是An=根号a*a+b*b,相位就是Pn=atan2(b,a)。根据以上的结果,就可以计算出n点(n≠1,且n<=N/2)对应的信号的表达式为:An/(N/2)*cos(2*pi*Fn*t+Pn),即2*An/N*cos(2*pi*Fn*t+Pn)。对于n=1点的信号,是直流分量,幅度即为A1/N。
由于FFT结果的对称性,通常我们只使用前半部分的结果,即小于采样频率一半的结果。
下面以一个实际的信号来做说明。
假设我们有一个信号,它含有2V的直流分量,频率为50Hz、相位为-30度、幅度为3V的交流信号,以及一个频率为75Hz、相位为90度、幅度为1.5V的交流信号。用数学表达式就是如下:
S=2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180)
式中cos参数为弧度,所以-30度和90度要分别换算成弧度。我们以256Hz的采样率对这个信号进行采样,总共采样256点。按照我们上面的分析,Fn=(n-1)*Fs/N,我们可以知道,每两个点之间的间距就是1Hz,第n个点的频率就是n-1。我们的信号有3个频率:0Hz、50Hz、75Hz,应该分别在第1个点、第51个点、第76个点上出现峰值,其它各点应该接近0。实际情况如何呢?我们来看看FFT的结果的模值如图所示。
从图中我们可以看到,在第1点、第51点、和第76点附近有比较大的值。我们分别将这三个点附近的数据拿上来细看:
1点: 512+0i
2点: -2.6195E-14 - 1.4162E-13i
3点: -2.8586E-14 - 1.1898E-13i
50点:-6.2076E-13 - 2.1713E-12i
51点:332.55 - 192i
52点:-1.6707E-12 - 1.5241E-12i
75点:-2.2199E-13 -1.0076E-12i
76点:3.4315E-12 + 192i
77点:-3.0263E-14 +7.5609E-13i
很明显,1点、51点、76点的值都比较大,它附近的点值都很小,可以认为是0,即在那些频率点上的信号幅度为0。接着,我们来计算各点的幅度值。分别计算这三个点的模值,结果如下:
1点: 512
51点:384
76点:192
按照公式,可以计算出直流分量为:512/N=512/256=2;50Hz信号的幅度为:384/(N/2)=384/(256/2)=3;75Hz信号的幅度为192/(N/2)=192/(256/2)=1.5。可见,从频谱分析出来的幅度是正确的。
然后再来计算相位信息。直流信号没有相位可言,不用管它。先计算50Hz信号的相位,atan2(-192, 332.55)=-0.5236,结果是弧度,换算为角度就是180*(-0.5236)/pi=-30.0001。再计算75Hz信号的相位,atan2(192, 3.4315E-12)=1.5708弧度,换算成角度就是180*1.5708/pi=90.0002。可见,相位也是对的。根据FFT结果以及上面的分析计算,我们就可以写出信号的表达式了,它就是我们开始提供的信号。
总结:假设采样频率为Fs,采样点数为N,做FFT之后,某一点n(n从1开始)表示的频率为:Fn=(n-1)*Fs/N;该点的模值除以N/2就是对应该频率下的信号的幅度(对于直流信号是除以N);该点的相位即是对应该频率下的信号的相位。相位的计算可用函数atan2(b,a)计算。atan2(b,a)是求坐标为(a,b)点的角度值,范围从-pi到pi。要精确到xHz,则需要采样长度为1/x秒的信号,并做FFT。要提高频率分辨率,就需要增加采样点数,这在一些实际的应用中是不现实的,需要在较短的时间内完成分析。解决这个问题的方法有频率细分法,比较简单的方法是采样比较短时间的信号,然后在后面补充一定数量的0,使其长度达到需要的点数,再做FFT,这在一定程度上能够提高频率分辨力。具体的频率细分法可参考相关文献。
[附录:本测试数据使用的matlab程序]
close all; %先关闭所有图片
Adc=2; %直流分量幅度
A1=3; %频率F1信号的幅度
A2=1.5; %频率F2信号的幅度
F1=50; %信号1频率(Hz)
F2=75; %信号2频率(Hz)
Fs=256; %采样频率(Hz)
P1=-30; %信号1相位(度)
P2=90; %信号相位(度)
N=256; %采样点数
t=[0:1/Fs:N/Fs]; %采样时刻
%信号
S=Adc+A1*cos(2*pi*F1*t+pi*P1/180)+A2*cos(2*pi*F2*t+pi*P2/180);
plot(S);%显示原始信号
title('原始信号');
figure;
Y = fft(S,N); %做FFT变换
Ayy = (abs(Y)); %取模
plot(Ayy(1:N)); %显示原始的FFT模值结果
title('FFT 模值');
figure;
Ayy=Ayy/(N/2); %换算成实际的幅度
Ayy(1)=Ayy(1)/2;
F=([1:N]-1)*Fs/N; %换算成实际的频率值
plot(F(1:N/2),Ayy(1:N/2)); %显示换算后的FFT模值结果
title('幅度-频率曲线图');
figure;
Pyy=[1:N/2];
for i="1:N/2"
Pyy(i)=phase(Y(i)); %计算相位
Pyy(i)=Pyy(i)*180/pi; %换算为角度
end;
plot(F(1:N/2),Pyy(1:N/2)); %显示相位图
title('相位-频率曲线图')
窗函数
https://blog.csdn.net/wordwarwordwar/article/details/68951294
%% 窗函数测试
function main
clc
close all
Ts = 0.001;
Fs = 1/Ts;
%% 原始信号
t = 0:Ts:pi/2;
yt = sin(2*pi*5*t) + sin(2*pi*10*t) + sin(2*pi*15*t);
[Yf, f] = Spectrum_Calc(yt, Fs);
figure
subplot(211)
plot(t, yt)
xlabel('t')
ylabel('y')
title('原始信号')
subplot(212)
plot(f, Yf)
xlabel('f')
ylabel('|Yf|')
xlim([0 100])
ylim([0 1])
title('原始信号频谱')
%% 加窗信号
win = hann(length(t));
yt1 = yt.*win';
[Yf1, f1] = Spectrum_Calc(yt1, Fs);
figure
subplot(211)
plot(t, yt1)
xlabel('t')
ylabel('y')
title('加窗信号')
subplot(212)
plot(f1, 2*Yf1) % 2表示能量系数
xlabel('f')
ylabel('|Yf|')
xlim([0 100])
ylim([0 1])
title('加窗信号频谱')
end
%% 求取频谱
function [Yf, f] = Spectrum_Calc(yt, Fs)
L = length(yt);
NFFT = 2^nextpow2(L);
Yf = fft(yt,NFFT)/L;
Yf = 2*abs(Yf(1:NFFT/2+1));
f = Fs/2*linspace(0,1,NFFT/2+1);
end
窗函数是频谱分析中一个重要的部分,窗函数修正了由于信号的非周期性并减小了频谱中由于泄露而带来的测量不准确性。
快速傅里叶变换假定了时间信号是周期无限的。但在分析时,我们往往只截取其中的一部分,因此需要加窗以减小泄露。窗函数可以加在时域,也可以加在频域上,但在时域上加窗更为普遍。截断效应带来了泄漏,窗函数是为了减小这个截断效应,其设计成一组加权系数。例如,一个窗函数可以定义为:
w(t)=g(t) -T/2<t<T/2
w(t)=0 其他
g(t)是窗函数,T是窗函数的时间.
待分析的数据x(t)则表示为:
x(t)=w(t)*x(t)'
x(t)'表示原始信号,x(t)表示待分析信号。
加窗在时域上表现的是点乘,因此在频域上则表现为卷积。卷积可以被看成是一个平滑的过程。这个平滑过程可以被看出是由一组具有特定函数形状的滤波器,因此,原始信号中在某一频率点上的能量会结合滤波器的形状表现出来,从而减小泄漏。基于这个原理,人们通常在时域上直接加窗。
大多数的信号分析仪一般使用矩形窗(rectangular),汉宁(hann),flattop和其他的一些窗函数。
矩形窗函数:
w(k)=1
汉宁窗:
w(k)=0.5*(1-cos(2*pi*k/(N-1))) 0<=k<=N-1
由于加窗计算中衰减了原始信号的部分能量,因此对于最后的结果还需要加上修正系数。在线性谱分析中,一般使用幅度系数(amplitude correction),在功率谱中,一般使用能量系数(energycorrection)。(这段不清楚在实际中如何用)
matlab中提供了很多窗函数,如下
还提供了显示窗函数的GUI工具,如wvtool可以显示用来显示窗的形状和频域图形,wintool可以打开窗设计和分析工具,如运行
wvtool(hamming(64),hann(64),gausswin(64))
可以对比汉明窗、汉宁窗和高斯窗
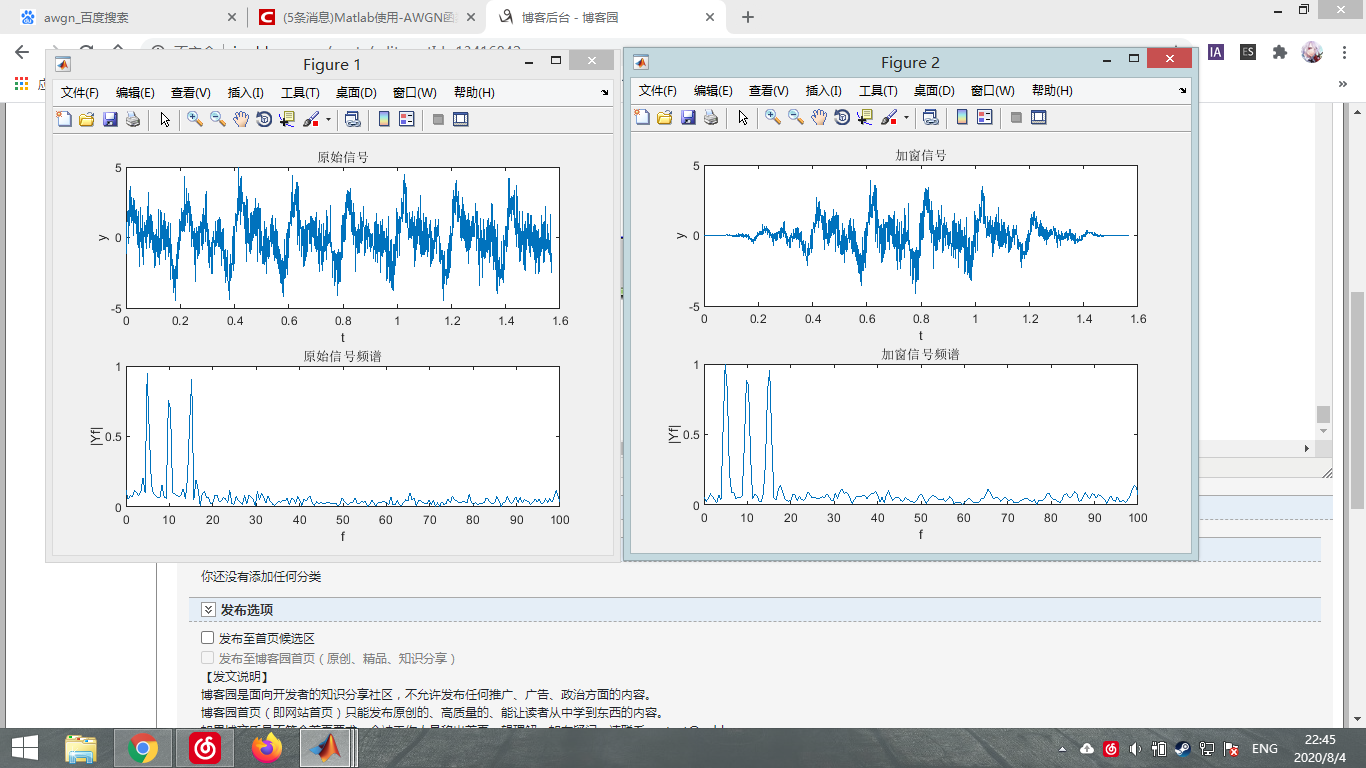
简单测试一下加窗的效果如下
可以看到加窗后,频谱泄露确实减少了,但同时信号能量也减小了,这也许就是所说的要使用能量系数吧,如下,这样一来,对比就更明显了,加窗可以有效的减少频谱泄露。
魔改后的
需要加高斯白噪声







 浙公网安备 33010602011771号
浙公网安备 33010602011771号