计算物理入门

目录

• 矩阵
• 绘图
• 拟合、插值
• 分形
• ODE、PDE
• 其他

对于笔者来讲，一门编程语言最好的入门方式莫过于首先操作实例引起兴趣，在运行过程中了解编程语言的大概知识后再系统地学习。因此笔者在此给出一些计算物理入门代码供读者调试。

阅读本文需要有一定的其他编程语言基础。

矩阵

首先我们对MATLAB最擅长的矩阵进行处理，我们将生成一个矩阵并对计算其标准差。

%% 计算矩阵前4列的标准差
clc;clear all;close all
matr = magic(5); 
std(matr(1:4,:),0,1) 

下面是加入注释的矩阵操作指南

%% 计算矩阵前4列的标准差--注释版
clc;clear all;close all		% 本例中MATLAB程序运行前都可加入此行代码以清理之前程序运行时所保存的数据。
matr = magic(5);    % matr=[16 2 3 13; 5 11 10 8; 9 7 6 12; 4 14 15 1]  空格' '和逗号','表示矩阵行内元素间隔，分号';'表示矩阵换行
matr(4)     % output:4  可以发现MATLAB与Python不同，matrix(n)给出的是第n个元素
matr(4,1)   % output:4  同样MATLAB支持通过(行号,列号)的方法提取元素
% 而且可以发现MATLAB矩阵中元素编号为从左上起先按列进行编号，且第一个元素编号为1 (部分语言初始编号为0)
% 那么如何提取矩阵中特定行或列的矩阵呢？方法如下
matr(1,;)   % output: ans=[16 2 3 13]
matr(:,1)   % output: ans=[16; 5; 9; 4]
matr(3:end,:)   % output: ans=[9 7 6 12; 4 14 15 1]，end表示最后一个元素
% list=start:step:end
% 可以创造一个包含始末元素的列表，但如果(end-start)/step不是整数则也不会包含末尾元素，例如 B=0:1.5:5
% 由此可见MATLAB中矩阵通过由逗号分割的两个元素控制，第一个元素选择行，第二个元素选择列，end表示最后一个元素
% 同时MATLAB不支持负号索引，因此matrix(-1,:)或list(-1)都是不被允许的。
% 接下来我们按照例题要求进行处理，首先取前4列 matr(1:4,:)
% 使用std(matrix,0,1)对矩阵列求标准差
std(matr(1:4,:),0,1)    %output: ans=[5.4467 5.1962 5.1962 5.4467]

矩阵及其他数据类型是MATLAB中最基础的知识，点击传送门可阅读详解文章：MATLALB基础知识

绘图

光计算不做图可不行，数据往往需要通过可视化来更直观的显示，MATLAB作图功能也是非常强大的，我们通过几个例子来体会一下

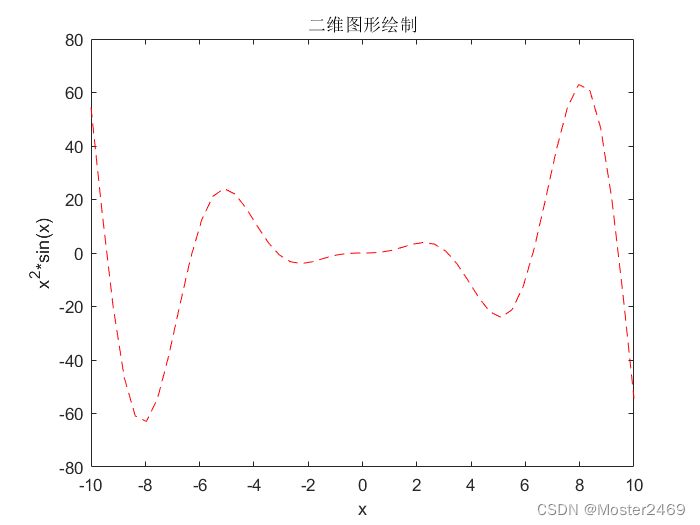
%% 平面图--绘制sin函数图像
clc;clear all;close all
x = linspace(-10,10,50);
y = x.^2.*sin(x);
plot(x,y,'r--')
xlabel('x')
ylabel('x^2*sin(x)')
title('二维图形绘制')


% 使用linspace可以产生向量，linspace(a,b,c)作用相当于 a:(b-a)/(c-1):b，两者会产生一个以a为起点，b为终点，一共c个间距为(b-a)/c的元素。
% 例如 a=linspace(-5,5,11)与b=-5:1:5有一样的效果，二者都会产生包含从-5到5的11个整数的列表。

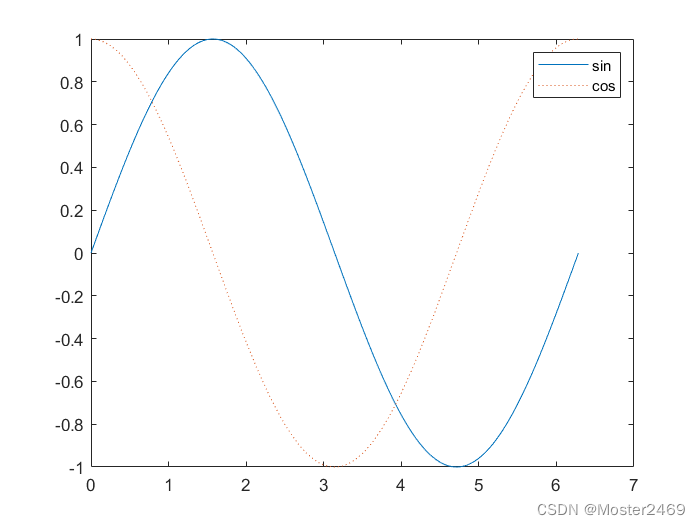
%% 在一个窗口同时绘制多个图像
clc;clear all;close all
x = 0:pi/100:2*pi;
y = sin(x);
plot(x,y)
hold on		% hold on是同时绘制图像的关键函数
y2 = cos(x);
plot(x,y2,':')
legend('sin','cos')
hold off

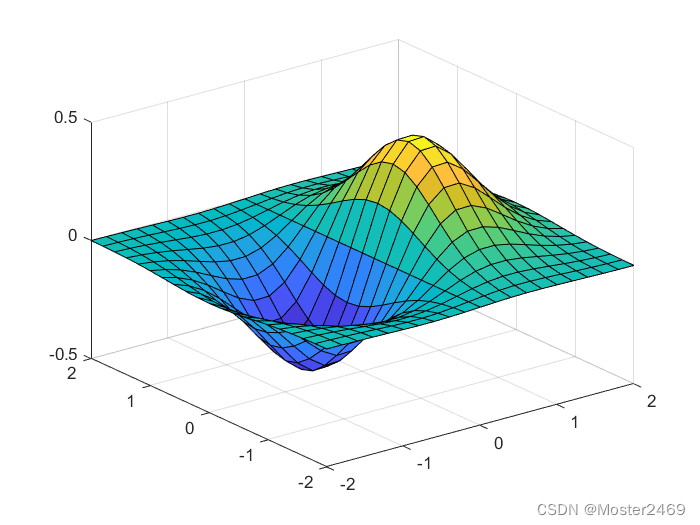
%% 三维绘图
clc;clear all;close all
[X,Y] = meshgrid(-2:.2:2);                                
Z = X .* exp(-X.^2 - Y.^2);
surf(X,Y,Z)

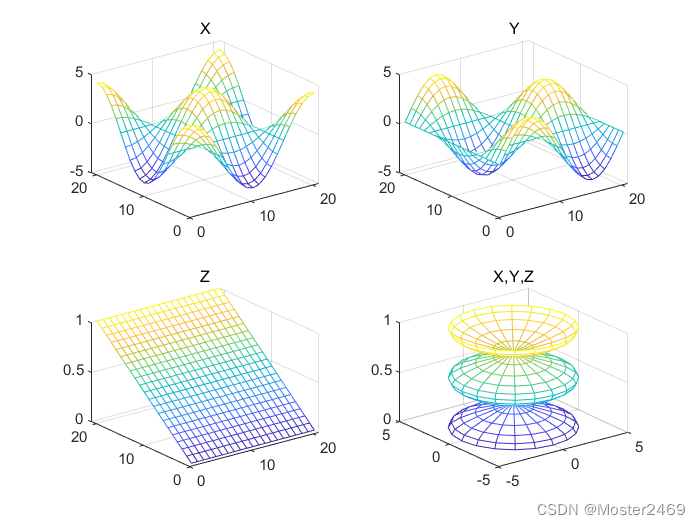
%% 子绘图功能--一张图表内绘制多个子表
t = 0:pi/10:2*pi;
[X,Y,Z] = cylinder(4*cos(t));
subplot(2,2,1); mesh(X); title('X');		% subplot函数前两个元素设置表中每行、每列子表个数，第三个元素确定活动状态的子表位置，注意子表按行进行编号，例如a>2时，subplot(a,b,2)表示第一行第二列的子表。
subplot(2,2,2); mesh(Y); title('Y');
subplot(2,2,3); mesh(Z); title('Z');
subplot(2,2,4); mesh(X,Y,Z); title('X,Y,Z');

MATLAB绘图相关知识及绘图代码传送门：MATLAB绘图

拟合、插值

拟合
拟合在物理中也是十分重要的知识，它可以帮助我们发现物理学中隐藏的规律。

%% 拟合
clc; clear all; close all
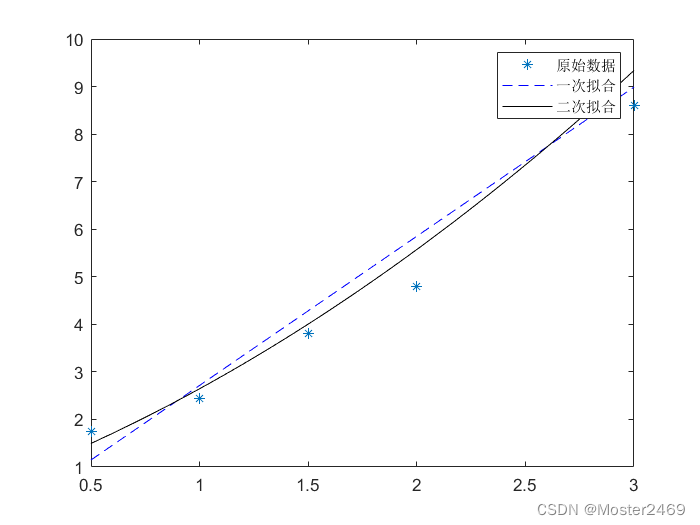
x=[0.5 1.0 1.5 2.0 2.5 3.0];
y=[1.75 2.45 3.81 4.80 9.00 8.60];
a1=polyfit(x,y,1);  % 一次拟合
a2=polyfit(x,y,2);  % 二次拟合
x1=[0.5: 0.05: 3.0];
y1=a1(2)+a1(1)*x1;  % 一次多项式
y2=a2(3)+a2(2)*x1+a2(1).*x1.*x1;    % 二次多项式
plot(x,y,'*')
hold on
plot(x1,y1,'b--', x1,y2,'k');
legend('原始数据', '一次拟合', '二次拟合')
p1=polyval(a1,x)    % 多项式
p2=polyval(a2,x)    % 多项式

插值

clc; clear all; close all
hold off
xx=1:1:17;
yx=[3.5 4 4.3 4.6 5 5.3 5.3 5 4.6 4 3.9 3.3 2.8 2.5 2.2 2.0 1.8];
xxi=1:0.3:17;  % 插值xxi
f0=interp1(xx,yx,xxi);   % 插值
f1=interp1(xx,yx,xxi,'linear');  % 线性插值
f2=interp1(xx,yx,xxi,'cubic');   % 立方插值
f3=interp1(xx,yx,xxi,'spline');  % 样条插值
f4=interp1(xx,yx,xxi,'nearest'); % 最近邻插值
plot(xx,yx,'r--','linewidth',2)
hold on
% plot(xxi,f0,'r.-','linewidth',2)
plot(xxi,f1,'b--','linewidth',2)
plot(xxi,f2,'ro--','linewidth',2)
plot(xxi,f3,'k--','linewidth',2)
plot(xxi,f4,'b','linewidth',2)
legend('原始数据','线性插值','立方插值','样条插值','最近区域插值')    % 标记
grid on

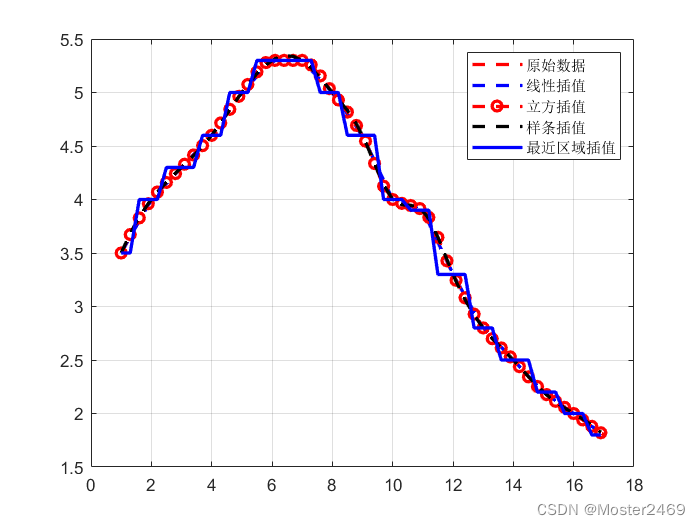
因为插值函数过多，图稍显混乱，可以对代码中不需要的插值函数注释。

学习传送门：MATLAB数据处理 / 插值与拟合

分形

分形树

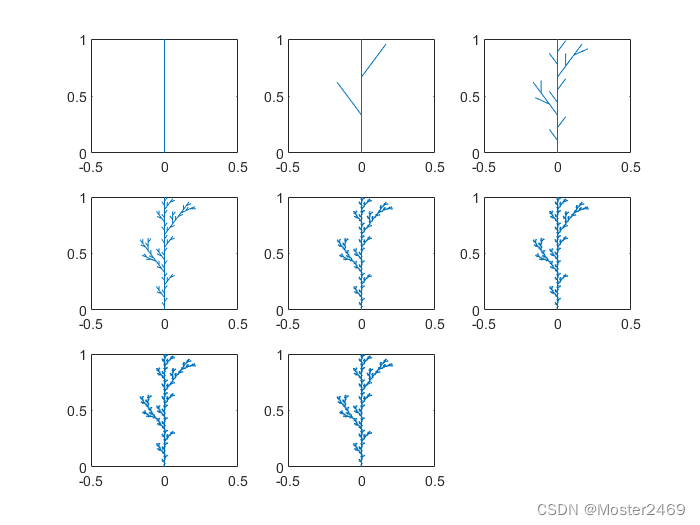
%% 分形树
clc;clear all;close all
u=[0,i];
subplot(3,3,1);
plot(u)
axis([-0.5,0.5,0,1])
for k=2:8
    m=u/3;      %将图形缩小到1/3
    uu=[m,...   %放置缩小后的图形m
        i/3+m*(sqrt(3)*0.5+0.5i),... %将m在虚轴上向上移动1/3后向左旋转
        m+i/3,...       %将m在虚轴上向上移动1/3
        2i/3+m*(sqrt(3)*0.5-0.5i),...   %将m在虚轴上向上移动2/3后向右旋转
        m+2i/3];    %将m在虚轴上移动2/3
    subplot(3,3,k);
    plot(uu)
    axis([-0.5,0.5,0,1])
    u=uu;
end

colormap winter

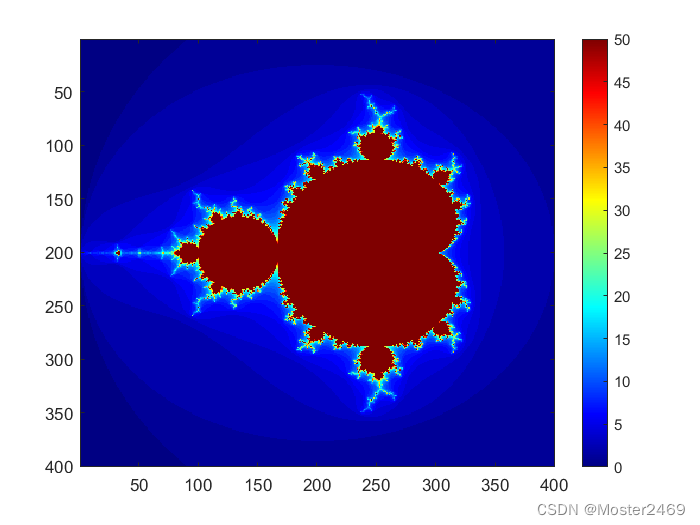
Mandelbrot集

x=linspace(-2.0,1.0,400);   %x的范围与取点数目
y=linspace(-1.5,1.5,400);   %y的范围与取点数目
[Re, Im]=meshgrid(x,y);     
C=Re+i*Im;      %定义常数矩阵C值
B=0;    %矩阵B记录达到逃离时的迭代次数
Z=0;    %Z的初值固定为0
for i=1:50
    Z=Z.*Z+C;  
    B=B+(abs(Z)<=2);
end
imagesc(B);
colormap(jet)
colorbar

ODE、PDE

MATLAB解方程基础知识：MATLAB解方程

常微分方程
例如常微分方程$\ddot{x}=-x$，初始条件若为 $\dot{x}{|}_{t=0}=0,x{|}_{t=0}=2$。

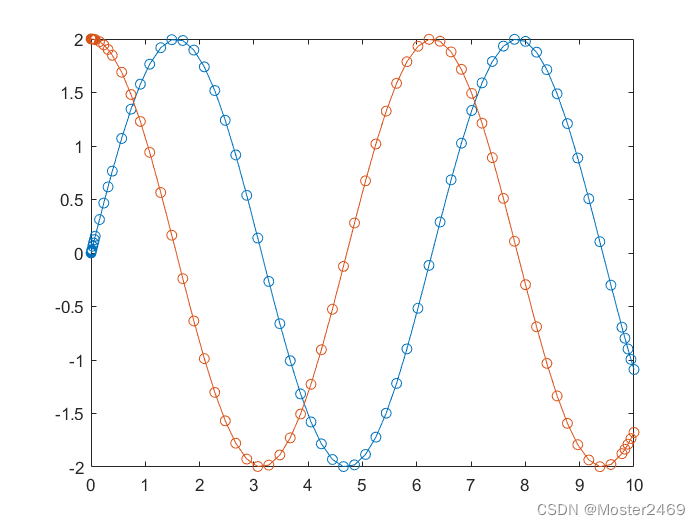
clc;clear;close all
F=@(t,y)[y(2); -y(1)]
ode45(F,[0,10],[0,2])

求解偏微分方程
以有限长细杆的热传导方程为例，定解问题为 $\{\begin{array}{l}{u}_t=a^2{u}_{xx}\\ u(0,t)=0,u(l,t)=0\\ u(x,t=0)=\phi (x)\end{array}$，为了进行数值计算，需给出具体值：$l=20,t=25,a^2=10$且$\phi (x)=\{\begin{array}{l}1(10\le x\le 11)\\ 0(x<10,x>11)\end{array}$。

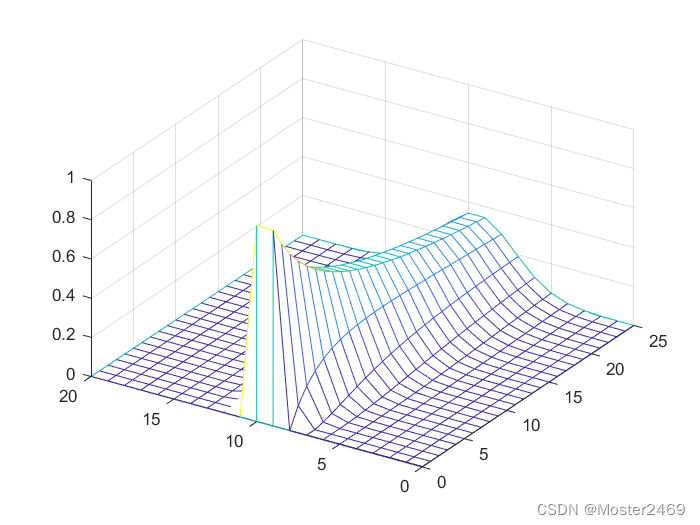
x=0:20; a2=10;  r=a2*0.01;
u=zeros(21,25); % 预设矩阵以存放求得的解
u(10:11,1)=1;   % 初始条件
for j=1:25
    u(2:20,j+1) = (1-2*r)*u(2:20,j) + r*(u(1:19,j)+u(3:21,j));
    plot(x,u(:,j)); axis([0 21 0 1]);   pause(0.1)
end
meshz(u)

其他

%% 其他
% 所有编程语言中最经典的一个，输出Hello world!
disp('Hello world!')		% output:Hello world!