归并排序(Merge Sort)

归并排序

归并排序(Merge Sort) 是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

算法描述

1. 把长度为n的输入序列分成两个长度为n/2的子序列；
2. 对这两个子序列分别采用归并排序；
3. 将两个排序好的子序列合并成一个最终的排序序列。

算法分析

时间复杂度（平均）	时间复杂度（最坏）	时间复杂度（最好）	空间复杂度	稳定性
\(O(n\log_2 n)\)	\(O(n\log_2 n)\)	\(O(n\log_2 n)\)	\(O(n)\)	稳定

例子

归并

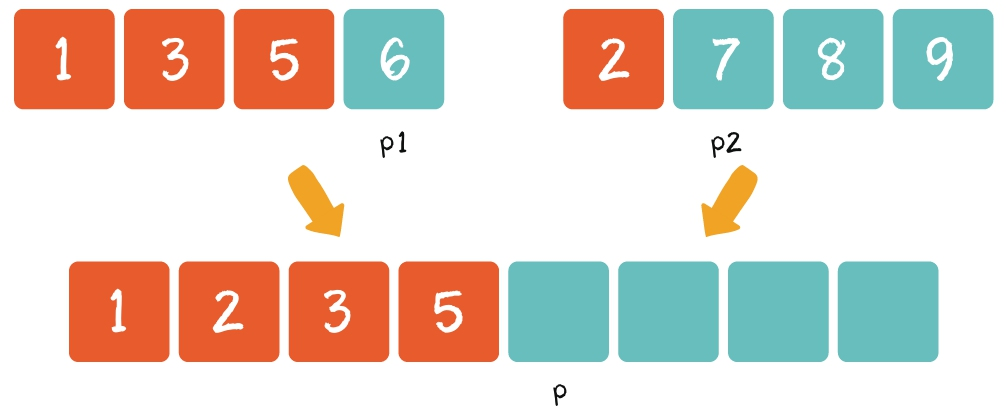
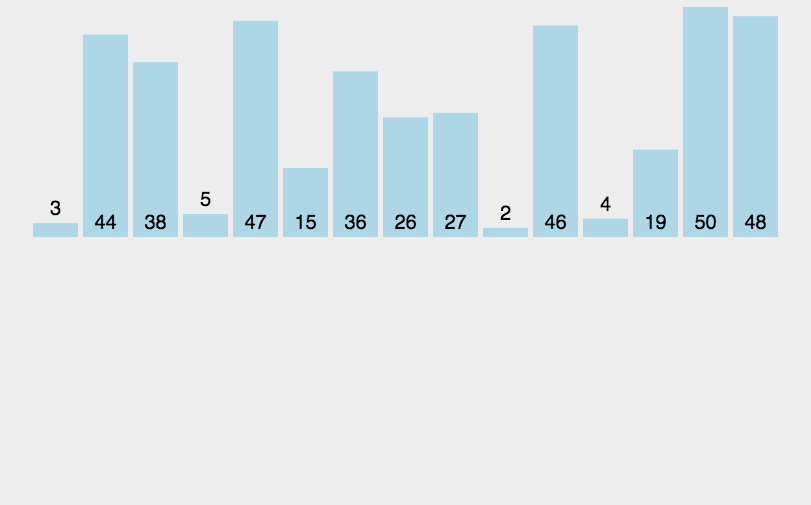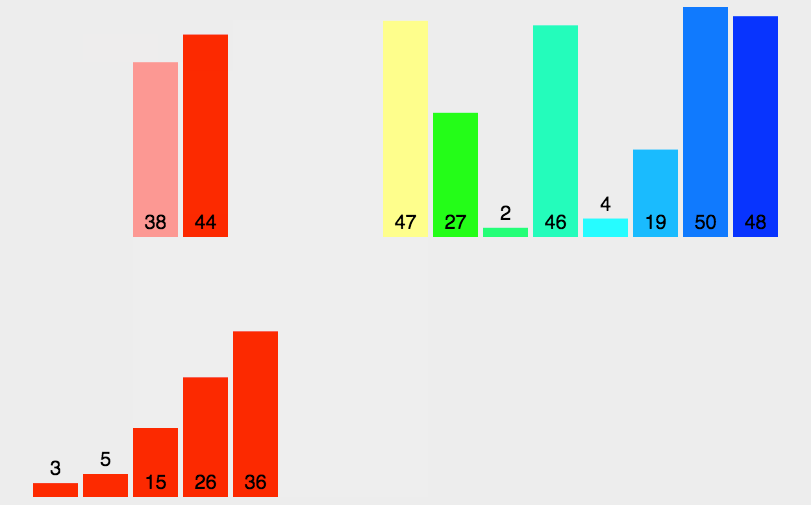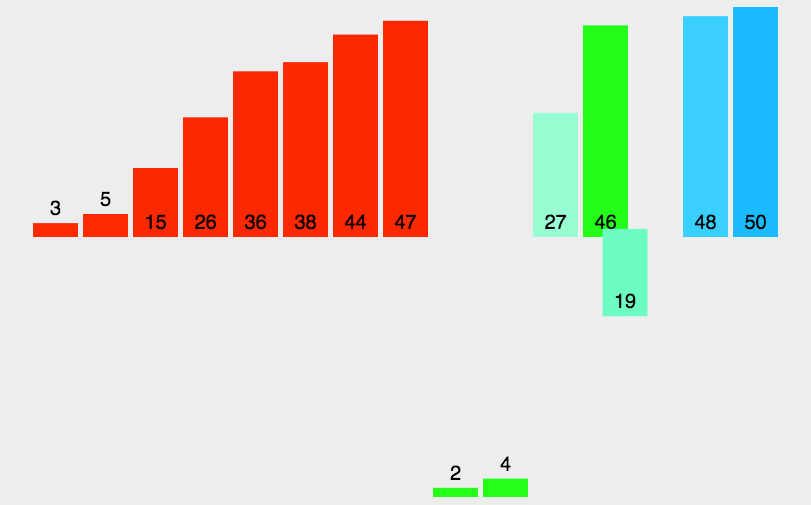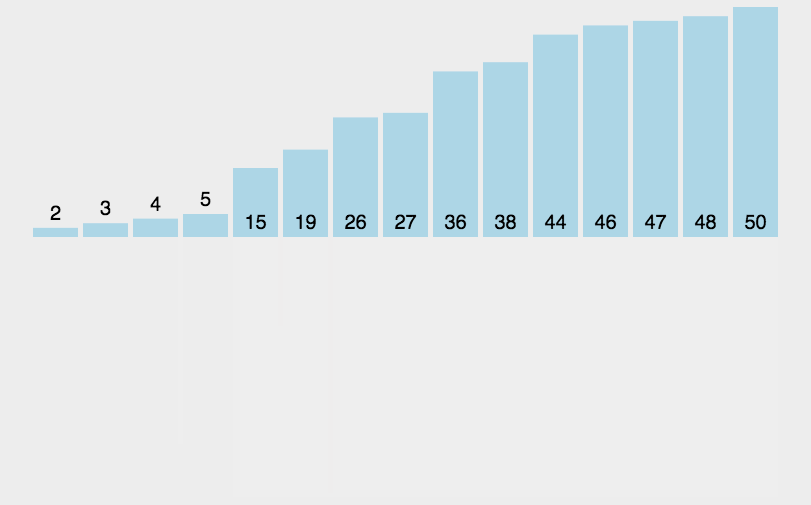
第1步：创建一个额外的大集合，用于存储归并结果，长度是两个小集合之和。（p1，p2，p是三个辅助指针，用于记录当前操作的位置。）

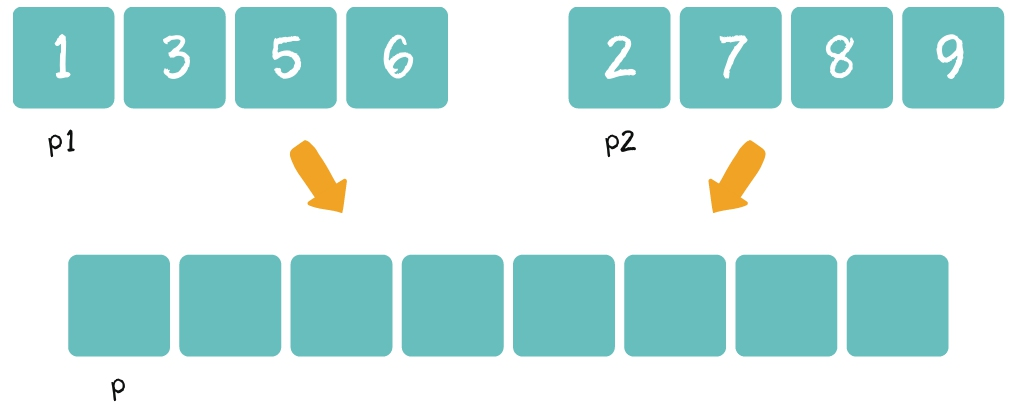
第2步：从左到右逐一比较两个小集合中的元素，把较小的元素优先放入大集合。

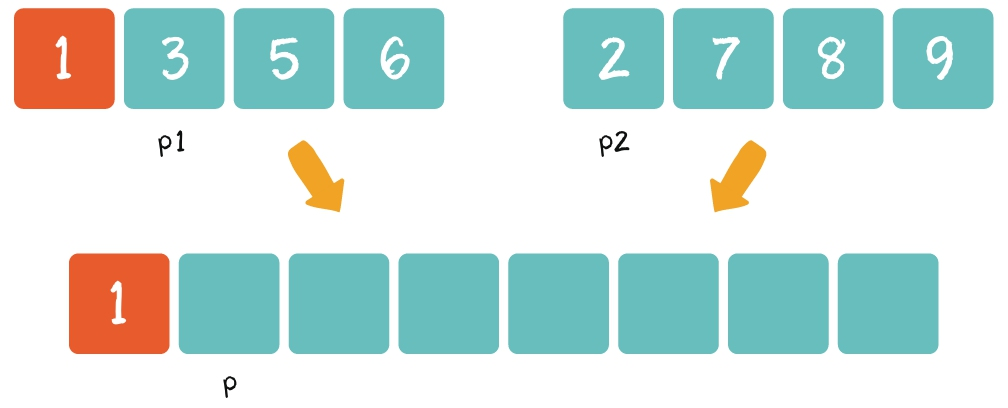
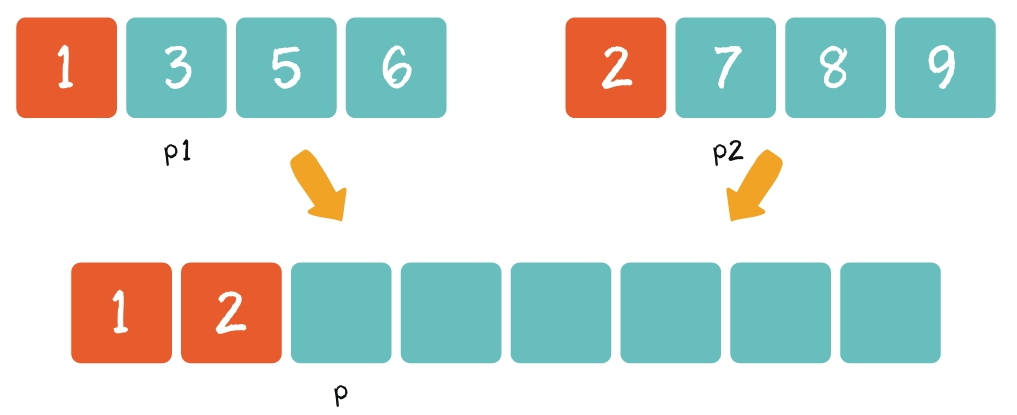
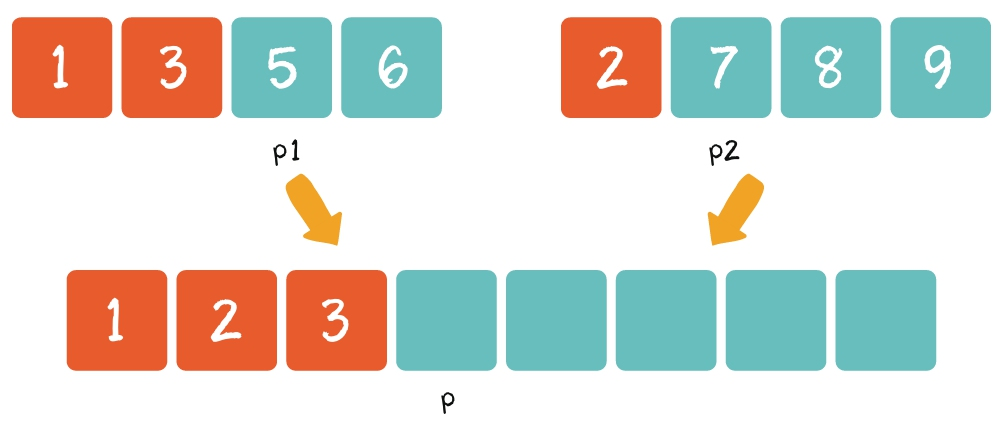
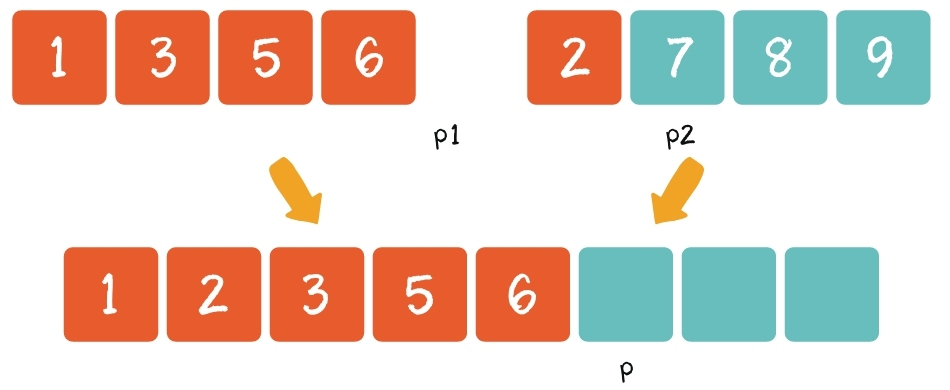
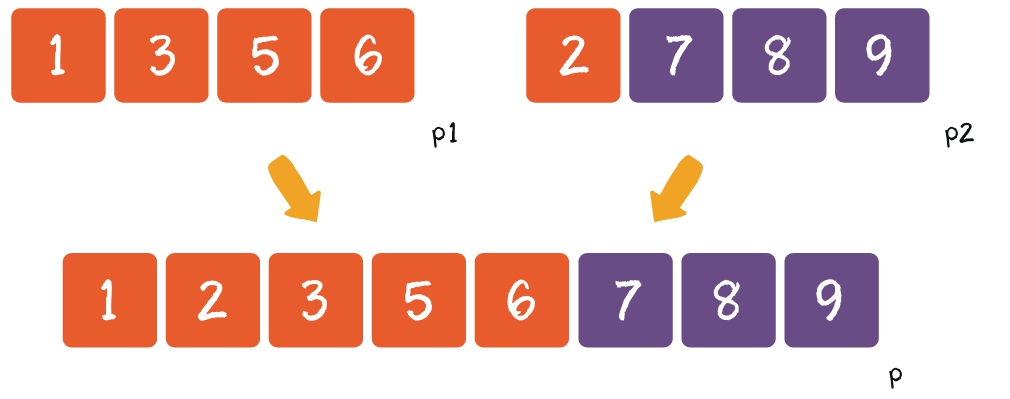
第3步：从另一个还有剩余元素的集合中，把剩余元素按顺序复制到大集合尾部。

代码

Java

public static void mergeSort(int[] array, int start, int end) {
	if (start < end) {
		//折半成两个小集合，分别进行递归
		int mid = (start + end) / 2;
		mergeSort(array, start, mid);
		mergeSort(array, mid + 1, end);
		//把两个有序小集合，归并成一个大集合
		merge(array, start, mid, end);
	}
}

private static void merge(int[] array, int start, int mid, int end) {
	//开辟额外大集合，设置指针
	int[] tempArray = new int[end - start + 1];
	int p1 = start;
	int p2 = mid + 1;
	int p = 0;
	//比较两个小集合的元素，依次放入大集合
	while ((p1 <= mid) && (p2 <= end)) {
		if (array[p1] <= array[p2]) {
			tempArray[p++] = array[p1++];
		}
		else {
			tempArray[p++] = array[p2++];
		}
	}
	//左侧小集合还有剩余，依次放入大集合尾部
	while (p1 <= mid) {
		tempArray[p++] = array[p1++];
	}
	//右侧小集合还有剩余，依次放入大集合尾部
	while (p2 <= end) {
		tempArray[p++] = array[p2++];
	}
	//把大集合的元素复制回原数组
	for (int i = 0; i < tempArray.length; i++) {
		array[i + start] = tempArray[i];
	}
}

python

def mergeSort(arr):
    import math
    if(len(arr)<2):
        return arr
    middle = math.floor(len(arr)/2)
    left, right = arr[0:middle], arr[middle:]
    return merge(mergeSort(left), mergeSort(right))

def merge(left,right):
    result = []
    while left and right:
        if left[0] <= right[0]:
            result.append(left.pop(0));
        else:
            result.append(right.pop(0));
    while left:
        result.append(left.pop(0));
    while right:
        result.append(right.pop(0));
    return result