快速排序(Quick Sort)

快速排序

快速排序(Quick Sort) 的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

算法描述

快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：

1. 从数列中挑出一个元素，称为 “基准”（pivot）；
2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

算法分析

时间复杂度（平均）	时间复杂度（最坏）	时间复杂度（最好）	空间复杂度	稳定性
\(O(n\log_2 n)\)	\(O(n^2)\)	\(O(n\log_2 n)\)	\(O(n\log_2 n)\)	不稳定

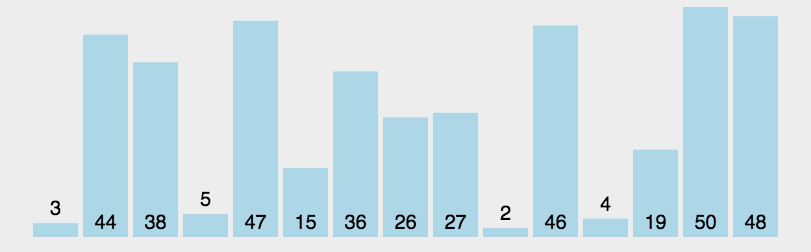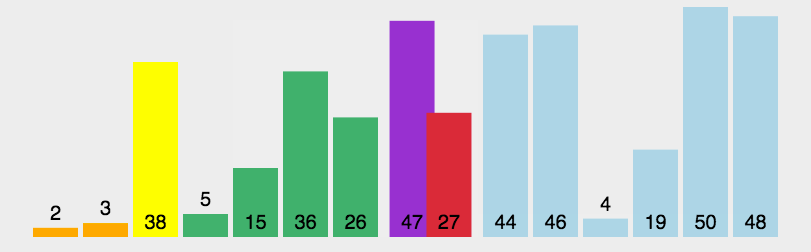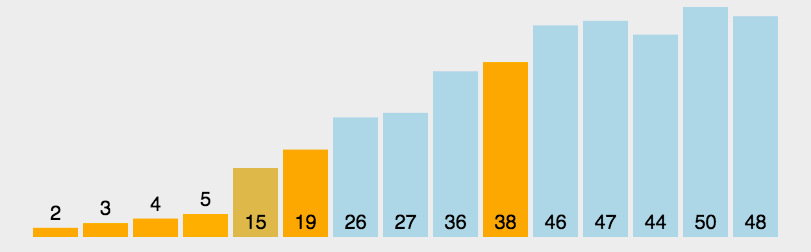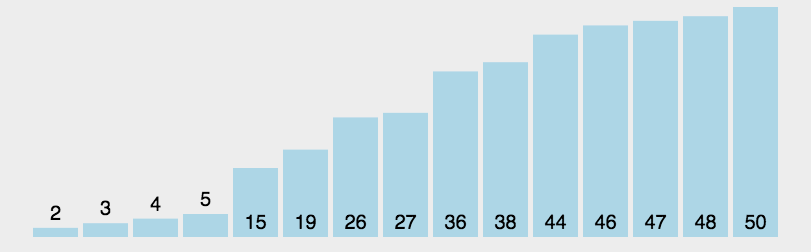
例子

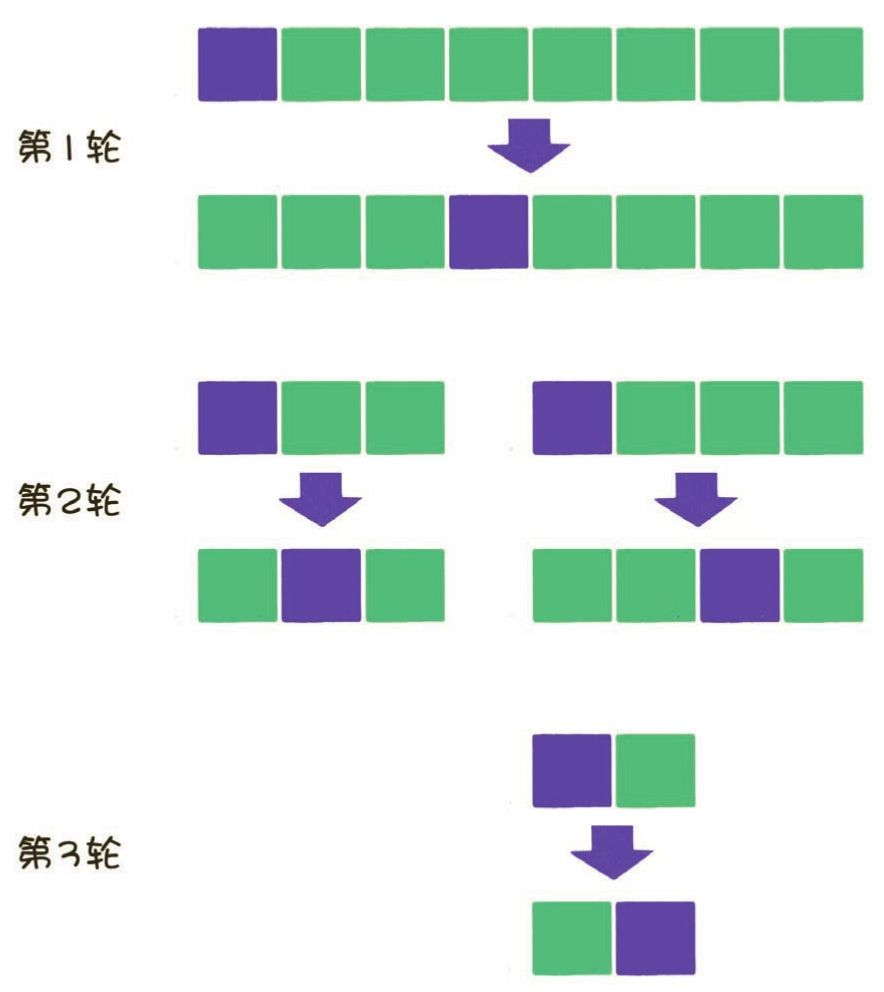
动图展示

基准的选择

先简单介绍一下分治法

将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题来解决，就是分治法

---

基准的选择对于快速排序的时间复杂度影响很大，最坏会使复杂度退化到\(O(n^2)\)

例如：

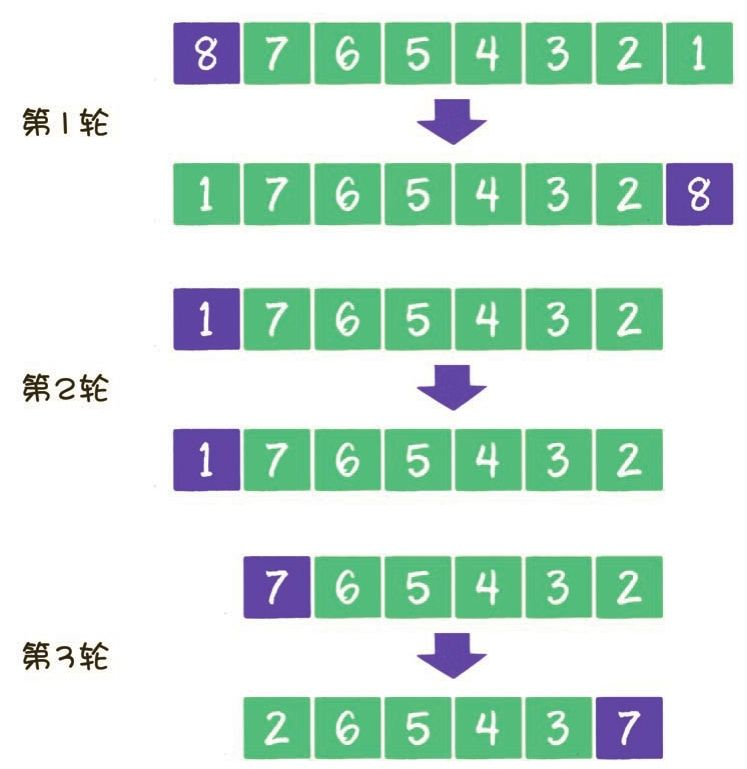
为了避免这种情况发生，可以随机选取一个pivot交换到数列首元素，而不是像动图所展示的直接用首元素

元素的交换

选择好基准 pivot 就可以交换元素了，有两种方法

双边循环法

双边循环法用到两个指针 left 和 right，right指向尾元素，left指向首元素。

1. 从 right 指针开始，让指针所指向的元素和基准元素做比较。如果大于或等于pivot，则指针向左移动；如果小于 pivot，则right指针停止移动，切换到 left 指针。
2. 轮到 left 指针行动，让指针所指向的元素和基准元素做比较。如果小于或等于pivot，则指针向右移动；如果大于 pivot，则 left 指针停止移动。
3. left 与 right 重叠时，重叠位置与 pivot 交换

单边循环发

设置一个 mark 指针指向数列起始位置，这个 mark 指针代表小于基准元素的区域边界。

如果遍历到的元素大于基准元素，就继续往后遍历。如果遍历到的元素小于基准元素，则需要做两件事：

1. 把mark指针右移1位，因为小于 pivot 的区域边界增大了1；
2. 让最新遍历到的元素和mark指针所在位置的元素交换位置，因为最新遍历的元素归属于小于 pivot 的区域。
3. 最后把 pivot 元素于 mark 所指的元素交换

代码

以下代码都是用递归实现的，非递归方法可以用栈实现，可以参考ProgrammerXiaoHui

Java

双边循环

/**
 * 分治（双边循环法）
 * @param arr     待交换的数组
 * @param startIndex    起始下标
 * @param endIndex    结束下标
 */
private static int partition(int[] arr, int startIndex, int endIndex) {
	// 取第一个位置的元素作为基准元素（也可以选择随机位置）
	int pivot = arr[startIndex];
	int left = startIndex;
	int right = endIndex;

	while( left != right) {
		//控制right指针比较并左移
		while(left<right && arr[right] > pivot){
			right--;
		}
		//控制left指针比较并右移
		while( left<right && arr[left] <= pivot) {
			left++;
		}
		//交换left和right指向的元素
		if(left<right) {
			int p = arr[left];
			arr[left] = arr[right];
			arr[right] = p;
		}
	}

	//pivot和指针重合点交换
	arr[startIndex] = arr[left];
	arr[left] = pivot;

	return left;
}

单边循环

/**
 * 分治（单边循环法）
 * @param arr     待交换的数组
 * @param startIndex    起始下标
 * @param endIndex    结束下标
 */
private static int partitionV2(int[] arr, int startIndex, int endIndex) {
	// 取第一个位置的元素作为基准元素（也可以选择随机位置）
	int pivot = arr[startIndex];
	int mark = startIndex;

	for(int i=startIndex+1; i<=endIndex; i++){
		if(arr[i]<pivot){
			mark ++;
			int p = arr[mark];
			arr[mark] = arr[i];
			arr[i] = p;
		}
	}

	arr[startIndex] = arr[mark];
	arr[mark] = pivot;
	return mark;
}

python

def quickSort(arr, left=None, right=None):
    left = 0 if not isinstance(left,(int, float)) else left
    right = len(arr)-1 if not isinstance(right,(int, float)) else right
    if left < right:
        partitionIndex = partition(arr, left, right)
        quickSort(arr, left, partitionIndex-1)
        quickSort(arr, partitionIndex+1, right)
    return arr

def partition(arr, left, right):
    pivot = left
    index = pivot+1
    i = index
    while  i <= right:
        if arr[i] < arr[pivot]:
            swap(arr, i, index)
            index+=1
        i+=1
    swap(arr,pivot,index-1)
    return index-1

def swap(arr, i, j):
    arr[i], arr[j] = arr[j], arr[i]