希尔排序(Shell Sort)

希尔排序

希尔排序(Shell Sort) 是在1959年Shell发明，第一个突破O(n2)的排序算法，是简单插入排序的改进版。它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。

算法描述

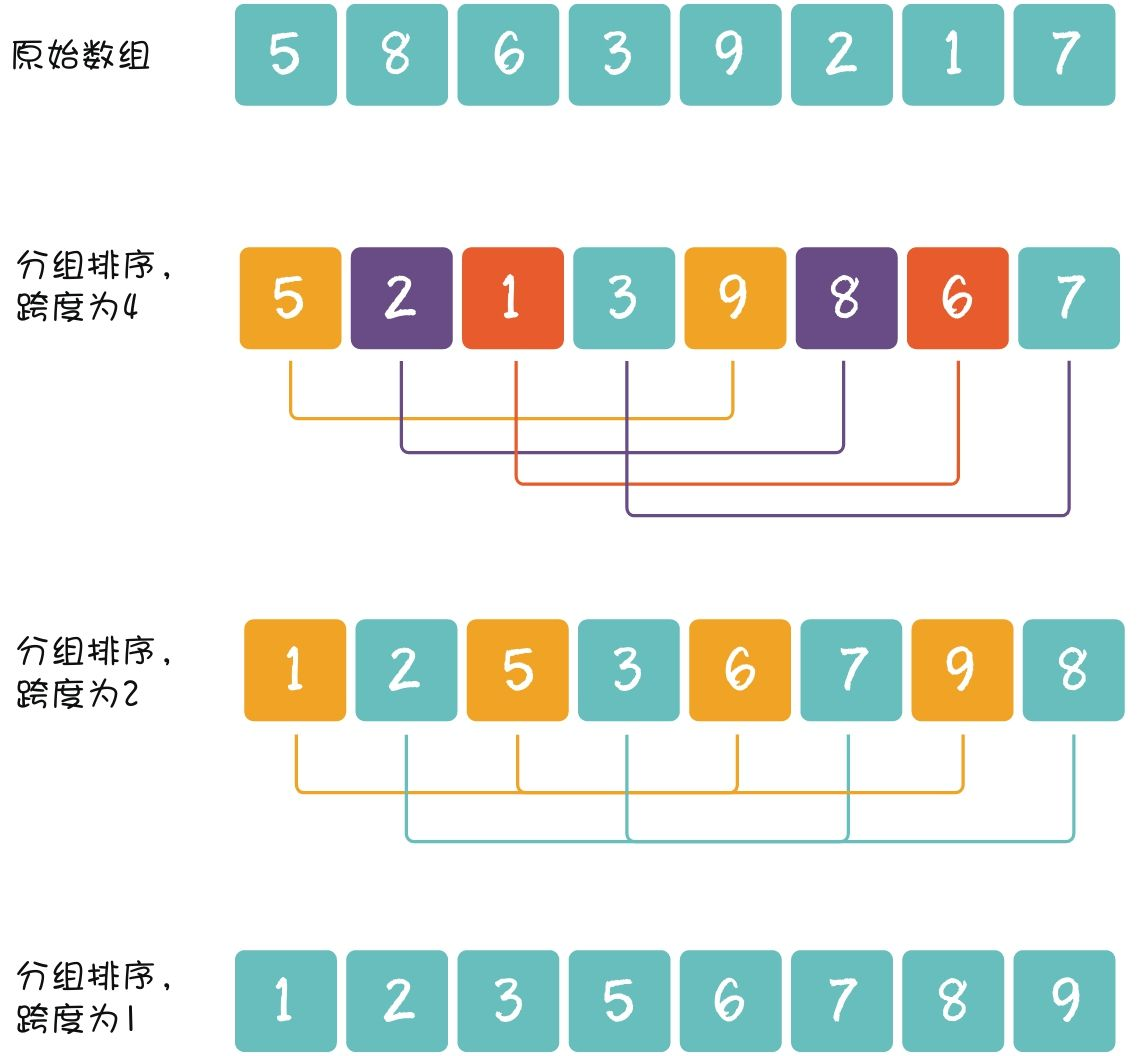
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，具体算法描述：

1. 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
2. 按增量序列个数k，对序列进行k 趟排序；
3. 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

时间复杂度（平均）	时间复杂度（最坏）	时间复杂度（最好）	空间复杂度	稳定性
\(O(n^{1.3})\)	\(O(n^2)\)	\(O(n)\)	\(O(1)\)	不稳定

例子

动图演示

代码

Java

    public static void shellSort(int[] array) {
        //希尔排序的增量
        int d = array.length;

        while (d > 1) {
            //使用希尔增量的方式，即每次折半
            d = d / 2;
            for (int x = 0; x < d; x++) {
                for (int i = x + d; i < array.length; i = i + d) {
                    int temp = array[i];
                    int j;
                    for (j = i - d; (j >= 0) && (array[j] > temp); j = j - d) {
                        array[j + d] = array[j];
                    }
                    array[j + d] = temp;
                }
            }
        }
    }

python

def shellSort(arr):
    import math
    gap=1
    while(gap < len(arr)/3):
        gap = gap*3+1
    while gap > 0:
        for i in range(gap,len(arr)):
            temp = arr[i]
            j = i-gap
            while j >=0 and arr[j] > temp:
                arr[j+gap]=arr[j]
                j-=gap
            arr[j+gap] = temp
        gap = math.floor(gap/3)
    return arr
}

优化

希尔排序中一个重要的值——希尔增量。人们在研究什么样的增量可以避免极端情况。

现在举一个例子具体感受一下极端情况

此时的希尔增量设置为4

这种情况下只有当增量减少到1时数组才会按照插入排序进行，这就是粗调的盲区。

为了保证分组粗调没有盲区，每一轮的增量需要彼此“互质”，也就是没有除1之外的公约数。

例如

1. Hibbard增量：\(1, 3, 7, 15……\)通项公式为\(2k-1\)。利用此种增量方式的希尔排序，最坏时间复杂度是\(O(n^{1.5})\)。
2. Sedgewick增量：\(1, 5, 19, 41, 109……\)通项公式为\(9*4^i-9*2^i+1\)或\(4^i-3*2^i+1\)。利用此种增量方式的希尔排序，最坏时间复杂度是\(O(n^{4/3})\)。