回溯专题其四（排列篇）

一，排列类问题解题思路

排列问题与组合、子集问题的最大不同点在于：排列问题关心元素的顺序。
因此在树形解题空间中，排列类问题会遍历所有可能的顺序，每个元素只能在一个排列中使用一次。

在代码实现上，排列问题常用一个 used 数组来标记当前元素是否已经被选择过，从而避免重复使用。

• 无重复元素的排列（Leetcode 46）：直接通过 used 数组控制元素是否能被选取。
• 有重复元素的排列（Leetcode 47）：在排序的基础上，利用“树层去重”策略（即相同元素只在同一层递归中被选择一次）。

二，具体代码实现

Leetcode题单:

排列 46
排列II 47

1. 排列 46

题目:
给定一个不包含重复元素的序列，返回其所有可能的排列。

Example 1:
Input: nums = [1,2,3]
Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

思路:

• 使用回溯法，逐步构造排列。
• 每次递归都尝试将一个未被使用过的元素加入路径。
• 当路径长度等于数组长度时，即得到一个完整排列。

题目的解空间如下，如图所示，排列问题不使用 startIdx 表示当前循环的起始位置，而是使用 used 数组记录当前元素是否被使用，并跳过使用过的元素

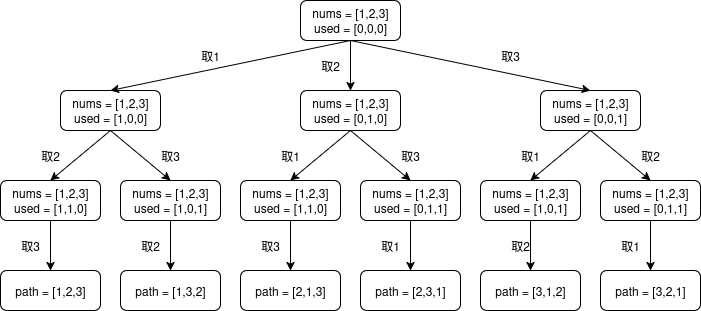
具体代码实现:

class Solution:
    def backtracking(self, nums: List[int], used: List[bool]) -> None:
        if len(self.path) == len(nums):
            self.result.append(self.path.copy())
            return

        for i in range(len(nums)):
            if used[i]:
                continue
            used[i] = True
            self.path.append(nums[i])
            self.backtracking(nums, used)
            self.path.pop()
            used[i] = False

    def permute(self, nums: List[int]) -> List[List[int]]:
        self.path = []
        self.result = []
        used = [False] * len(nums)
        self.backtracking(nums, used)
        return self.result

2. 排列II 47

题目:
给定一个数字序列 nums，其中可能包含重复数字，返回所有可能的排列。

Example 1:
Input: nums = [1,1,2]
Output:
[[1,1,2],
 [1,2,1],
 [2,1,1]]

思路:

• 本质上和全排列相同，但需要处理 重复元素。
• 先对 nums 排序，这样相同元素会相邻。
• 在回溯时加上 树层去重：即如果当前元素与前一个元素相同，且前一个元素在本层未被使用，则跳过当前元素。

具体代码实现:

class Solution:
    def backtracking(self, nums: List[int], used: List[bool]) -> None:
        if len(self.path) == len(nums):
            self.result.append(self.path.copy())
            return

        for i in range(len(nums)):
            if used[i]:
                continue
            # 树层去重
            if i > 0 and nums[i] == nums[i-1] and not used[i-1]:
                continue

            self.path.append(nums[i])
            used[i] = True
            self.backtracking(nums, used)
            used[i] = False
            self.path.pop()

    def permuteUnique(self, nums: List[int]) -> List[List[int]]:
        self.path = []
        self.result = []
        nums.sort()  # 排序方便去重
        used = [False] * len(nums)
        self.backtracking(nums, used)
        return self.result

三，小结

排列问题的关键在于：

• 无重复排列：通过 used 数组控制每个元素只使用一次。
• 有重复排列：在此基础上，结合排序 + 树层去重策略，避免重复解的产生。

与前几类问题（组合、子集、分割）相比，排列类问题更关注 顺序性。
因此，组合/子集问题依赖于 startIdx 约束递归深度，而 排列问题依赖于 used 数组来控制元素使用情况。