回溯专题其二（分割篇）

一、分割类问题解题思路

分割类问题的特点是：

• 我们需要在字符串中不断尝试放置“分割线”；
• 每个切分后得到的子串必须满足一定条件；
• 当分割线走到字符串末尾时，得到一个完整的方案。

因此，这类问题可以抽象为 在字符串中选择切割点的过程，也可以看作一类特殊的组合问题
回溯函数的核心参数通常是 当前分割线的起始位置 startIdx，递归结束条件是 startIdx 到达字符串末尾。

整体框架依然是“回溯三部曲”：

1. 参数与返回值：参数包含原始字符串、起始位置等；返回值为空，结果存到全局变量。
2. 递归终止条件：当分割线到达末尾，说明当前切分方案合法，加入结果。
3. 单层递归逻辑：尝试在不同位置切割，判断子串是否合法，合法则递归下探，否则跳过。

---

二、具体代码实现

LeetCode 题单:

- **分割回文串 131**
- **复原IP地址 93**

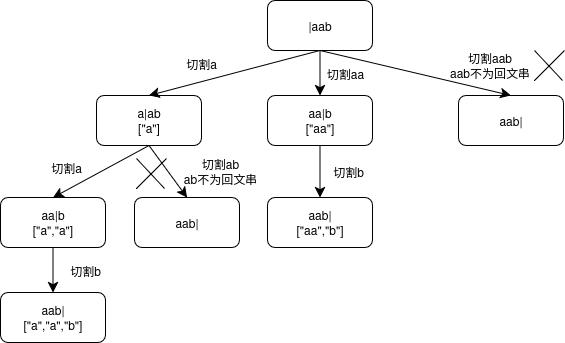
1. 分割回文串 131

题目:
给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。
返回所有可能的分割方案。

示例：
输入: "aab"
输出: [["aa","b"], ["a","a","b"]]

思路:

• 递归参数：除了字符串自身 s 外，使用 startIdx 表示当前切割起点。
• 终止条件：当 startIdx 到达末尾，说明得到了一种分割方案，加入结果。
• 单层逻辑：从 startIdx 到末尾，依次尝试切割；若当前子串是回文串，则继续递归；否则跳过。

class Solution:
    def isPalindrome(self, s: str, startIdx: int, endIdx: int) -> bool:
        # 判断子串是否为回文串（左闭右闭区间）
        while startIdx < endIdx:
            if s[startIdx] != s[endIdx]:
                return False
            startIdx += 1
            endIdx -= 1
        return True

    def backtracking(self, s: str, startIdx: int) -> None:
        if startIdx >= len(s):
            self.result.append(self.path.copy())
            return

        for i in range(startIdx, len(s)):
            # 只有当前子串是回文时，才继续递归
            if self.isPalindrome(s, startIdx, i):
                self.path.append(s[startIdx:i+1])
                self.backtracking(s, i+1)
                self.path.pop()

    def partition(self, s: str) -> List[List[str]]:
        self.result = []
        self.path = []
        self.backtracking(s, 0)
        return self.result

2. 复原IP地址 93

题目:
给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。

有效的 IP 地址：

• 恰好由四段数字组成，每段在 0~255 范围内；
• 不能有前导零；
• 用 . 分隔。

示例：
输入: "25525511135"
输出: ["255.255.11.135", "255.255.111.35"]

思路:

• 递归参数：startIdx 表示当前段的起始位置，另用 dotCount 统计已放置的分隔符数。
• 终止条件：当分隔符数为 3 且最后一段合法时，说明是一个有效 IP，加入结果。
• 单层逻辑：尝试切分长度为 1~3 的子串，判断其是否在 0~255 且无前导零，合法则递归下探。

class Solution:
    def isValidIP(self, s: str, startIdx: int, endIdx: int) -> bool:
        # 左闭右闭区间
        if startIdx > endIdx:
            return False

        # 判断当前片段中是否存在前导0
        if s[startIdx] == '0' and startIdx != endIdx:
            return False

        # 判断对应整数范围是否在0-255之间
        val = int(s[startIdx:endIdx+1])
        if val >= 0 and val <= 255:
            return True
        return False

    def backtracking(self, s: str, startIdx: int, dotNum: int) -> None:
        # 已经添加了三个分割点，分割了三份。需要判断字符串剩余的部分是否符合IP地址的要求
        if dotNum == 3:
            if self.isValidIP(s, startIdx, len(s)-1):
                self.path.append(s[startIdx:])
                self.result.append('.'.join(self.path))
                self.path.pop()
            return

        for i in range(startIdx, len(s)):
            if not self.isValidIP(s, startIdx, i):
                break
            self.path.append(s[startIdx:i+1])
            self.backtracking(s, i+1, dotNum+1)
            self.path.pop()

    def restoreIpAddresses(self, s: str) -> List[str]:
        self.result = []
        self.path = []
        if len(s) >= 4 and len(s) <= 12:
            self.backtracking(s, 0, 0)
        return self.result

---

三、小结

分割类问题的核心在于 如何合理地切分字符串：

• 131. 分割回文串：切分后要求每一段都是回文串。
• 93. 复原 IP 地址：切分后要求每一段满足数值范围且无前导零。

二者的共同点是：

• 都以 startIdx 为切割起点；
• 都在每一层尝试不同的切割点；
• 只有满足条件的子串才会继续递归。

区别则在于 子串合法性的判断逻辑：

• 回文串通过“左右双指针”判断；
• IP 段通过“前导零检查 + 数值范围”判断。

从框架上看，这类问题与组合问题如出一辙：

• 组合是 在集合中选数；
• 分割是 在字符串中切点。
  所不同的 只是约束条件。