回溯专题其一（组合篇）

一、回溯理论基础

回溯的概念

回溯（Backtracking）是一种搜索算法，常被称为“回溯搜索”。它本质上是 递归的副产品：在递归过程中不断尝试不同的选择，当某条路径不满足条件时，就 回退到上一步重新选择。因此，有回溯必有递归。

由于回溯法会枚举搜索空间中的所有可能路径（可通过剪枝优化减少无效搜索），它非常适合解决 枚举子集、组合或排列 等类问题。这些问题往往难以用动态规划或贪心等常规解法解决。

抽象来看：

集合的大小 → 决定了树的宽度
递归深度 → 决定了树的深度

常见应用场景：

组合问题：N 个数中找出 K 个数的集合
切割问题：字符串的切割方式
子集问题：求所有满足条件的子集
排列问题：生成所有排列
棋盘问题：N 皇后、数独等

回溯法模板

和递归类似，回溯也可以总结为“三部曲”：

回溯函数的参数与返回值
- 返回值一般为空，结果保存到全局变量中
- 参数根据题目不同，可能包括目标值、集合、起始索引等
递归终止条件
- 每次递归对应树的一层，总会有终止条件
- 一般是“找到一个符合条件的解” → 保存结果并返回

if condition:
    result.append(path.copy())
    return

单层递归逻辑
- 横向：for 循环遍历当前层的可选元素
- 纵向：进入递归，继续深入
- 回退：撤销选择，恢复现场

for 选择本层集合中的元素:
    做出选择
    backtracking()
    撤销选择

完整模板：

def backtracking(参数):
    if condition:
        result.append(path.copy())
        return
    for 选择本层集合中的元素:
        path.append(元素)      # 做出选择
        backtracking(...)      # 递归
        path.pop()             # 撤销选择

二、组合类问题的解题思路

LeetCode 常见题目：

组合 77
组合总和 III 216
电话号码的字母组合 17
组合总和 39
组合总和 II 40

我们以 LeetCode 77. 组合 为例，来说明组合类问题的分析思路。

题目：给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数组合。
示例：输入 n=4, k=2，输出：
[[2,4], [3,4], [2,3], [1,2], [1,3], [1,4]]

树形结构分析

我们可以将组合问题抽象为树形结构，每层选择一个数字：

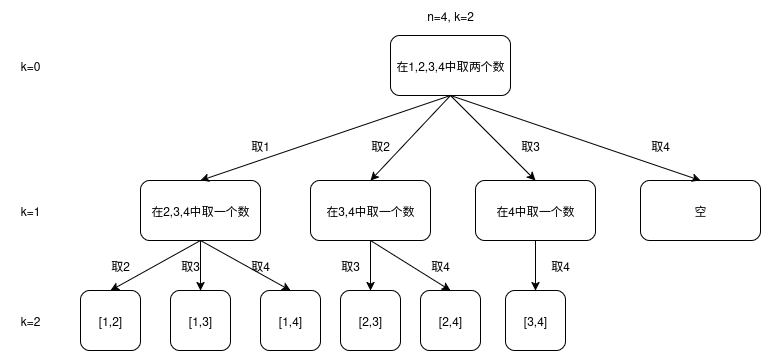
n 控制树的宽度
k 控制树的深度
当路径长度等于 k 时，得到一个完整解，保存后结束递归

回溯三部曲应用

参数与返回值
参数包括 n、k，以及 startIdx，用于限制下层循环的起始位置，避免重复组合。
返回值为空，结果存入全局变量 result，当前路径用 path 保存。
递归终止条件

if len(path) == k:
    result.append(path.copy())
    return

单层搜索逻辑
在当前层，从 startIdx 开始遍历所有候选数，依次加入路径，递归下探，再回溯撤销。

for i in range(startIdx, n+1):  # 横向遍历
    path.append(i)              # 做出选择
    backtracking(n, k, i+1)     # 递归
    path.pop()                  # 撤销选择

三、具体代码实现

1. 组合 77

有了以上的思路铺垫，给出组合 77的实现代码
剪枝前：

class Solution:
    def backtracking(self, n: int, k: int, startIdx: int) -> None:
        if len(self.path) == k:
            self.result.append(self.path.copy())
            return

        for i in range(startIdx, n):
            self.path.append(i+1)
            self.backtracking(n, k, i+1)
            self.path.pop()

    def combine(self, n: int, k: int) -> List[List[int]]:
        self.result = []
        self.path = []
        self.backtracking(n, k, 0)
        return self.result

剪枝后：

如果剩余可选数字数量不足以补齐 k，则提前终止搜索：

class Solution:
    def backtracking(self, n: int, k: int, startIdx: int) -> None:
        if len(self.path) == k:
            self.result.append(self.path.copy())
            return

        for i in range(startIdx, n - (k - len(self.path)) + 1):  # 剪枝
            self.path.append(i+1)
            self.backtracking(n, k, i+1)
            self.path.pop()

    def combine(self, n: int, k: int) -> List[List[int]]:
        self.result = []
        self.path = []
        self.backtracking(n, k, 0)
        return self.result

2. 组合总和 III 216

题目：找出所有相加之和为 n 的 k 个数组合。只能用 1-9 的数字，每个数字最多用一次。

示例：

输入：k=3, n=7 → 输出 [[1,2,4]]
输入：k=3, n=9 → 输出 [[1,2,6], [1,3,5], [2,3,4]]

思路：

参数：目标和 n，组合长度 k，树层起始索引 startIdx
终止条件：路径长度 = k 时检查和是否等于 n
单层搜索：从 startIdx 开始遍历 1-9，选一个数加入路径，再递归

代码实现：

class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        self.path = []
        self.result = []
        self.backtracking(k, n, 1)
        return self.result

    def backtracking(self, k: int, n: int, startIdx: int) -> None:
        if len(self.path) == k:
            if n == 0:
                self.result.append(self.path.copy())
            return

        endIdx = min(n + 1, 10)  # 剪枝：数字不会超过 n 或 9

        for i in range(startIdx, endIdx):
            if n - i < 0:  # 剪枝：和已超出目标
                break

            self.path.append(i)
            self.backtracking(k, n - i, i + 1)
            self.path.pop()

3. 电话号码的字母组合 17

题目：给定数字 2-9，返回所有可能的字母组合。

映射关系：

2 -> abc
3 -> def
4 -> ghi
5 -> jkl
6 -> mno
7 -> pqrs
8 -> tuv
9 -> wxyz

思路：

参数：数字字符串 digits，当前递归深度 index
终止条件：当 index == len(digits)，收集路径
单层搜索：取出当前数字对应的字母串，依次尝试

代码实现：

class Solution:
    letterMap = {
        '2': 'abc', '3': 'def', '4': 'ghi', '5': 'jkl',
        '6': 'mno', '7': 'pqrs', '8': 'tuv', '9': 'wxyz'
    }

    def backtracking(self, digits: str, index: int) -> None:
        if index == len(digits):
            self.result.append(''.join(self.path))
            return

        letters = self.letterMap[digits[index]]
        for ch in letters:
            self.path.append(ch)
            self.backtracking(digits, index + 1)
            self.path.pop()

    def letterCombinations(self, digits: str) -> List[str]:
        self.path = []
        self.result = []
        if digits:
            self.backtracking(digits, 0)
        return self.result

4. 组合总和 39

题目：在 candidates 中找到和为 target 的所有组合，数字可重复使用。

示例：
输入：candidates = [2,3,6,7], target = 7
输出：[[7], [2,2,3]]

思路：

元素可以重复使用，所以递归时仍然传入当前索引 i
剪枝：如果当前和超过 target，直接返回
搜索时要先排序，以便提前终止循环

代码实现：

class Solution:
    def backtracking(self, candidates: List[int], target: int, startIdx: int, sum: int) -> None:
        if sum == target:
            self.result.append(self.path.copy())
            return

        for i in range(startIdx, len(candidates)):
            if sum + candidates[i] > target:  # 剪枝
                break
            self.path.append(candidates[i])
            self.backtracking(candidates, target, i, sum + candidates[i])
            self.path.pop()

    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        self.path = []
        self.result = []
        candidates.sort()
        self.backtracking(candidates, target, 0, 0)
        return self.result

5. 组合总和 II 40

题目：在 candidates 中找到和为 target 的所有组合，每个数字只能使用一次，数组可能有重复。

示例：
输入：candidates = [10,1,2,7,6,1,5], target = 8
输出：[[1,7], [1,2,5], [2,6], [1,1,6]]

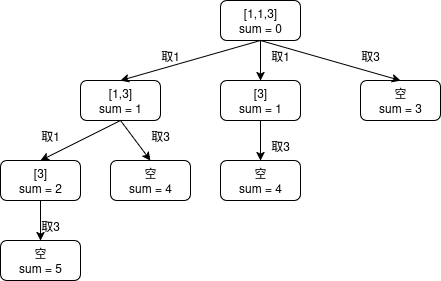
思路：

每个数字只能用一次 → 递归时传 i+1
数组可能重复 → 在同一层中对相同元素去重
去重方式：排序 + used 数组，若前一个相同元素未被使用，则跳过当前元素

代码实现：

class Solution:
    def backtracking(self, candidates: List[int], target: int, startIdx: int, sum: int, used: List[bool]) -> None:
        if sum == target:
            self.result.append(self.path.copy())
            return

        for i in range(startIdx, len(candidates)):
            if sum + candidates[i] > target:  # 剪枝
                break
            if i > 0 and candidates[i] == candidates[i-1] and not used[i-1]:
                continue  # 同层去重

            self.path.append(candidates[i])
            used[i] = True
            self.backtracking(candidates, target, i+1, sum+candidates[i], used)
            self.path.pop()
            used[i] = False

    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        used = [False]*len(candidates)
        self.path = []
        self.result = []
        candidates.sort()
        self.backtracking(candidates, target, 0, 0, used)
        return self.result

四，小结

以上五道题目本质上都属于回溯的组合类问题，核心逻辑都是：

用一个 path 保存当前组合
用 result 收集所有解
通过递归 + 回溯遍历解空间

它们的主要区别在于约束条件的不同：77. 组合：从 1..n 中选 k 个数，无和限制 216. 组合总和 III：固定选 k 个数，且和为 n，数字范围 1..9 17. 电话号码字母组合：典型的多叉树遍历，层数由输入长度决定 39. 组合总和：可重复使用数组中的元素，求和为 target 40. 组合总和 II：与 39 类似，但每个数只能用一次，并需要处理数组中的重复元素

可以看到，这些题目的解法都是在统一回溯框架下，稍作改动即可适配：

通过剪枝提高效率
通过索引控制或 used 数组来避免重复
通过限制路径和或路径长度来满足题目条件

posted @ 2025-08-31 11:47 雪痕春风天音九重色阅读(0) 评论(0) 收藏举报

刷新页面返回顶部

moonlightgreatsword

回溯专题其一（组合篇）

一、回溯理论基础

回溯的概念

回溯法模板

二、组合类问题的解题思路

树形结构分析

回溯三部曲应用

三、具体代码实现

1. 组合 77

2. 组合总和 III 216

3. 电话号码的字母组合 17

4. 组合总和 39

5. 组合总和 II 40

四，小结

公告