代码随想录算法训练营第十三天(二叉树篇)|Leetcode110平衡二叉树,Leetcode257二叉树的所有路径,Leetcode404左叶子之和,Leetcode222完全二叉树的节点个数
Leetcode 110 平衡二叉树
题目链接: 平衡二叉树
给定一棵二叉树,检查该二叉树是否为高度平衡的。
所谓高度平衡的二叉树,即为二叉树左右子树的高度差不大于1
思路: 本题通过递归法求解。
利用递归三部曲进行分析:
- 递归函数参数与返回值
递归函数的参数为当前遍历的节点;返回值为一个整数,即以当前节点为根节点的二叉树的深度,若已经判断以当前节点为根节点的子树不符合平衡二叉树的要求,则直接返回-1 - 递归终止条件
当前节点为空节点时,返回0 - 每层递归完成的操作
判断当前节点的左右子树深度的差值是否大于1, 若否,则向上返回以当前节点为根节点的子树的深度;若是,则直接返回-1
具体代码实现:
class Solution:
def getDepth(self, cur: Optional[TreeNode]) -> int:
if cur is None:
return 0
leftDepth = self.getDepth(cur.left)
rightDepth = self.getDepth(cur.right)
if leftDepth == -1 or rightDepth == -1 or abs(leftDepth - rightDepth) > 1:
return -1
return 1 + max(leftDepth, rightDepth)
def isBalanced(self, root: Optional[TreeNode]) -> bool:
return False if self.getDepth(root) == -1 else True
Leetcode 257 二叉树的所有路径
题目链接: 二叉树的所有路径
给定一棵二叉树的根节点,以任意次序返回该二叉树从根节点到叶子节点的所有路径
Example1:
1
/ \
2 3
\
5
Input: root = [1,2,3,null,5]
Output: ["1->2->5","1->3"]
思路: 涉及到二叉树中路径的问题,往往需要配合回溯加以解决。关于回溯的思想,后续在回溯章节中会详细阐述。此处把回溯理解为: 回撤先前的操作,选择一条与先前不同的道路即可。
如以上示例中,首先将根节点 1 加入路径中,随后将左子节点 2 加入路径中,最后是叶子节点 5,找出一条路径。随后,要将路径中已有的 5 和 2 从路径中移出,再将右子节点 3 加入到路径中,找出第二条路径。回溯的关键在于回退先前的操作。
有了以上理论基础后,我们对题目进行递归三部曲分析:
- 递归函数参数与返回值
递归函数参数为当前二叉树中当前遍历的节点,以及一个存放结果路径的列表,返回值为空 - 递归终止条件:
当前节点的两个子节点均为空节点时(即当前节点为叶子节点时)终止递归,将当前路径加入到结果列表中 - 每层递归所做操作:
判断当前节点是否存在子节点,若存在,则触发相应递归函数,获取相应路径(注意回溯)
具体代码实现
class Solution:
def getPath(self, cur: Optional[TreeNode], path: List[str], result: List[str]) -> None:
# 当前节点一定不为空,先将当前节点的值加入到路径中
path.append(str(cur.val))
# 当前节点为叶子节点,将当前路径加入到结果列表
if cur.left is None and cur.right is None:
result.append('->'.join(path))
return
else:
# 左节点存在,获取左节点相应路径
if cur.left:
self.getPath(cur.left, path, result)
path.pop() # 路径弹出左节点的值,完成回溯操作
if cur.right:
self.getPath(cur.right, path, result)
path.pop()
def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
path = []
result = []
if root is None:
return result
self.getPath(root, path, result)
return result
Leetcode 404 左叶子之和
题目链接: 左叶子之和
给定一棵二叉树的根节点,返回其所有左叶子节点之和。左叶子节点的定义为,该节点为某个节点的左侧叶子节点。
思路: 利用递归三部曲进行分析
- 递归函数的参数为当前正在遍历的节点,返回值为以当前节点为根节点的子树部分中,左叶子节点的总和
- 若当前节点为空节点时返回 0,若当前节点为左叶子节点时,返回当前节点的值
- 汇总当前节点左子树和右子树中左叶子节点之和
具体代码实现
class Solution:
def getSumOfLeftLeaves(self, cur: Optional[TreeNode]) -> int:
if cur is None:
return 0
# 当前节点的左孩子节点为左叶子节点
if cur.left and cur.left.left is None and cur.left.right is None:
return cur.left.val + self.getSumOfLeftLeaves(cur.right)
# 汇总当前节点左子树和右子树中左叶子节点之和
return self.getSumOfLeftLeaves(cur.left) + self.getSumOfLeftLeaves(cur.right)
def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
return self.getSumOfLeftLeaves(root)
Leetcode 222 完全二叉树的节点个数
题目链接: 完全二叉树的节点个数
给定一棵完全二叉树的根节点,要求返回其中节点的个数。
思路: 最简单直接的思路是直接遍历整棵二叉树,统计节点的数量,时间复杂度为 O(n)。但是这样没有利用上完全二叉树的特性,显然不是最优解。
首先复习下概念。
完全二叉树的定义为: 在一颗二叉树中,若除最后一层外的其余层都是满的,并且最后一层要么是满的,要么在右边缺少连续若干节点,则此二叉树为完全二叉树(Complete Binary Tree)
满二叉树的定义为:
在一棵二叉树中,每个节点都要么有0个子节点,要么有2个子节点,则这种二叉树称作满二叉树(Full Binary Tree)
可以发现,完全二叉树若把最后一层填满,则能够转换为满二叉树。满二叉树为完全二叉树的一种特殊情况。
满二叉树的节点计算公式为 $2^{depth}-1$,这样,我们可以通过统计满二叉树的高度,实现满二叉树节点的快速统计。
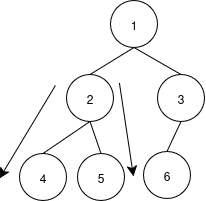
可以看到,完全二叉树中存在局部片段符合满二叉树的性质。因此,我们可以在完全二叉树中递归地判断当前片段是否为满二叉树,若是,则可以直接通过其深度计算出其中相应的节点个数。
利用递归三部曲进行分析:
- 递归函数的参数与返回值:
递归函数的参数为当前正在遍历的节点,返回值为一个整数,即以该节点为根节点,对应的子树部分的节点数量 - 递归终止条件:
当前节点的最左叶子节点与最右叶子节点的深度相同时,即可以说明当前节点为根节点的部分子树为满二叉树。此时终止递归操作,并返回相应的节点数量。 - 每层递归所做的操作:
计算以当前节点为根节点的子树中,相应的节点数量之和。
具体代码实现
class Solution:
def getCount(self, cur: Optional[TreeNode]) -> int:
if cur is None:
return 0
leftDepth, rightDepth = 1, 1
leftNode, rightNode = cur.left, cur.right
while leftNode:
leftDepth += 1
leftNode = leftNode.left
while rightNode:
rightDepth += 1
rightNode = rightNode.right
# 当前节点的最左叶子节点与最右叶子节点的深度相同,说明相应片段为满二叉树
if leftDepth == rightDepth:
return 2 ** rightDepth - 1
return 1 + self.getCount(cur.left) + self.getCount(cur.right)
def countNodes(self, root: Optional[TreeNode]) -> int:
return self.getCount(root)
时间复杂度: O(logn)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号