最小二乘法
1、前言
a、本文主性最小二乘的标准形式，非线性最小二乘求解可以参考Newton法
b、对于参数求解问题还有另外一种思路：RANSAC算法。它与最小二乘各有优缺点：
--当测量值符合高斯分布（或者说测量误差符合期望为0的高斯分布），使用最小二乘比较合适，可以获得比较稳定且很高的精度。
而当误差服从高斯分布的情况下， 最小二乘法等价于极大似然估计。
--当测量值离散性比较大，存在很多outliers，那么使用最小二乘求解就会存在很大的误差，此时使用RANSAC算法更合适。
线性最小二乘只适用于参数模型会线性关系的情形，RANSAC则没有此限制。
c、线性最小二乘又分为齐次线性最小二乘和非齐次线性最小二乘。
2、非齐次方程组的最小二乘解
a、非齐次线性最小二乘的标准形式：
AX = B (1)
其中A、B分别为测量数据构成的矩阵与向量，X为待求参数向量。这里主要针对方程数多于未知元素的情形--超定方程组。
b、为什么要用最小二乘求解参数：
举例：
，其中
为测量已知量，
为待求量。
那么只需要三组
如何在（1,2,3,29）（2,1,1,13）（3,2,4,37）（2,4,2,33）（4,2,1,23）这些测量数据中求出最准确的
结论：当数据存在冗余，且数据噪声偏差不大的情况下适合用最小二乘求解。
c、如何转化为最小二乘形式：
例1：y = ax+b，已知（x,y）求（a,b）？
转化为标准形式：
![[x,1]\left[{\begin{array}{*{20}{c}}
a\\
b
\end{array}}\right]=\left[y\right]](http://latex.codecogs.com/gif.latex?%5bx%2c1%5d%5cleft%5b%7b%5cbegin%7barray%7d%7b*%7b20%7d%7bc%7d%7d%0aa%5c%5c%0ab%0a%5cend%7barray%7d%7d%5cright%5d%3d%5cleft%5by%5cright%5d)
带入测量数据：
![\left[{\begin{array}{*{20}{c}}
{{x_1}}&1\\
{{x_2}}&1\\
{{x_3}}&1\\
{{x_4}}&1
\end{array}}\right]\left[{\begin{array}{*{20}{c}}
a\\
b
\end{array}}\right]=\left[{\begin{array}{*{20}{c}}
{{y_1}}\\
{{y_2}}\\
{{y_3}}\\
{{y_4}}
\end{array}}\right]](http://latex.codecogs.com/gif.latex?%5cleft%5b%7b%5cbegin%7barray%7d%7b*%7b20%7d%7bc%7d%7d%0a%7b%7bx_1%7d%7d%261%5c%5c%0a%7b%7bx_2%7d%7d%261%5c%5c%0a%7b%7bx_3%7d%7d%261%5c%5c%0a%7b%7bx_4%7d%7d%261%0a%5cend%7barray%7d%7d%5cright%5d%5cleft%5b%7b%5cbegin%7barray%7d%7b*%7b20%7d%7bc%7d%7d%0aa%5c%5c%0ab%0a%5cend%7barray%7d%7d%5cright%5d%3d%5cleft%5b%7b%5cbegin%7barray%7d%7b*%7b20%7d%7bc%7d%7d%0a%7b%7by_1%7d%7d%5c%5c%0a%7b%7by_2%7d%7d%5c%5c%0a%7b%7by_3%7d%7d%5c%5c%0a%7b%7by_4%7d%7d%0a%5cend%7barray%7d%7d%5cright%5d)
例2：
，已知
，求（a,b）？
转化为标准形式：
带入测量数据：
例3：
，
求
？？
转化为标准形式：
带入测量数据：
总结：对于线性表达式，通过适当的变型即可，如例1。
在例2中，通过选取
和
为基实现了线性化。
对于非线性表达式，可以通过合适的基、变型，有时候也可以转化为标准形式，如例2、例3。
在例3中，对参数p矩阵选取合适的基实现了线性化。
即选取基：
、
、
、
、
、
那么矩阵p在该组基下：
c、标准形式下最小二乘的求解：
对于（1）式，最小二乘的求解，相当于求解正规方程：
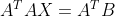
标准形式下最小二乘解为：
%5e%7b-1%7d%7d%7bA%5eT%7dB)
d、证明：
方法1：
AX = B ，对于实际测量数据，(AX – B)，即残差将不为0，为了得到最准确的解，应使残差的范数最小：
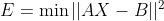
对E展开：
令E的导数等于0，即可求出X:
方法2：
根据（4）式 （B - AX）所构成的向量需要垂直于A的列空间，此时距离最短，E最小：
A（AX - B）= 0 （5）
根据（5）式：
3、齐次方程组的最小二乘解
a、齐次线性最小二乘的标准形式：
AX = 0 (6)
其中A为测量数据构成的矩阵与向量，X为待求参数向量。
这里主要针对方程数多于未知元素的情形--超定方程组。
这个模型和
是等价的。
b、齐次方程组的最小二乘解的约束
因平凡解 X = 0不是我们感兴趣的解，因此我们主要是寻求该方程组的非零解。
注意，如果 X 是这个方程组的解，那么对于任何标量k，使得kX也是解，因此可以建立一个合理的约束：||X||=1的解：
齐次最小二乘相当于求解：
或者求解：
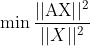
c、齐次方程组的最小二乘解
通过前面a、b两部分的说明，此时问题的标准形式为：求使||AX||最小化并满足||X|| = 1时的X。其结论为：
最小特征值对应的特征向量即为待求解
证明：
对A矩阵SVD分解（可参加我另外一篇博客），令
，那么问题变成：
且
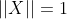
由于：
，即U矩阵不影响范数。
同时：
，和U矩阵一样，V矩阵不影响范数。
那么（7）式变为：
且
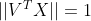
令 ||y|| = 1，则（8）式变为：
且
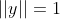
由SVD分解的规则可知，D是对角元素按降序排列的一个对角矩阵，
因此该问题的解是
，它具有一个非零元素1并在最后的位置上。
就是V的最后一列。
4、加权最小二乘问题
这是对非齐次方程组的最小二乘问题的补充。
对于每一组测量数据，都存在（4）式所定义的误差E，当对不同的E进行加权时，便成了加权最小二乘问题。
此时，（5）式应变为：
，（2）应变为：
，其中C为加权矩阵。
加权最小二乘问题的解为：
5.1、带约束方程组的最小二乘解（1）
如果3、齐次方程组的最小二乘模型存在约束，即：
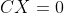
求解思路分析：
对C矩阵进行SVD分解，
，如果C不是方阵，如何行数少于列数那就在C矩阵后面一行行补0。
如果对角矩阵D有r个非零对角元素，此时C的秩为 r 且C的行空间由
的前 r 行生成，则C的行空间的正交补
由
余下的行生成，记
的消去前 r 列得到的矩阵，则
，对比
X的解由
。
由于
此时，（10）变成：
且
（10）求解算法总结：
a、如果C的行数少于列数，则在C矩阵的后面添加若干行0从而扩展成方阵，通过对C进行SVD分解，求出
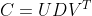
b、分解的时候将非零元素排在D矩阵的前面，将矩阵V消去前 r 列（r为D矩阵对角线上非零元素个数）得到矩阵
c、根据3、齐次方程组的最小二乘模型的求解方法求解（11）。
5.2、带约束方程组的最小二乘解（2）
5.3、带约束方程组的最小二乘解（3）
