二叉树与树

树形结构

• 一个结构不空，其中就存在这唯一的起始结点，称为树根（root）
• 按结构的连接关系，树根外的其余结点都有且只有 一个前驱，但另一方面，一个结点可以有 0个或者多个后继，另外，在非空的树结构中一定有写结点并不连接到其他结点，这种结点与表的尾结点性质类似，但一个树结构里可以存在多个 这种结点
• 结构里的所有结点都 在树根结点通过后继关系可达的结点集合里，换句话说，从树根结点出发，经过若干次后继关系可以达到结构中的任意结点。
• 从这种结构 里的任意两个 不同结点出发，通过后继关系可达的两个结点的几个，或者互不相交，或者一个集合是另一个集合的子集

二叉树

• 二叉树是一种最简单的树形结构，其特点是树中每个结点之多 关联到两个后继结点，也就是说，一个结点的关联结点数可以 是0，1或2。另一个特点是一个结点关联的后继结点明确地分左右，或为其左关联结点，或为其右关联结点。
• 二叉树定义：二叉树是结点的有穷集合，这个集合或者是空集，或者其中有一个称为根节点的特殊结点，其余结点分数两棵不相交 的 二叉树，这两颗二叉树分别是原二叉树（或者说是原二叉树的根节点）的左子树和右子树
• 如图所示，途中给出了几种二叉树，其中左边一棵树比较符合直观，根结点有两棵子树，具有一层层 的结构；中间是一棵只包含根结点的二叉树；右边也是一棵二叉树，但其每个结点都只有一棵右子树
• 
• 概念：
  • 不包含任何结点的二叉树称为空树
  • 只包含一个结点的二叉树是一棵单点树
  • 一般而言 ，一棵二叉树可以包含任一个结点
  • 一棵二叉树的根节点称为该树的子树根结点的父结点，与之对应，子树的根节点称为二叉树树根结点的子节点，父结点与子节点的概念是相对的
  • 可认为从父结点到子结点有一条连线，称为从父结点到子结点的边，注意，这种边有方向，形成一种单方向的父结点/子结点关系。基于父子关系可以定义其传递关系，称为祖先/子孙关系，它决定一个结点的祖先结点，或子孙结点。父结点相同的两个结点互为兄弟结点。
  • 在二叉树里有些结点的两棵子树 都空，没有子结点，这种结点称为树叶（结点）。书中其余 结点 称为分支结点
  • 一个结点的子结点个数称为该结点的度数，显然，二叉树中树叶结点的度数为0，分支结点的度数是 1或者2
• 路径：从一个祖先结点到其任何子孙结点都存在一系列边，形成从前者到后者的联系，这样一些列首尾相连的边称为树中的一条路径，路径中边的条数称为该路径的长度，显然，从一个结点到其子结点有一条长度为1的路径，每个结点到其自身有一条长度为0的路径
• 层：二叉树是一种层次结构，将其树根看作最高层元素，如果有子结点，其子结点看作下一层元素，规定二叉树树根层数为0，对位于k层的结点，其子结点是k+1层元素，如此下去，二叉树的所有结点可以按这种关系分为一层层元素，易见，从树根到任一结点的路径长度就是该结点所在 的层数，也称为该节点的层数
• 高度：一棵二叉树的高度（也称为深度）是树中结点的最大层数，也就是这棵树里最长路径的长度，树的高度是二叉树的整体性质，只有根节点的树高度为0

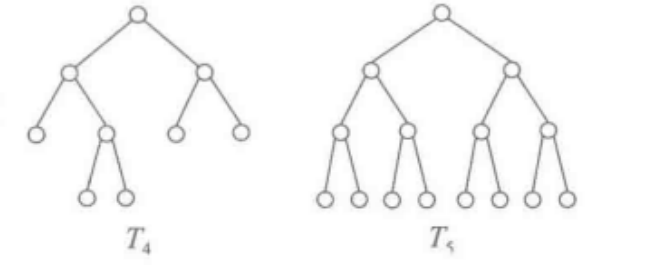
满二叉树：如果二叉树 中所有 分支结点的度数都是2，则称它为一棵满二叉树。满二叉树是一般二叉树的一个子集，如图所示：

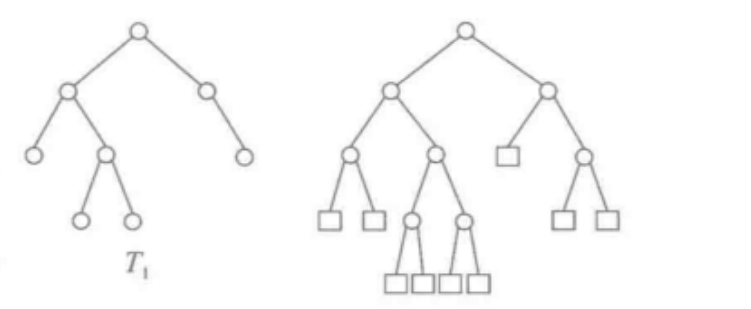
扩充二叉树：对二叉树T,加入足够多的新叶结点，使T的原有结点都边称度数为2的分支结点，得到的二叉树称为T的扩充二叉树，扩充二叉树中新增的结点称为外部结点，原树T的结点称为内部结点，空树的扩展二叉树规定为空树。如下图所示：

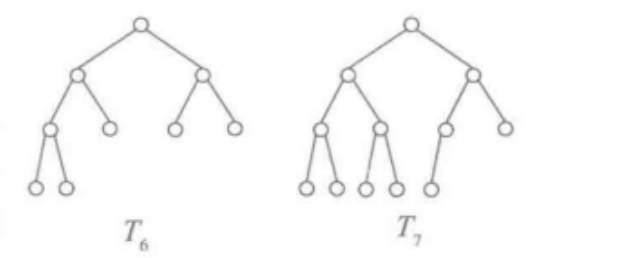
完全二叉树：对于 一棵高度为 h的二叉树，如果其第0层至第h-1层的结点都满 ，也就是说，对所有0<=i<=h-1，第i层都有两个结点，如果下一层的结点不满，则所有结点在最左边连续排列，空位都在最右边，这样的二叉树就是一个完全二叉树。如图

下面是一个基本的二叉树抽象数据类型的定义

ADT BinTree:  # 一个二叉树抽象数据类型
    BinTree(self,data, left, right)  # 构造操作，创建一个新的二叉树
    is_empty(self)  # 判断self是否为一个空二叉树
    num_nodes(self)  # 求二叉树的结点个数
    data(self)  # 获取二叉树根存储的数据
    left(self)  # 获取二叉树的左子树
    right(self)  # 获取 二叉树的右子树
    set_left(self, btree)  # 用btree取代原来的左子树
    set_right(self, btree)  # 用btree取代原来的右子树
    traversal(self)  # 遍历二叉树中各结点数据的迭代器
    forall(self, op)  # 对二叉树中的每个结点的数据执行操作op

二叉树的基本操作包括创建二叉树，判断是否是空树，子树操作，结点遍历

遍历二叉树

• 每棵二叉树右唯一的根结点，可以将其看作这棵二叉树的唯一标识，是基于树结构的处理过程的入口。二叉树中每个结点可能保存一些数据，因此也是汇集型的数据结构。
• 遍历一棵二叉树，就是按照某种系统化的方式范文二叉树里的每个结点一次，这一过程可以基于二叉树的基本操作实现，遍历中可能操作结点里的数据
• 二叉树的结构比较复杂，因此系统化遍历右多种可能的方式，下面讨论集中不同的算法：
• 深度优先遍历：顺着一条路经尽可能向前探索，必要时回溯，对于二叉树，最基本的回溯情况就是检查完一个叶结点，由于无路可走，只能回头
  • 按深度优先方式遍历一棵二叉树，需要做三件事：
    • 遍历左子树
    • 遍历右子树
    • 访问根结点
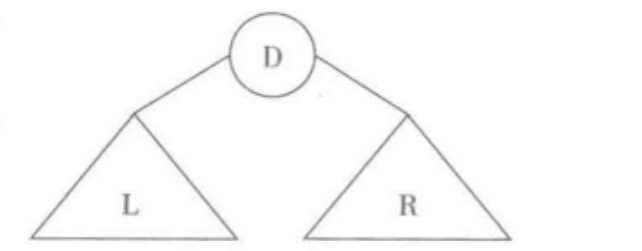
  • 下面用L、R、D表示这三项工作，如图所示，选择这三项工作的不同执行顺序，就可以得到三种常见的遍历顺序，
    • 先根序遍历---按DLR顺序
    • 中根序遍历---按LDR顺序
    • 后根序遍历---按LRD顺序
  • 
  • 在遍历过程中遇到子树为空的情况，就立即结束处理并转去继续做下一步工作，例如，在先根序中遇到左子树为空，就转去遍历相应的右子树。
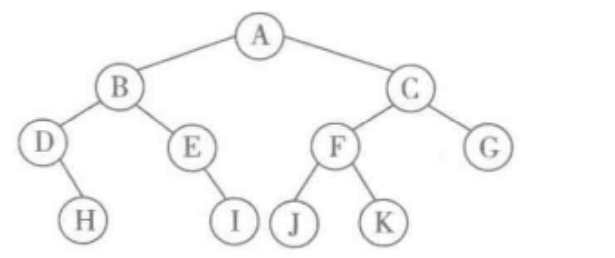
  • 例子，按不同的深度优先方式遍历下图二叉树
  • 
  • 按先根序遍历,先访问根节点，而后以同样方式顺序遍历左子树和右子树，得到的结点访问序列：ABDHEICFJKG
  • 按后根序遍历，先以同样方式遍历左右子树，最后访问根节点，得到顺序：HDIEBJKFGCA
  • 按中根序遍历，先以同样方式遍历左子树，而后 访问根节点，最后再以同样方式遍历右子树，得到的遍历序列：DHEIBAJFKCG
• 宽度优先遍历：按路径长度由近到远的访问结点，常见在每一层里都 从左到右逐个访问，上图宽度优先遍历结果为：ABCDEFGHIJK